Декларативное программирование
Языки, которые мы уже обсудили, имеют одну общую черту: базовый оператор в них - это оператор присваивания, который заставляет компьютер переместить данные из одного места в другое. Принципиально иной подход к программированию заключается в том, чтобы описывать вычисление, используя уравнения, функции, логические выводы и т. п. Особое внимание в декларативном программировании уделяется тому, что нужно сделать, а не тому как это нужно сделать.
Мы рассмотрим особенности двух ветвей декларативного программирования: функциональное, основанное на математическом понятии функции, которая не изменяет свое окружение, в отличии от функций в процедурных языках, допускающих побочные эффекты, и логическое, в котором программы выражены в виде формул математической логики и компьютер для решения задачи пытается вывести логические следствия из них.
Функциональная программа состоит из совокупности определений функций, которые в свою очередь представляют собой вызовы других функций и предложений, управляющих последовательностью вызовов. При этом функции часто либо прямо, либо опосредованно вызывают сами себя (рекурсия).
Каждая функция возвращает некоторое значение в вызвавшую его функцию, вычисление которой после этого продолжается; этот процесс повторяется до тех пор, пока начавшая процесс вычислений функция не вернет конечный результат пользователю.
"Чистое" функциональное программирование не содержит оператора присваивания, в нем вычисление любой функции не приводит ни к каким побочным эффектам, отличным от собственно вычисления ее значения. Разветвление вычислений основано на механизме обработке аргументов условного предложения, а циклические вычисления реализуются с помощью рекурсии.
Отсутствие оператора присваивания делает переменные, используемые в функциональных языках программирования, очень похожими на переменные в математике - получив однажды свои значения, они больше никогда их не меняют. Отсутствие побочных эффектов в процессе вычисления функций приводит к тому, что порядок выполнения отдельных фрагментов программы не существенен - итоговое значение в любом случае будет одинаковым.
Функциональное программирование весьма красиво и иногда в качестве первого языка программирования, изучаемого студентами, выбирается Haskell или Lisp. Для успешного овладения данным стилем программирования, впрочем, необходимо весьма глубокое понимание многих разделов математики.
Пример
Хорошей иллюстрацией функционального стиля программирования является программа на языке Haskell для получения всех пифагоровых троек чисел, не превосходящих заданного числа (пифагоровой тройкой называют три целых числа, являющихся сторонами некоторого прямоугольного треугольника).
Создайте файл с именем triads.hs в который поместите следующий текст: triads n = [(x,y,z)|let ns=[1..n], x<-ns, y<-ns, z<-ns, x*x+y*y==z*z] (скачать файл triads.hs)
triads n = [(x,y,z) | let ns = [1 .. n], x <- ns, y <- ns, z <- ns, x*x+y*y == z*z]
Такую программу легко понять: получить все тройки целых чисел x, y и z, не превышающих заданного числа n и удовлетворяющих условию x2+y2=z2.
Для запуска интерпретатора языка Haskell в командной строке наберите hugs. После появления приглашения > введите команду :load triads.hs для загрузки содержимого файла в память. Теперь можно находить пифагоровы триады, например, при помощи следующего вызова функции triads 50. Для завершения работы интерпретатора наберите :quit и нажмите на клавишу Enter.
Следующая программа на языке Haskell уже не столь очевидна, но она поражает своей краткостью.
Пример
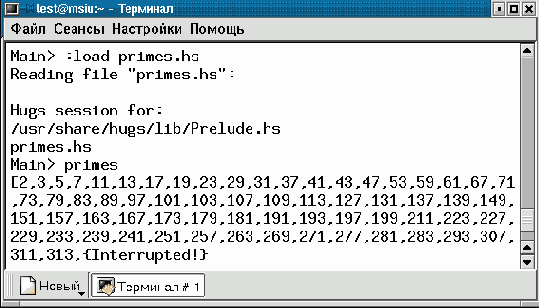
Создайте файл с именем primes.hs и поместите в него следующие строки:
-- primes :: Integral a => [a] primes = map head (iterate sieve [2..]) sieve (p:xs) = [ x | x<-xs, x `rem` p /= 0 ]
(скачать файл primes.hs)
primes = map head (iterate sieve [2 ..]) sieve (p:xs) = [ x | x <- xs, x `rem` p /= 0 ]
После старта интерпретатора hugs и загрузки в него этой программы достаточно вызвать функцию primes (без аргументов) и программа начнет печатать простые числа до тех пор, пока вы не прервете ее выполнение, нажав комбинацию клавиш Ctrl+C.
Еще одной реализацией декларативного стиля является логическое программирование, основанное на логике предикатов, которое подробно рассматривается в следующей главе.
Логика предикатов - это ветвь формальной логики, получившая развитие в XX веке. В логическом программировании основное внимание уделяется описанию структуры прикладной задачи, а не выработке предписаний компьютеру, что ему следует делать. Prolog (от французского PROgrammation LOGique, далее Пролог) - это наиболее известный язык логического программирования. Этот язык (наряду с функциональным языком Lisp) часто называют языком искусственного интеллекта - с его помощью решаются задачи создания экспертных систем и систем обработки естественных языков.
Пример
Для иллюстрации принципов логического программирования с использованием языка Пролог приведем программу, находящую решение известной головоломки "Ханойская башня", изобретенной французским математиком Люка в 1883 году и украшенной им же легендой.
| "Где-то в непроходимых джунглях, недалеко от города Ханоя, есть монастырь бога Брамы. В начале времен, когда Брама создавал Мир, он воздвиг в этом монастыре три высоких алмазных стержня и на один из них возложил 64 диска, сделанных из чистого золота. Он приказал монахам перенести эту башню на другой стержень (в соответствии с правилами, разумеется). С этого времени монахи работают день и ночь. Когда они закончат свой труд, наступит конец света." |
Поместите в файл с именем hanoi.pl следующий текст (символ % начинает комментарий, который не обязательно помещать в файл).
% move(число_дисков, откуда, куда, через) move(1,X,Y,_) :- write('Move top disk from '), %передвиньте верхний диск с write(X), write(' to '), write(Y), nl. move(N,X,Y,Z) :- N>1, M is N-1, move(M,X,Z,Y), move(1,X,Y,_), move(M,Z,Y,X).
(скачать файл hanoi.pl)
% move(число_дисков, откуда, куда, через) move(1,X,Y,_) :- write('Move top disk from '), write(X), write(' to '), write(Y), nl. move(N,X,Y,Z) :- N>1, M is N-1, move(M,X,Z,Y), move(1,X,Y,_), move(M,Z,Y,X).
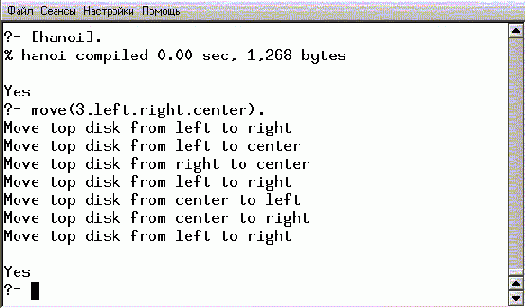
Запустите интерпретатор языка Пролог при помощи команды pl. После появления приглашения к работе (?- ) загрузите содержимое файла командой [hanoi]. (расширение файла указывать не нужно, а вот точка после закрывающей квадратной скобки необходима). Теперь, чтобы заставить Пролог решить задачу о перемещении трех дисков, введите следующий запрос:
move(3,left,right,center).
(не забудьте о точке в конце ввода). Ниже приводится порядок перемещения дисков, найденный этой программой.
Для завершения работы с интерпретатором наберите команду halt. и нажмите Enter.
Задания
Измените программу triads.hs так, чтобы не выводились одинаковые тройки чисел, такие как (3,4,5) и (4,3,5). Для этого введите дополнительное условие, например, x<y.Получите решение головоломки "Ханойская башня" для четырех дисков.
Директивное программирование
Директивное программирование - один из наиболее естественных для человека подходов к написанию программ. Ведь программа в этом случае состоит из операторов присваивания и предложений, управляющих последовательностью их выполнения. При написании подобной программы необходимо найти такую цепочку команд, которая приведет в конце концов к вычислению (и, возможно, печати) одной или нескольких искомых величин.
Директивное программирование стали называть процедурным, когда в процессе увеличения сложности моделируемых систем и размера получаемых программ возникла концепция подпрограмм, называемых также процедурами (procedure), функциями (function) или методами (method). Подпрограмма позволяет локализовать в ней процесс выполнения определенного действия, которое может быть повторено многократно с помощью механизма вызова.
При этом исходная программа превращается из одной большой цепочки команд в значительно более короткую и понятную последовательность вызовов подпрограмм, решающих более простые подзадачи. При вызове подпрограммы ей часто передают так называемые параметры, а она после завершения своей работы обычно возвращает некоторый результат. Механизмы передачи параметров в различных языках программирования сильно отличаются друг от друга.
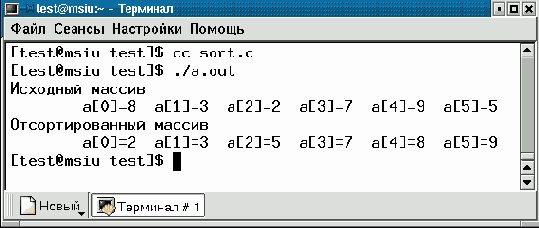
Ниже приводится пример программы на языке C, в которой кроме главной функции main используются еще две подпрограммы - print_array, печатающая элементы переданного ей массива целых чисел, и selection, сортирующая массив, переданный ей в качестве аргумента.
#include <stdio.h>
void print_array(int c[], int n, char* t) { int i; printf("%s",t); for (i = 0; i < n; i += 1) printf("ta[%d]=%d", i, c[i]); printf("\n"); }
void selection(int c[], int n) { int i, j, k, x;
for (i = 0; i < n; i += 1) { for (x = c[k=i], j = i + 1; j < n; j++) if (c[j] < x) x = c[k=j]; c[k] = c[i]; c[i] = x; } }
int main(void) { int a[] = {8, 3, 2, 7, 9, 5};
int n = sizeof(a)/sizeof(int); print_array(a, n, "Исходный массив\n"); selection(a, n); print_array(a, n, "Отсортированный массив\n"); return 0; }
Разместите текст этой программы в файле с именем sort.c и выполните следующие команды, компилирующие и запускающие ее:
cc sort.c ./a.out
Функция main дважды вызывает процедуру print_array: сначала для печати исходного массива, а затем, после вызова функции selection, для печати его же в уже отсортированном виде. Однажды реализованные функции print_array и selection могут быть использованы при написании относительно большой программы многократно.
Для того чтобы программа была понятной, подпрограммы не должны быть слишком большими. Увеличение числа подпрограмм тоже ведет к значительному росту сложности программы в целом и, как следствие, к снижению ее надежности. Отсюда следует вывод: написать большую правильно работающую программу, используя классическое процедурное программирование практически невозможно.
Со временем при проектировании программ акцент сместился с организации процедур на организацию структур данных. Современные директивные языки программирования предлагают еще один метод структурирования программ: инкапсуляция (от слова capsule - капсула, контейнер) данных и подпрограмм в более крупные объекты, называемые модулями. Большую часть данных модуля и выполняемые операторы можно скрыть таким образом, что их нельзя будет изменить или использовать способами, отличными от заранее предопределенных. Эта парадигма известна, как принцип сокрытия данных. Если в языке нет возможности сгруппировать процедуры вместе с данными, то он плохо поддерживает модульный стиль программирования.
Типичный пример модуля - реализация структуры данных, называемой стеком. Стек можно уподобить коробке с листами бумаги. Новый лист кладется в стопку поверх остальных. Только верхний лист может быть прочитан или извлечен из коробки. Для того чтобы извлечь некоторый лист из коробки, необходимо сначала вынуть все те, что лежат над ним.
Стек функционирует точно также, только в нем хранится совокупность произвольных элементов. Новый элемент помещается на вершину стека с помощью операции втолкнуть (push).
Виден в стеке только самый верхний элемент, который может быть извлечен из него командой вытолкнуть (pop). Иногда говорят, что стек задает дисциплину обслуживания LIFO (Last In First Out - последним пришел, первым выйдешь). Организация данных в виде стека широко распространена в программировании. Например, управление автоматически распределяемой памятью в процессе выполнения программы производится по принципу стека.
При модульном подходе задача сначала разбивается на подзадачи и осуществляется реализация этих подзадач, а затем эти подзадачи комбинируются друг с другом для решения основной задачи. Программа, реализующая работу со стеком, написанная в модульном стиле, не позволит пользователю добраться до внутреннего представления данных стека. Доступ к его элементам будет возможен только с помощью методов push и pop.
Способность языка поддерживать модули не помогает разработчику оптимально разбить программу на модули. В то же время именно от качества декомпозиции и способности разработчика программы выбрать наиболее подходящую структуру для ее реализации зависит качество всей системы. Объектно-ориентированное программирование, с которым мы познакомимся чуть позже, предлагает принципиально иной подход к решению данной проблемы.
Клеточные автоматы
Моделирование событий реального мира может производиться многими способами. Явления макромира достаточно хорошо описываются моделями, построенными на математике бесконечного и непрерывного. События же, происходящие в микромире, плохо поддаются описанию подобным способом и требуют применения других принципов моделирования.
Еще в 1970 году А.Н. Колмогоровым давался прогноз, что с "развитием современной вычислительной техники будет во многих случаях разумно изучение реальных явлений вести, избегая промежуточный этап их стилизации в духе математики бесконечного и непрерывного, переходя прямо к дискретным моделям". Сейчас уже можно с уверенностью сказать, что этот прогноз сбылся, так как появилось большое количество разнообразных математических систем, основанных на принципе мелкозернистого параллелизма, и, самое главное, появились программные и аппаратные комплексы, способные моделировать работу таких систем.
Основной отличительной особенностью систем с мелкозернистым параллелизмом является возможность одновременного (параллельного) изменения состояния всей системы, в то время как каждый участок системы взаимодействует только со своими непосредственными соседями. Это свойство позволяет при моделировании связать события, происходящие на микроуровне, с изменениями макроуровневого моделируемого объекта.
Классической системой с мелкозернистым параллелизмом является клеточный автомат, а игра Джона Конвея "Жизнь" - типичный пример клеточного автомата, представляющего собой дискретную динамическую систему. Клеточные автоматы фактически являются синтетическими мирами, поведение которых определяется простыми локально действующими правилами. В этих мирах пространство представляет собой равномерную сетку, каждая ячейка которой (клетка) содержит информацию о своем состоянии. Изменение времени происходит дискретно, а законы такого мира представляют собой небольшое количество правил, основные из которых описываются таблицей переходов, по которой клетка вычисляет свое новое состояние на каждом такте (минимальный отрезок времени) на основе своего состояния и состояний ее соседей.
Если состояние системы в произвольный момент времени характеризуется лишь ее предыдущим состоянием и набором правил, регламентирующих ее переход, то она называется автоматом. Клеточные автоматы широко применяются для моделирования систем, в которых важную роль играет пространственное взаимодействие между элементами. Существует много примеров таких моделей в биологии, информатике (включая системы телекоммуникации) и других областях. В физике, например, клеточные автоматы применяются для анализа явлений переноса (теплопроводности, диффузии и вязкости) и моделирования твердого тела.
Познакомимся подробнее с игрой "Жизнь", относящейся к категории так называемых моделирующих игр - игр, которые в той или иной степени имитируют процессы, происходящие в реальной жизни. Жизнь, как естественный процесс - явление настолько сложное и увлекательное, что тысячи ученых пытались раскрыть ее тайны. Свой вклад в решение этой проблемы внес и человек, не имевший к биологии никакого отношения, английский математик Джон Хортон Конвей.
Возникающие в процессе придуманной им игры ситуации очень похожи на реальные процессы, происходящие при зарождении, развитии и гибели колонии живых организмов. Они рождаются при благоприятном сочетании соответствующих факторов и умирают, когда условия их существования становятся невыносимыми. Условия рождения и смерти определяются исключительно взаимным расположением участников.
Действие игры происходит на плоскости, разделенной на клетки. Каждая клетка окружена 8 такими же клетками (так называемая окрестность Мура) и может находиться в двух состояниях - живом или мертвом (быть пустой). Гибель и рождение всех организмов происходит одновременно. На состояние любой клетки оказывают влияние только состояния соседних с ней клеток. Во времени эти состояния дискретно изменяются в соответствии со следующими правилами (генетическими законами Конвея).
Выживание или гибель. Если живая клетка имеет менее 2 или более 3 соседей в окрестности из 8 клеток, то в следующем поколении она умирает (моделирование реальных условий - недостатка питания или перенаселенности), в противном случае она выживает.Рождение.
В пустой клетке появляется новая живая клетка, если у нее ровно 3 соседа.
Основная идея игры состоит в том, чтобы, начав с некоторого расположения живых клеток, проследить за ее эволюцией. Популяция клеток постоянно претерпевает необычные изменения. Иногда колония клеток постепенно вымирает, однако произойти это может не сразу, а лишь после того, как сменится очень много поколений.
В большинстве своем исходные конфигурации либо переходят в устойчивые и перестают изменяться, либо навсегда переходят в колебательный режим. При этом, конфигурации, не обладавшие в начале симметрией, обнаруживают тенденцию к переходу в симметричные формы, которые в процессе эволюции не утрачиваются. Три примера развития колоний показаны на рисунке.

Познать "Жизнь" на практике проще всего с помощью листа бумаги в клеточку и ручки. Можно воспользоваться также шахматной доской и обычными шашками двух цветов. Еще проще - использовать для этой цели компьютер. Уже на заре развития компьютерной техники были написаны многочисленные программы, моделирующие "Жизнь".
За прошедшие годы исследований было выявлено большое число интересных фигур, например, такая конструкция, как "часы", которая содержит внутри нечто похожее на стрелку. От шага к шагу эта стрелка поворачивается на 90 градусов, создавая иллюзию вращения ее по кругу.
Планер (glider) - это самый ранний из обнаруженных и наиболее примечательный объект, одной из особенностей которого является его способность спонтанно возникать в совершенно произвольных ситуациях и перемещаться за пределы видимого пространства (в случае, когда движение направлено в противоположную сторону от сосредоточения основных объектов популяции). Через определенное количество шагов планеры покидают пределы освоенной области и устремляются в "космические дали".

Более подробную информацию о игре "Жизнь" и программы для наблюдения за эволюцией объектов можно найти по следующему URL: elvisti.kiev.ua/skl/conwey1/w_life_n.htm.
Как уже было сказано, игра "Жизнь" описывается с помощью теории автоматов. На основе этого примера можно сформулировать общие правила построения клеточных автоматов.
Состояние клеток дискретно (обычно 0 и 1, хотя могут быть автоматы и с большим числом состояний).Соседями является ограниченное число клеток, часто это ближайшие клетки.Правила, задающие динамику развития клеточного автомата, обычно имеют простую функциональную форму и зависят от решаемой проблемы.Клеточный автомат является тактируемой системой, т. е. смена состояний клеток происходит одновременно.Клеточные автоматы предоставляют большую свободу в выборе структуры и правил развития системы. Это позволяет моделировать на их основе и решать с их помощью самые разнообразные задачи.
Представим себе некую исходную фигуру на плоскости, к которой начинают применяться правила "Жизни". В результате эволюции возникнут сотни, а в отдельных случаях и тысячи разнообразнейших (на первый взгляд не связанных друг с другом) фигур. Но достаточно лишь знать начальное расположение элементов и номер шага, чтобы восстановить нужную фигуру. По-видимому, эта идея может быть использована для построения новых алгоритмов сжатия информации.
Возникающие в процессе эволюции узоры могут найти применение в различных областях, где необходимы сложные замысловатые изображения, например, для оформительских картинок, ткацких узоров, компьютерного дизайна. Особенно интересные результаты можно получить при присвоении различным элементам собственных цветов (например, в зависимости от возраста элемента).
Задания
Постройте модель процесса распространения инфекции стригущего лишая по участку кожи размером n x n (n-нечетное) клеток. Заражение начинается с центральной клетки. В каждый интервал времени пораженная инфекцией клетка может с вероятностью 1/2 заразить любую из соседних здоровых клеток. Через шесть единиц времени зараженная клетка становится невосприимчивой к инфекции. Возникший иммунитет действует в течение последующих четырех единиц времени, а затем клетка выздоравливает.
В ходе компьютерного эксперимента выдавайте текущее состояние моделируемого участка кожи, отмечая зараженные, невосприимчивые к инфекции и здоровые клетки.
Разработайте имитационную модель системы "хищник-жертва" по следующей схеме. Остров размером 20x20 заселен дикими кроликами, волками и волчицами. Имеется несколько представителей каждого вида. Кролики довольно глупы: в каждый момент времени они с одинаковой вероятностью 1/9 передвигаются в один из восьми соседних квадратов (за исключением участков, ограниченных береговой линией) или просто сидят неподвижно. Каждый кролик с вероятностью 0,2 превращается в 2 кроликов. Волчицы передвигаются случайным образом до тех пор, пока в одном из соседних восьми квадратов не окажется кролик. Если волчица и кролик оказываются в одном квадрате, волчица съедает кролика и получает одно очко, в противном случае она теряет 0,1 очка за каждую единицу времени. Волки и волчицы с нулевым количеством очков умирают. В начальный момент времени все волки и волчицы имеют 1 очко. Волк ведет себя подобно волчице до тех пор, пока в соседних квадратах не исчезнут все кролики; в этом случае, если волчица находится в одном из восьми ближайших квадратов, волк гонится за ней. Если волк и волчица окажутся в одном квадрате, они производят потомство случайного пола. Проследите, как сказываются на эволюции популяции изменение различных параметров модели.
Компьютерное моделирование
Компьютерная модель - это модель реального процесса или явления, реализованная компьютерными средствами. Если состояние системы меняется со временем, то модели называют динамическими, в противном случае - статическими.
Процессы в системе могут протекать по-разному в зависимости от условий, в которых находится система. Следить за поведением реальной системы при различных условиях бывает трудно, а иногда и невозможно. В таких случаях, построив модель, можно многократно возвращаться к начальному состоянию и наблюдать за ее поведением. Этот метод исследования систем называется имитационным моделированием.
Примером имитационного моделирование может служить вычисление числа

Теоретическая основа этого метода была известна давно, однако до появления компьютеров этот метод не мог найти сколько-нибудь широкого применения, ибо моделировать случайные величины вручную - очень трудоемкая работа. Название метода происходит от города Монте-Карло в княжестве Монако, знаменитого своими игорными домами, ибо одним из механических приборов для получения случайных величин является рулетка.
Следует заметить, что данный метод вычисления площади круга будет давать корректный результат только если точки будут не просто случайно, но еще и равномерно разбросанными по всему квадрату. Для моделирования равномерно распределенных в интервале от 0 до 1 случайных чисел используется датчик случайных чисел - специальная компьютерная программа. На самом деле эти числа определяются по некоторому алгоритму и уже в силу этого они не являются вполне случайными.
Получаемые таком способом числа часто называют псевдослучайными. Вопрос о качестве датчиков случайных чисел весьма непрост, однако для решения не слишком сложных задач обычно достаточно возможностей датчиков, встроенных в большинство систем программирования и электронных таблиц.
Заметим, что располагая датчиком равномерно распределенных случайных чисел, генерирующим числа r из интервала [0; 1), легко получить равномерно распределенные случайные числа на произвольном интервале [a; b) по формуле
x=a+(b-a)*r.
Задания
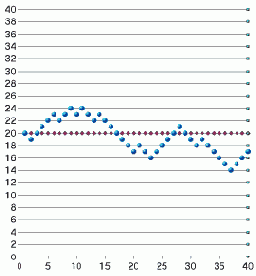
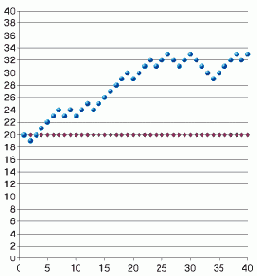
Разработайте модель случайного одномерного блуждания (модель "пьяницы"). Блуждание задается по правилу: если случайное число из отрезка [0;1) меньше 0,5, то делается шаг влево, в противном случае - вправо.
Для реализации модели используйте электронную таблицу. Предположим, что в начальный момент объект наблюдения находится в точке с y-координатой равной y0. Если случайное число больше 0,5, то y-координата увеличивается на 1, в противном случае - уменьшается на 1.
Для наглядности процесса блуждания постройте диаграмму, отражающую местоположение объекта. При пересчете таблицы датчики выдадут новые последовательности чисел и траектория блуждания изменится.
На рисунках приведены две случайные траектории блуждания, вдоль горизонтальной оси отложено число шагов.
Моделирование
В 1870 г. английское Адмиралтейство спустило на воду новый броненосец "Кэптен". Корабль вышел в море и перевернулся. Погиб корабль и все находящиеся на нем люди. Это было совершенно неожиданно для всех, кроме английского ученого-кораблестроителя В. Рида, который предварительно провел исследования на модели броненосца и установил, что корабль опрокинется даже при небольшом волнении. Но ученому, проделывающему, как казалось, несерьезные опыты с "игрушкой", не поверили лорды из Адмиралтейства. И случилось непоправимое...
Модели и моделирование используются человечеством давно. С помощью моделей и модельных отношений развились разговорные языки, письменность, графика. Наскальные изображения наших предков, затем картины и книги - это модельные, информационные формы передачи знаний об окружающем мире последующим поколениям. Модели применяются при изучении сложных явлений, процессов, конструировании новых сооружений. Хорошо построенная модель, как правило, доступнее для исследования, нежели реальный объект. Более того, некоторые объекты вообще не могут быть изучены непосредственным образом: недопустимы, например, эксперименты с экономикой страны в познавательных целях; принципиально неосуществимы эксперименты с прошлым или, скажем, с планетами Солнечной системы и т. п.
Модель позволяет научиться правильно работать с объектом, апробируя различные варианты управления на его модели. Экспериментировать в этих целях с реальным объектом в лучшем случае бывает неудобно, а зачастую просто вредно или вообще невозможно в силу ряда причин (большой продолжительности эксперимента во времени, риска привести объект в нежелательное и необратимое состояние и т. п.)
| Модель - это материальный или мысленно представляемый объект, замещающий в процессе изучения объект-оригинал, и сохраняющий значимые для данного исследования типичные его черты. Процесс построения модели называется моделированием. |
Другими словами, моделирование - это процесс изучения строения и свойств оригинала с помощью модели.
Приведем одну из возможных классификаций моделей.
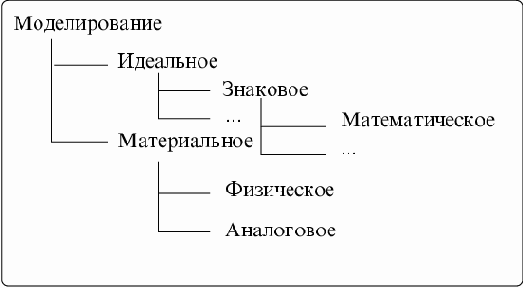
Различают материальное и идеальное моделирование. Материальное моделирование, в свою очередь, делится на физическое и аналоговое моделирование.
Физическим принято называть моделирование, при котором реальному объекту противопоставляется его увеличенная или уменьшенная копия, допускающая исследование (как правило, в лабораторных условиях) с помощью последующего перенесения свойств изучаемых процессов и явлений с модели на объект на основе теории подобия. Примерами моделей такого рода служат: в астрономии - планетарий, в архитектуре - макеты зданий, в самолетостроении - модели летательных аппаратов и т. п.
Аналоговое моделирование основано на аналогии процессов и явлений, имеющих различную физическую природу, но одинаково описываемых формально (одними и теми же математическими уравнениями).
От предметного моделирования принципиально отличается идеальное моделирование, которое основано не на материальной аналогии объекта и модели, а на аналогии идеальной, мыслимой. Основным типом идеального моделирования является знаковое моделирование.
Знаковым называется моделирование, использующее в качестве моделей знаковые преобразования какого-либо вида: схемы, графики, чертежи, формулы, наборы символов.
Важнейшим видом знакового моделирования является математическое моделирование, при котором исследование объекта осуществляется посредством модели, сформулированной на языке математики. Классическим примером математического моделирования является описание и исследование законов механики Ньютона средствами математики.
Пример
Посмотрите на следующую запись и попробуйте определить, что скрывается за этими знаками:
a1x1+b1x2=c1
a2x1+b2x2=c2
Ответы, полученные от людей, имеющих различные специальности, будут сильно различаться. Вот некоторые из возможных вариантов.
Математик: "Это система двух линейных алгебраических уравнений с двумя неизвестными, но что именно она выражает, сказать не могу".
Инженер-электрик: "Это уравнения электрического напряжения или токов с активными напряжениями".
Инженер-механик: " Это уравнения равновесия сил для системы рычагов или пружин".
Инженер-строитель: "Это уравнения, связывающие силы деформации в какой-то строительной конструкции".
Какой же из ответов правильный? Не удивляйтесь, но каждый из них в некотором смысле верен. Все зависит от того, что скрывается за постоянными коэффициентами a, b, c и символами неизвестных x1 и x2.
Схема процесса моделирования
Объект -> Модель -> Изучение модели -> Знания об объекте
Для построения моделей используют два принципа: дедуктивный (от общего к частному) и индуктивный (от частного к общему). При первом подходе рассматривается частный случай общеизвестной фундаментальной модели, которая приспосабливается к условиям моделируемого объекта с учетом конкретных обстоятельств. Второй способ предполагает выдвижение гипотез, декомпозицию сложного объекта, анализ, а затем синтез. Здесь широко используется подобие, поиск аналогий, умозаключение с целью формирования каких-либо закономерностей в виде предположений о поведении системы.
Технология моделирования требует от исследователя умения корректно формулировать проблемы и задачи, прогнозировать результаты, проводить разумные оценки, выделять главные и второстепенные факторы для построения моделей, находить аналогии и выражать их на языке математики.
В современном мире все шире применяется процесс компьютерного моделирования, подразумевающий использование вычислительной техники для проведения экспериментов с моделью.
Объектно-ориентированное программирование
Объектно-ориентированное программирование (ООП) - это результат естественной эволюции более ранних методологий программирования. Потребность в ООП связана со стремительным усложнением разрабатываемых программ и, как следствие, их недостаточной надежностью. Модульное программирование, рассмотренное выше, оказалось не способным решить эту проблему.
Практически все современные языки программирования, независимо от принадлежности к тому или иному стилю (директивному или декларативному), поддерживают концепцию ООП. Среди них C++, Java, Ruby и Haskell. Существуют и версии объектно-ориентированного Пролога.
Можно сказать, что ООП - это моделирование объектов посредством иерархически связанных классов. При этом малозначащие детали объекта скрыты от нас, и если мы даем команду какому-то объекту, то он "знает", как ее выполнить. Фундаментальной концепцией в ООП является понятие обязанности или ответственности за выполнение действия.
Все объекты являются представителями, или экземплярами, классов. Метод, активизируемый объектом в ответ на сообщение, определяется классом, к которому принадлежит получатель сообщения. Все объекты одного класса используют одни и те же методы в ответ на одинаковые сообщения.
Классы представляются в виде иерархической древовидной структуры, в которой классы с более общими чертами располагаются в корне дерева, а специализированные классы и в конечном итоге индивидумы располагаются в ветвях. На рисунке показана одна из возможных иерархий классов, включающая в себя собак Белку и Стрелку, кошку Мурку и утконоса Фросю.
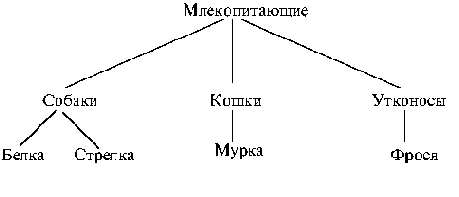
Классы собак, кошек и утконосов являются дочерними по отношению к классу млекопитающих, следовательно наследуют его свойства. При программной реализации этой иерархии логично метод "кормление детенышей" реализовывать в родительском классе, вместо того, чтобы несколько раз дублировать его в каждом из подклассов. Наследование свойств родительского класса позволяет использовать их в дочерних классах. Немного другая ситуация с рождением детенышей, ведь утконосы откладывают яйца, а не являются живородящими животными? В этой ситуации выручает свойство полиформизма: различные реализации методов могут носить одинаковые имена, а система сама определит какую из реализаций использовать в том или ином случае.
В нашем примере следует в классе млекопитающих реализовать метод "потомство" (родить детеныша), в классах собак и кошек этот метод будет отсутствовать (система будет искать его в родительском классе и найдет его там), а в классе утконосов нужно написать новый метод, с тем же именем, но другой реализацией (отложить яйца).
Итак, в основе ООП лежат три основных понятия:
инкапсуляция (сокрытие данных в классе или методе);наследование;полиморфизм.
Инкапсуляцию можно представить, как защитную оболочку вокруг кода данных, с которыми этот код работает. Оболочка задает поведение и защищает код от произвольного доступа извне.
Наследование - это процесс, в результате которого один тип наследует свойства другого типа.
Полиморфизм - это концепция, позволяющая иметь различные реализации для одного и того же метода, которые будут выбираться в зависимости от типа объекта, переданного методу при вызове.
Пример
Для иллюстрации некоторых принципов ООП приведем небольшую программу на языке Ruby, который тоже поддерживает объектно-ориентированный стиль программирования.
Поместите в файл с именем life.rb фрагмент кода, расположенный ниже.
#!/usr/bin/ruby
class Animal def breath #Дыхание print "все животные дышат: вдохнули и выдохнули\n" end end
class Cat<Animal def bark # Подать голос print "Mew Mew, я кошка. \n" end end
class Dog def bark # Подать голос print "Bow Wow, я собака. \n" end end
class Bird def lay_egg print "Яйцо снесено\n" end def fly print "Я птица, я лечу!!!\n" end end
class Penguin<Bird def fly print "Пингвины не летают!!!\n" end end
# Создаем объекты разных классов pochi = Dog.new pochi.bark
tama = Cat.new tama.breath tama.bark
macaw = Bird.new macaw.lay_egg macaw.fly
penguin = Penguin.new penguin.lay_egg penguin.fly
(скачать файл life.rb)
Для запуска этой программы выполните в окне shell команду
ruby life.rb
Если вы поняли, какой мир описывает данная программа, то попробуйте справиться с приведенными ниже заданиями.
Задания
Создайте еще одну кошку.Объясните, кем является pochi и сможет ли он выполнить команду pochi.breath (дышать)? Если нет, то внесите соответствующие изменения в текст программы.Измените код программы так, чтобы и птицы в ней тоже умели дышать.
Парадигмы программирования
По одной из классификаций языки программирования делятся на
директивные (directive), называемые также процедурными (procedural) или императивными (imperative),декларативные (declarative) языки, объектно-ориентированные (object-oriented).
К директивным языкам относятся такие классические языки программирования, как Algol, Fortran, Basic, Pascal, C. Наиболее существенными классами декларативных языков являются функциональные (functional) или аппликативные, и логические (logic) языки. К категории функциональных языков относятся, например, Lisp и Haskell. Самым известным языком логического программирования является Prolog (Пролог). Среди объектно-ориентированных языков программирования (языков ООП) отметим C++, Java, Python и Ruby.
Отложим пока обсуждение концепции ООП и поговорим о различии между первыми двумя парадигмами. Главное заключается в следующем: декларативная программа заявляет (декларирует), что должно быть достигнуто в качестве цели, а директивная предписывает, как ее достичь.
Поясним это на следующем примере. Предположим, вам надо пройти в городе из пункта А в пункт Б. Декларативная программа - это план города, в котором указаны оба пункта, плюс правила уличного движения. Руководствуясь этими правилами и планом города, курьер сам найдет путь от пункта А к пункту Б.
Директивная программа - это список команд примерно такого рода: от пункта А по ул. Садовой на север до площади Славы, оттуда по ул. Пушкина два квартала, потом повернуть направо и идти до Театрального переулка, по этому переулку налево по правой стороне до дома 20, который и есть пункт Б.
В директивной программе действия задаются явными командами, подготовленными ее составителем. Исполнитель же просто им следует. Хотя команды в различных языках директивного программирования и выглядят по-разному, все они сводятся либо к присваиванию какой-нибудь переменной некоторого значения, либо к выбору следующей команды, которая должна будет выполняться. Присваиванию может предшествовать выполнение ряда арифметических и иных операций, вычисляющих требуемое значение, а команды выбора реализуются в виде условных операторов и операторор повторения (циклов).
Для классических директивных языков характерно, что последовательность выполняемых команд совершенно однозначно определяется ее входными данными. Как говорят, поведение исполнителя императивной программы полностью детерминировано.
Декларативные программы не предписывают выполнять определенную последовательность действий, в них лишь дается разрешение совершать их. Исполнитель должен сам найти способ достижения поставленной перед ним составителем программы (программистом) цели, причем зачастую это можно сделать различными способами - детерминированность в данном случае отсутствует.
Нельзя сказать, что один язык лучше другого только потому, что в нем есть возможности, которые в другом отсутствуют. Здесь более важно не то, какими возможностями обладает язык, а то, насколько имеющиеся в нем возможности поддерживают избранный стиль программирования для решения определенного круга задач.
Арифметические выражения
В языке Пролог имеется ряд встроенных функций для вычисления арифметических выражений, некоторые из которых перечислены в таблице.
| X + Y | Сумма X и Y |
| X - Y | Разность X и Y |
| X * Y | Произведение X и Y |
| X / Y | Деление X на Y |
| X mod Y | Остаток от деления X на Y |
| X // Y | Деление нацело X на Y |
| X ** Y | Возведение X в степень Y |
| - X | Смена знака X |
| abs(X) | Абсолютная величина числа X |
| max(X,Y) | Большее из чисел X и Y |
| min(X,Y) | Меньшее из чисел X и Y |
| sqrt(X) | Квадратный корень из X |
| random(Int) | Случайное целое число в диапазоне от 0 до Int |
| sin(X) | Синус X |
| cos(X) | Косинус X |
| tan(X) | Тангенс X |
| log(X) | Натуральный логарифм (ln) числа X |
| log10(X) | Десятичный логарифм (lg) числа X |
| float(X) | Вещественное число, соответствующее целому числу X |
| pi | 3.14159 (приближенное значение числа  |
| е | 2 .71828 (приближенное значение числа е) |
Еще раз отметим, что Пролог старается скрыть различие между арифметикой целых и вещественных чисел везде, где это можно.
Для вычисления арифметических выражений в Прологе используется встроенный бинарный оператор is, который интерпретирует правый терм как арифметическое выражение, после чего унифицирует (если возможно) результат вычисления с левым термом (обычно с переменной). Приоритет выполнения арифметических операций является традиционным. Круглые скобки используются для изменения порядка вычислений. В следующих примерах переменная X унифицируется со значениями арифметических выражений:
?- X is 2.5 + 2.5. X = 5 Yes
?- X is 4/(2+1). X = 1.33333 Yes
?- X is cos(3*pi). X = -1 Yes
?- 1 is sin(pi/2). Yes
?- 1.0 is sin(pi/2). No
Поясним несколько неожиданный ответ Пролога в последнем запросе. Значение sin(pi/2) автоматически округляется предикатом is до целого значения 1, которое не удается унифицировать с вещественным числом 1.0. Предикат float заставит считать значение sin(pi/2) вещественным числом:
?- 1.0 is float( sin(pi/2)). Yes
Для сравнения арифметических выражений используется ряд операторов. Цель X > Y (больше) будет успешна, если выражение X будет соответствовать большему числу, чем выражение Y.
Аналогично используются операторы < (меньше), =< (меньше или равно), >= (больше или равно), =\= (не равно) и =:= (арифметически равный). Различия между операторами =:= и = очень существенны. Первый оператор сравнивает значения арифметических выражений, тогда как последний пытается унифицировать их.
Пример
?- 2 ** 3 =:= 3 + 5. Yes
?- 2 ** 3 = 3 + 5. No
?- 1.0 = float(sin(pi/2)). No
?- 1.0 =:= sin(pi/2). Yes
Заметьте, что цель X =:= Y будет истинна, даже если один из термов есть целое число, а другой - равное ему вещественное.
Пример
Порядок подцелей в запросе влияет на его результат:
?- X is 4+Y, Y=3. ERROR: Arguments are not sufficiently instantiated
?- Y=3, X is 4+Y. Y = 3 X = 7 Yes
В первом запросе сообщение об ошибке появилось потому, что первая подцель запроса (X is 4+Y) потерпела неудачу, т. к. в момент ее обработки невозможно вычислить выражение 4+Y.
Задание
Какой ответ выдаст интерпретатор Пролога на следующие запросы?
?- 3 is 2+1.?- X=3/2.?- X is 3/2.?- X is min(tan(pi/4), log(pi)).
Базы знаний
Как уже отмечалось, программа на языке Пролог, содержащая факты и правила, составляет базу знаний. При разработке программ на Прологе часто используют встроенные предикаты, т. е. предикаты, определяемые автоматически при инициализации интерпретатора Пролога.
Встроенные предикаты используются так же, как и определяемые пользователем предикаты. Единственное ограничение - встроенный предикат не может являться головой правила или появляться в факте.
Одним из наиболее часто используемых встроенных предикатов является предикат not/1 (отрицание). Этот предикат истиннен, если его аргумент ложен, и наоборот. Можно использовать и другую форму записи данного предиката \+.
Пример
Если мы определим правило
ложь(X) :- not(X). ложь1(X) :- \+(X).
то следующие запросы будут эквивалентны:
?- not(больше(собака, лошадь)). Yes;
?- ложь(больше(собака, лошадь)). Yes
Другим часто используемым встроенным предикатом является =/2 (унификация): =(X, Y). Этот предикат допускает более удобную форму записи X = Y. Значение этого предиката истинно, если термы X и Y удается унифицировать.
На предикат not/1 похож встроенный предикат \=, зависящий от двух аргументов. Утверждение X \= Y эквивалентно утверждению not(X = Y).
Иногда бывает полезно использовать предикаты, про которые заранее известно, истинны они или ложны. Для этих целей используют предикаты true/0 и fail/0. Предикат true всегда истинен, в то время как fail всегда ложен.
Встроенный предикат read/1 позволяет считывать термы с клавиатуры. При этом приглашение Пролога ?- меняется на |:. Вводимый терм должен обязательно заканчиваться точкой.
Пример
?- read(Name), read(Age). |: коля. 15.
Name = коля Age = 15 Yes
?- read(X), больше_2(X,Y). |: осел.
X = осел Y = собака ;
X = осел Y = обезьяна ; No
Если при обработке запросов Пролога вы пожелаете получить более подробный вывод, то для этих целей можно использовать предикат write/1. Аргументом этого предиката может являться любой допустимый терм Пролога. В случае, когда аргументом является переменная, будет напечатано ее значение.
Выполнение предиката nl/ 0 осуществляет перевод строки: последующий вывод начнется с новой строки. Предикат tab/1 выводит количество пробелов, определяемое его аргументом.
Пример
?- write('Hello World!'). Hello World! Yes
?- write('Hello'), nl, tab(5), write('World!'). Hello World! Yes
?- X = слон, write(X), nl. слон
X = слон Yes
В последнем примере сначала переменная X унифицируется с атомом слон, а затем значение переменной X, т. е. слон, выводится на экран при помощи предиката write/1. После перехода на новую строку Пролог выдает отчет об унифицированной переменной, т. е. печатает X = слон.
Большинство Пролог-систем предоставляет доступ к справочной информации при вызове предиката help/1. Примененный к терму (обычно представляющему имя встроенного предиката) он осуществляет вывод краткого описания этого терма.
Пример
?- help(write). write(+Term) Write Term to the current output, using brackets and operators where appropriate. See feature/2 for contrillong floating point output format.
write(+Stream, +Term) Write Term to Stream. Yes
И, напоследок, поговорим о комментариях. Комментарии никак не влияют на выполнение программы, но при правильном их использовании они оказываются весьма существенной частью исходного текста. Несколько удачно расположенных строк с комментариями могут оказать человеку, читающему программу, большую помощь. Пролог игнорирует произвольное число строк, заключенное между символами /* и */. Все, что находится между % и концом строки, также рассматривается как комментарий:
Пример
/* Это комментарий */
% Это тоже комментарий
Сумма цифр введенного числа равна
| максимум(X,X,X). максимум(X,Y,X):- X>Y. максимум(X,Y,Y):- X<Y. гипотенуза(X,Y,Z):- number(X), number(Y), Z is sqrt(X**2 + Y**2). мин_гип(A1,B1,A2,B2,Min):- гипотенуза(A1,B1,C1), гипотенуза(A2,B2,C2), Min is min(C1,C2). сумма(X,Y):- integer(X), X<10, Y is X. сумма(X,Y):- integer(X), X1 is X//10, сумма(X1,Y1), Z is X mod 10, Y is Y1+Z. печать_суммы:- write('Введите число (не забудьте точку в конце): '), read(X), nl, write(' Сумма цифр введенного числа равна '), сумма(X,Y), write(Y), nl. факт(1,1). факт(N,R):- integer(N), N>1, N1 is N-1, факт(N1,R1), R is N*R1. сумма_списка([],0). сумма_списка([H|T],S):- сумма_списка(T,S1), number(H), S is S1+H. |
| Пример 1.1. |
| Закрыть окно |
Факты
Программировать на Прологе - значит описывать некий мир. Программа на этом языке состоит из множества фраз, задающих взаимосвязь между термами. Каждый терм обозначает ту или иную сущность, принадлежащую миру. Один из способов описания - это задание фактов.
Факт - это утверждение о том, что соблюдается некоторое конкретное отношение. Он является безусловно верным. В разговорной речи под фактом понимается нечто вроде "Сегодня солнечно" или "Васе 10 лет". На Прологе это запишется в виде
'Сегодня солнечно'. 'Васе 10 лет'.
Если вы сохраните эти факты в файле и затем загрузите его, то можно задавать вопросы интерпретатору Пролога (напомним, что запрос вводится после приглашения Пролога, которое в большинстве версий имеет вид ?-) , например,
?- 'Сегодня солнечно'. Yes
?- 'Васе 10 лет'. Yes
?- 'Сегодня солнечно', 'Васе 10 лет'. Yes
Запятая между фактами в последнем запросе означает операцию логического и (конъюнкцию).
Такая форма записи соответствует логике высказываний, возможности которой, как уже говорилось, достаточно ограничены. Мы не можем задать, например, вопрос о том, сколько лет Васе. Гораздо удобнее использовать параметризованные факты, работу с которыми поддерживает логика предикатов. На Прологе факт может быть записан в виде предиката, аргументы которого являются символьными или числовыми константами.
В общем случае предикат - это логическая функция от одного или нескольких аргументов, то есть функция, действующая в множество из двух значений: истина и ложь. Предикат Пролога записывается в виде составного терма:
имя_предиката(аргументы).
Аргументы перечисляются через запятую и представляют собой какие-то объекты или свойства объектов, а имя предиката обозначает связь или отношение между аргументами. Предикат однозначно определяется парой: имя и количество аргументов. Два предиката с одинаковым именем, но различным количеством аргументов, считаются различными. Количество параметров предиката называется его арностью (arity). При описании предиката арность указывают после его имени, разделяя их символом '/' (слэш).
Как правило, имена предикатов и аргументов записываются в именительном падеже. Пробелы в них не допускаются, поэтому в качестве разделителей в символьных константах используется символ подчеркивания.
Пример
Факт "Коля работает слесарем" на Прологе запишется следующим образом:
профессия(коля, слесарь).
Здесь предикат профессия/2 имеет два аргумента: первый означает имя человека, а второй - профессию. Факт "Борису 10 лет" можно представить в виде:
возраст("Борис", 10).
Порядок аргументов предиката связан со смыслом факта и поэтому не изменяем. При записи фактов надо помнить, что:
имя факта начинается со строчной буквы; запись каждого факта заканчивается точкой.
В приведенных выше примерах профессия/2 и возраст/2 - предикаты (составные термы), коля и слесарь - атомы, 10 - число, "Борис" - строка. Подробнее о видах термов Пролога рассказывается в следующем разделе.
База данных на Прологе - это совокупность фактов. В процессе работы в базу данных можно добавлять новые факты, удалять или изменять старые.
Пример
Составим базу данных из следующих фактов: "слон больше, чем лошадь", "лошадь больше, чем осел", "осел больше, чем собака" и "осел больше, чем обезьяна":
больше(слон, лошадь). больше(лошадь, осел). больше(осел, собака). больше(осел, обезьяна).
Мы использовали предикат больше/2, имеющий два параметра.
Сохраним эту базу данных в текстовом файле и затем познакомим Пролог с ней. Теперь можно формулировать запросы к интерпретатору Пролога:
?- больше(слон, лошадь). Yes
?- больше(лошадь, слон). No
Задания
Сохраните базу данных "Цвет" в файле task1.pl: цвет(машина, красный). цвет(светофор, зеленый). цвет(солнце, желтый). цвет(море, синий).
Сформулируйте несколько запросов к данной базе данных.
Постройте базу данных из следующих фактов, используя предикат признак/2. Признак зимы - снег.Признак весны - капель.Признак лета - солнце.Признак осени - дождь.
Сохраните ее в том же файле и сформулируйте несколько запросов к данной базе данных.
женщина(анна).
| ||||||||||||||||||
| Закрыть окно |
Классическая логика и язык Пролог
Логические языки, как и следует из их названия, для цели передачи смысла программ используют средства математической логики. Сама по себе логика была изобретена как инструмент человеческой мысли, позволяющий упорядочить знания и получить из них соответствующие выводы. Поэтому идея использования принципов математической логики при составлении компьютерных программ кажется довольно естественной.
Ранее мы уже познакомились с частью логики, называемой исчислением высказываний. Но исчисление высказываний не дает возможности выразить многие факты и рассуждения, которыми пользуются в обыденной жизни. Например, рассмотрим классическое рассуждение:
Все люди смертны (p); Сократ - человек (q); следовательно, (->) Сократ смертен (r).
Это рассуждение верное, но его невозможно доказать в рамках теории высказываний. Мы можем записать формулу (p&&q)->r, но доказать ее истинность уже не сможем. Таким образом, логика высказываний не позволяет достаточно точно выразить рассматриваемое рассуждение. Это связано с тем, что она рассматривает каждое высказывание как неделимый объект, в то время как многие из высказываний зависят от неких параметров.
Исчисление предикатов является обобщением исчисления высказываний, позволяющим использовать параметры (называемые также аргументами или переменными) в высказываниях. В терминах теории предикатов наше рассуждение можно записать так:
Для всех x, если x является человеком, то x является смертным; Сократ является человеком; (следовательно) Сократ является смертным.
Изучение исчисления предикатов не является нашей задачей, однако, для того, чтобы применять язык логического программирования, не обязательно знать логику предикатов: она уже встроена в него. Достаточно изучить сам язык и привыкнуть к его выразительным средствам.
Язык Пролог, самый известный из представителей семейства языков логического программирования, вырос из работ Алана Колмерауэра (A. Colmerauer) по обработке естественного языка и независимых работ Роберта Ковальского (R.
Kowalski) по приложениям логики к программированию. Дэвиду Уоррену (D. Warren) и его коллегам из Эдинбургского университета удалось осуществить достаточно эффективную реализацию Пролога. Имя Уоррена вошло в историю логического программирования. В его честь названа базовая техника реализации Пролога, получившая название абстрактной машины Уоррена.
Программа на языке Пролог представляет собой набор фактов и (возможно) правил. Если программа содержит только факты, то ее называют база данных. Если она содержит еще и правила, то часто используют термин база знаний.
Для запуска Пролога, наберите в командной строке pl и нажмите Enter. На экране появится приглашение для ввода запросов:
?-
Запрос (вопрос) вводится после приглашения и обязательно заканчивается точкой, например,
?- 5+4<3. No
Пролог анализирует запрос и выдает ответ Yes (Да) в случае истинности утверждения и No (Нет) в противном случае или когда ответ не может быть найден.
Хранят программы на языке Пролог в текстовых файлах, чаще всего имеющих расширение pl, например, example1.pl. Для того чтобы Пролог мог оперировать информацией, содержащейся в файле, он должен ознакомится с его содержимым (проконсультироваться с ним). Это можно сделать несколькими способами. При использовании первого варианта в квадратных скобках записывается имя файла (без pl), например,
?- [example1].
В случае удачного завершения этой операции будет выдано сообщение, аналогичное следующему:
% example1 compiled 0.00 sec, 612 bytes Yes
В противном случае будет выдан список ошибок (ERROR) и/или предупреждений (Warning).
Второй способ состоит в вызове встроенного предиката consult, которому в качестве аргумента передается имя файла (также без расширения), например:
?- consult(example1).
Расширение pl часто используется для файлов, содержащих программы на языке программирования Perl, поэтому можно встретить и другие расширения для файлов с программами на Прологе. Для загрузки файлов с расширениями, отличными от pl, все имя файла следует обязательно заключать в апострофы:
?- consult('example2.prolog'). ?- ['example2.prolog'].
Обе эти команды добавляют факты и правила из указанного файла в базу данных Пролога. Можно загружать несколько файлов одновременно. В этом случае они перечисляются через запятую, например,
?- [example1, 'example2.prolog'].
Важно помнить, что все запросы должны заканчиваться точкой. Если вы забудете ее поставить, то Пролог выведет символ '|' и будет ожидать дальнейшего ввода. В этом случае надо ввести точку и нажать клавишу Enter:
?- [example1] | . Yes
Правила
Кроме фактов программы на языке Пролог могут содержать правила, позволяющие получать дополнительные знания о том мире, который описывает программа. Правило задает новый предикат через определенные ранее.
Правило состоит из головы (предиката) и тела (последовательности предикатов, разделенных запятыми). Голова и тело разделены знаком :- и, подобно каждой фразе Пролога, правило должно заканчиваться точкой. Запятая в теле правила означает конъюнкцию (&&, логическое и).
Знак :- есть схематическая запись стрелки (<-) и показывает, что из правой части следует левая. Этот знак читается как "если". Интуитивный смысл правила состоит в том, что цель, являющаяся головой, будет истинной, если Пролог сможет показать, что все выражения (подцели) в теле правила являются истинными.
Пример
Правило, определяющее отношение ребенок/2 через отношение отец/2, запишется следующим образом:
ребенок(X, Y) :- отец(Y, X).
Это означает, что если человек Y является для человека X отцом, то X является ребенком Y. Здесь X и Y - переменные. Напомним, что запись ребенок/2 показывает, что предикат ребенок является функцией от двух аргументов.
Пример
Определим отношение мать/2 через отношения родитель/2 и женщина/1 следующим образом: матерью X для человека Y является его родитель женского рода.
мать(X, Y) :- родитель(X, Y), женщина(X).
Предикаты отличаются друг от друга не только именем, но и количеством аргументов. Можно, например, определить отношение мать/1 следующим образом:
мать(X) :- родитель(X, _), женщина(X).
Так как нам в данном предикате не важно, чьим родителем является данная женщина, то мы использовали анонимную переменную.
?- мать(X, Y). X=анна Y=юлия Yes
?- мать(X). X=анна Yes
Пример
Определим отношение дедушка/2:
дедушка(X, Y) :- отец(X, Z), отец(Z, Y). дедушка(X, Y) :- отец(X, Z), мать(Z, Y).
Эти правила утверждают, что дедушкой X для человека Y является отец человека Z, который в свою очередь является отцом или матерью человека Y.
Задания
Создайте файл, содержащий следующую базу данных:
(скопировать файл1)):
женщина(анна). мужчина(борис). женщина(юлия). мужчина(олег). женщина(галина). мужчина(антон). женщина(елена). мужчина(павел).
родитель(борис,павел). % кто чей родитель(анна,юлия). родитель(анна,антон). родитель(анна,борис). родитель(олег,юлия). родитель(олег,антон). родитель(олег,борис). родитель(галина,анна). родитель(галина,елена).Добавьте правила, задающее отношения отец/2, мать/2, мать/1 и дедушка/2, после чего сформулируйте запросы, определяющие всех матерей и дедушек в данной базе.Определите отношение сестра/2 через отношения родитель/2 и женщина/1.Сформулируйте правило, определяющее отношение тетя/2 через отношения родитель/2 и сестра/2.
Рассмотрим некоторые программы, демонстрирующие обработку
Рассмотрим некоторые программы, демонстрирующие обработку числовых данных. Отметим важную особенность процедур, создаваемых на языке Пролог: они, в отличии от встроенных функций, не могут появляться в арифметических выражениях. Если требуется, например, переменной R присвоить значение, равное умноженному на три большему из двух выражений X и Y, то, используя определенную ниже процедуру максимум, это можно записать так:
максимум(X,Y,Z), R is 3*Z.
(см. примеры 1.1)
Пример 1.1.
(html, txt)
Пример
Написать процедуру, вычисляющую максимум из двух чисел.
максимум(X,X,X). максимум(X,Y,X):- X>Y. максимум(X,Y,Y):- X<Y.
В предикате максимум/3 третий аргумент является максимумом из двух чисел - первого и второго его аргументов. Смысл каждого из правил данной процедуры вполне очевиден. Посмотрим на реакцию интерпретатора Пролога на запросы, содержащие данный предикат.
?- максимум(20,50,X). X = 50 Yes
?- максимум(100,50,X). X = 100 Yes
?- максимум(X,50,100). X = 100 Yes
Последний ответ показывает, что наш предикат позволяет находить ответ на вопросы типа: "Каково должно быть число, чтобы максимум из искомого числа и числа 50 равнялся бы 100?".
Как вы думаете, почему был получен ответ "No" на следующий запрос?
?- максимум(X,50,40). No
Пример
Составьте процедуру гипотенуза/3, которая по двум катетам прямоугольного треугольника вычисляет его гипотенузу.
Воспользуемся теоремой Пифагора и встроенной функцией sqrt для вычисления квадратного корня:
гипотенуза(X,Y,Z):- Z is sqrt(X**2 + Y**2).
Программа корректно вычисляет гипотенузу, но если мы попробуем при ее помощи найти один из катетов, то убедимся, что процедура работает не вполне правильно. Чтобы избежать этого добавим проверку того, что первые два аргумента предиката - положительные числа, для чего используем встроенный предикат number/1 и сравнение с нулем:
гипотенуза(X,Y,Z):- number(X), X>0, number(Y), Y>0, Z is sqrt(X**2 + Y**2).
?- гипотенуза(3,4,X). X = 5 Yes
?- гипотенуза(3,'a',X).
No
?- гипотенуза(3,X,5). No
Пример
Напишите предикат, который по двум парам чисел - длинам катетов прямоугольных треугольников - определяет величину меньшей из гипотенуз.
Воспользуемся процедурой гипотенуза/3, разобранной выше, и встроенной функцией min/2:
мин_гип(A1,B1,A2,B2,Min):- гипотенуза(A1,B1,C1), гипотенуза(A2,B2,C2), Min is min(C1,C2).
Запросы к интерпретатору Пролога могут выглядеть так:
?- мин_гип(3,4,8,6,X). X = 5 Yes
?- мин_гип(3,4,Y,6,X). No
Пример
Факториалом натурального числа n называют произведение всех целых чисел от 1 до n включительно. Для записи факториала числа n используют обозначение n!.
| n!=n*(n-1)*(n-2)*...*2*1=n*(n-1)! |
Следующая процедура вычисляет факториал числа. Обратите внимание на использование рекурсии в данной процедуре:
факториал(1,1). факториал(N,R):- integer(N), N>1, N1 is N-1, факториал(N1,R1), R is N*R1.
Первое правило (так называемый терминальный случай, то есть тот момент выполнения процедуры, когда она перестает вызывать сама себя) гласит, что факториал единицы равен единице. Второе правило есть просто запись определения факториала: результат R получается умножением числа N на факториал числа, на единицу меньшего. Оно будет срабатывать при всех n>1 потому, что интерпретатор Пролога просматривает базу данных сверху вниз и переходит к следующему правилу или факту только в том случае, когда он не может выполнить текущее правило.
Пример
Напишите программу на языке Пролог, печатающую сумму всех цифр введенного с клавиатуры числа.
Для решения данной задачи воспользуемся двумя предикатами. Предикат сумма/2 имеет своим первым аргументом число, сумма цифр которого является его вторым аргументом. Второй предикат - печать_суммы/0- запрашивает число, вызывает предикат сумма/2 и печатает полученный результат.
сумма(X,Y):- integer(X), X<10, Y is X. сумма(X,Y):- integer(X), X1 is X//10, сумма(X1,Y1), Z is X mod 10, Y is Y1+Z.
печать_суммы:- write('Введите число (в конце точка): '), read(X), nl, сумма(X,Y), write('Сумма цифр числа '), write(X), write(' равна '), write(Y), nl.
Правило печать_суммы не имеет аргументов, данные вводятся с клавиатуры и затем, при помощи механизма унификации, передаются другим подцелям данного правила.
Пример
Напишите программу на языке Пролог, вводящую с клавиатуры два числа - координаты точки на плоскости и определяющую, попадает ли данная точка в круг единичного радиуса с центром в начале координат.
inside(X,Y,попадает):- number(X), number(Y), X**2+Y**2=<1. inside(X,Y,не_попадает):-number(X), number(Y), X**2+Y**2>1.
/* Ввести два числа и вызвать предикат inside/3 */
input:-write('Введите x-координату: '), read(X), nl, write('Введите y-координату: '), read(Y), nl, inside(X,Y,R), write(R).
Задание
Напишите процедуры на языке Пролог для решения следующих задач и приведите примеры использования этих процедур.
Измените последнюю из рассмотренных программ так, чтобы пользователь мог ввести координаты центра круга.Найдите количество цифр во введенном числе.Определите максимальную цифру введенного числа.Одноклеточная амеба каждые 3 часа делится на 2 клетки. Определите, сколько клеток будет через N часов (N=3, 6, ..., 24, т. е. кратно 3), если первоначально была одна амеба.
Рекурсивные процедуры
Рекурсия в большинстве языков программирования - это такой способ организации обработки данных, при котором программа (процедура) вызывает сама себя непосредственно, либо с помощью другой программы (процедуры).
Гравюра голландского художника Мориса Эшера "Рисующие руки" - одна из лучших иллюстраций понятия рекурсии. Всем известный стишок о попе и его собаке демонстрирует нам бесконечность рекурсивных вызовов. Используя рекурсию как прием программирования мы должны быть уверены, что рекурсивная процедура будет завершена.
В Прологе рекурсия встречается, когда предикат содержит цель, которая ссылается на саму себя. В рекурсивном правиле более сложные входные аргументы должны выражаться через менее сложные.
На примере уже имеющейся у нас базы данных объясним преимущества использования рекурсии и особенности рекурсивных правил. Пусть имеются следующие факты:
больше(слон, лошадь). больше(лошадь, осел). больше(осел, собака). больше(осел, обезьяна).
Выполним запрос к базе данных
?- больше(осел, собака). Yes
Цель больше(осел, собака) была достигнута потому, что этот факт был сообщен Прологу при загрузке базы. Теперь проверим, больше ли обезьяна слона?
Нет, не больше. Мы получили такой ответ, какой и ожидали: соответствующий запрос, а именно больше(обезьяна, слон) не подтвердился. Но, что случится, если мы зададим вопрос по-другому?
?- больше(слон, обезьяна). No
Таким образом, слоны не больше, чем обезьяны. Полученный результат совершенно не согласуется с нашими представлениями о мире, но если посмотреть на базу данных, то легко заметить, что в ней действительно ничего не сказано об отношениях между слонами и обезьянами. Однако, мы знаем, что слоны больше, чем лошади, которые в свою очередь больше, чем ослы, которые больше обезьян, поэтому слоны также должны быть больше, чем обезьяны.
Правильная интерпретация отрицательного ответа, данного Прологом, такова: информации, сообщенной системе, недостаточно для доказательства того, что слон больше обезьяны. Если мы захотим получить положительный ответ на запрос вида больше(слон, обезьяна), то мы должны обеспечить более точное описание мира.
Одним из возможных способов решения этой проблемы является добавление отсутствующих фактов, например,
больше(слон, обезьяна).
Для нашего маленького примера это означает добавление еще 5 фактов. Однако гораздо лучшим решением будет добавление в программу нового отношения, которое мы назовем больше_2. Животное X больше, чем животное Y, если это определено как факт (первое правило) или существует животное Z, для которого определен факт, что животное X больше, чем животное Z и может быть показано, что животное Z больше, чем животное Y (второе правило). На Прологе это запишется так:
больше_2(X, Y) :- больше(X, Y). больше_2(X, Y) :- больше(X, Z), больше(Z, Y).
Если в цепочке участвуют не три, а большее число объектов, то придется добавить новые правила:
больше_2(X, Y) :- больше(X, Z1), больше(Z1, Z2), больше(Z2, Y). больше_2(X, Y) :- больше(X, Z1), больше(Z1, Z2), больше(Z2, Z3), больше(Z3, Y). ...
Эта программа длинна и работать будет далеко не всегда. Она сможет просматривать базу данных только до определенной глубины, задаваемой максимальным количеством подцелей в правилах.
Поэтому воспользуемся более корректной и элегантной формулировкой. Ключевая идея здесь - определить отношение больше_2 с помощью его самого. Теперь второе (и последнее!) правило выглядит так:
больше_2(X, Y) :- больше(X, Z), больше_2(Z, Y).
Таким образом, итоговая программа будет иметь вид
больше_2(X, Y) :- больше(X, Y). больше_2(X, Y) :- больше(X, Z), больше_2(Z, Y).
Обратите внимание на порядок подцелей во втором правиле: если их поменять местами, то в большинстве реализаций языка Пролог выполнение запроса к такой базе знаний приведет к сообщению об ошибке, аналогичному следующему:
ERROR: Out of local stack
Если теперь в запросе использовать предикат больше_2 вместо больше, то программа будет работать так, как и предполагалось:
?- больше_2(слон, обезьяна). Yes
Интерпретатор всегда просматривает базу данных сверху вниз. Поэтому он анализирует сначала первую фразу процедуры больше_2 и пытается унифицировать каждый аргумент запроса с соответствующим аргументом этой фразы.
Это происходит при помощи сравнения запроса с началом правила больше_2(X, Y) (т. е. с его головой). После этого двум переменным присваиваются значения: X = слон и Y = обезьяна.
После конкретизации переменной некоторым термом это значение "закрепляется" за всеми случаями использования этой переменной в правиле. После унификации запроса с заголовком фразы интерпретатор переходит к обработке целей, содержащихся в теле этой фразы.
В данном случае Пролог не может найти в базе данных факта больше(слон, обезьяна) и переходит к рассмотрению второго правила. Оно гласит, что для того, чтобы получить ответ на вопрос больше_2(X,Y) (с фиксированными значениями переменных, то есть больше_2(слон, обезьяна)), Пролог должен ответить на два подвопроса больше(X, Z) и больше_2(Z, Y), опять же с соответствующими значениями переменных. Процесс просмотра базы знаний с самого начала повторяется до тех пор, пока факты, составляющие цепочку между слон и обезьяна, не будут найдены, а запрос успешно обработан.
Любая рекурсивная процедура должна включать по крайней мере по одной из ниже перечисленных компонент.
Нерекурсивную фразу, определяющую правило, применяемое в момент прекращения рекурсии.Рекурсивное правило, первая подцель которого вырабатывает новые значения аргументов, а вторая - рекурсивная подцель- использует эти значения.
Задание
Дана база данных "Родители", в которой предикат родитель(коля, андрей) означает, что Коля является родителем Андрея:
родитель(коля, андрей). родитель(андрей, саша). родитель(виктор, федор). родитель(виктор, петр). родитель(петр, елена).
Используя рекурсию, определите отношение предок/2 через отношение родитель/2. Будем говорить, что некоторый X является отдаленным предком некоторого Y, если между X и Y существует цепочка людей, связанных между собой отношением родитель - ребенок.
Решение логических задач
Интерпретатор Пролога можно заставить решать логические задачи, что недоступно большинству процедурных языков.
Многие логические задачи связаны с рассмотрением нескольких конечных множеств с одинаковым количеством элементов, между которыми устанавливается взаимно-однозначное соответствие. На языке Пролог эти множества можно описывать как базы данных, а зависимости между объектами устанавливать с помощью правил.
Пример
В автомобильных гонках три первых места заняли Алеша, Петя и Коля. Какое место занял каждый из них, если Петя занял не второе и не третье место, а Коля - не третье?
| Имя | I место | II место | III место |
| Алеша | |||
| Петя | - | - | |
| Коля | - |
Традиционным способом задача решается заполнением таблицы.По условию задачи Петя занял не второе и не третье место, а Коля - не третье. Это позволяет поставить символ '-' в соответствующих клетках. Между множеством имен участников гонки и множеством мест должно быть установлено взаимно-однозначное соответствие. Поэтому определяем занятое место сначала у Пети, затем у Коли и, наконец, у Алеши. В соответствующих клетках проставляем знак '+'. В каждой строке и каждом столбце должен быть только один такой знак.
| Имя | I место | II место | III место |
| Алеша | - | - | + |
| Петя | + | - | - |
| Коля | - | + | - |
Из последней таблицы следует, что Алеша занял третье место, Петя - первое, Коля - второе.
На языке Пролог структура программы будет следующей: сначала перечисляются данные - имена и номер занятого места, а затем записываются правила, связывающие эти два множества.
/* База данных имен */ имя(алеша). имя(петя). имя(коля).
/* База данных призовых мест */ место(первое). место(второе). место(третье).
/* Устанавливаем взаимно-однозначное соответствие между базами данных, X - элемент из базы данных имен, Y - элемент из базы данных занятых мест */
/* Петя занял не второе и не третье место */ соответствие(X, Y) :- имя(X), X=петя, место(Y), not(Y=второе), not(Y=третье).
/* Коля занял не третье место */ соответствие(X, Y) :- имя(X), X=коля, место(Y), not(Y=третье).
соответствие(X, Y) :- имя(X), X=алеша, место(Y).
/* У всех ребят разные места */ решение(X1,Y1,X2,Y2,X3,Y3) :- X1=петя, соответствие(X1,Y1), X2=коля, соответствие(X2,Y2), X3=алеша, соответствие(X3,Y3), Y1\=Y2, Y2\=Y3, Y1\=Y3.
Для получения ответа следует выполнить запрос
?- решение(X1,Y1,X2,Y2,X3,Y3).
В ответ Пролог выдаст имена ребят и занятые ими места. Проверьте, есть ли другие варианты ответов.
Пример
Витя, Юра и Миша сидели на скамейке. В каком порядке они сидели, если известно, что Миша сидел слева от Юры, а Витя слева от Миши.
В условии задачи перечисляются объекты одного типа, связанные между собой. Заполним базу данных:
/* Миша сидел слева от Юры */ слева(юра,миша).
/* Витя сидел слева от Миши */ слева(миша,витя).
Правило для установления следования объектов друг за другом будет таким:
/* Объекты X, Y и Z образуют ряд, если X слева от Y и Y слева от Z */
ряд(X, Y, Z) :- слева(Y, X), слева(Z, Y).
Количество аргументов в голове данного правила равно количеству объектов в задаче. Запрос ?- ряд(X, Y, Z). даст нам решение задачи.
Задание
Решите следующие логические задачи с помощью интерпретатора Пролога.
Трое ребят вышли гулять с собакой, кошкой и хомячком. Известно, что Петя не любит кошек и живет в одном подъезде с хозяйкой хомячка. Лена дружит с Таней, гуляющей с кошкой. Определить, с каким животным гулял каждый из детей.
Подсказка: прежде всего составьте таблицу, как в примере 1.
Витя, Юра и Миша сидели на скамейке. В каком порядке они сидели, если известно, что Юра сидел слева от Миши и справа от Вити.
Списки
Списки - одна из наиболее часто употребляемых структур в Прологе. При записи список заключают в квадратные скобки, а элементы списка разделяют запятыми, например,
[слон, лошадь, обезьяна, собака]
Это список из четырех атомов - слон, лошадь, обезьяна, собака.
Элементами списка могут быть любые термы Пролога, т. е. атомы, числа, переменные и составные термы, что позволяет, в частности, составлять списки из списков. Пустой список записывается как [ ].
[слон, [ ], X, предок(Х, том), [a,b,c], f(22)]
Первый элемент непустого списка называется головой, а остальная часть списка носит название хвост. У списка, состоящего только из одного элемента головой является этот единственный элемент, а хвостом - пустой список. Обозначение [H|T] используется для представления списка с головой H и хвостом T. Если символ | помещен перед последним термом списка, то это означает, что этот последний терм определяет другой список. Полный список получится, если соединить этот подсписок с последовательностью элементов, расположенных до черты.
В следующем примере 1 - голова списка, а [2, 3, 4, 5] - хвост. Пролог покажет это при помощи сопоставления списка чисел с образцом, состоящим из головы и хвоста.
?- [1, 2, 3, 4, 5] = [Head | Tail]. Head = 1 Tail = [2, 3, 4, 5] Yes
Здесь Head и Tail - только имена переменных. Мы могли бы использовать X и Y или какие-нибудь другие имена переменных с тем же успехом. Заметим, что хвост списка всегда является списком. Голова, в свою очередь, есть элемент списка, что верно и для всех других элементов, расположенных до вертикальной черты. Это позволяет получить, скажем, второй элемент списка.
Пример
Используем анонимные переменные для головы и списка, стоящего после черты, если нам нужен только второй элемент списка:
?- [слон, лошадь, осел, собака] = [_, X | _ ]. X = лошадь Yes
Рассмотрим несколько процедур обработки списков. Обратите внимание, что все они используют рекурсию, в которой терминальное (базовое) правило определено для пустого списка.
Пример
Напишем предикат для вычисления суммы всех элементов списка чисел.
сумма_списка([],0). сумма_списка([H|T],S):- number(H), сумма_списка(T,S1), S is S1+H.
Пример
Предикат место/ 3 успешен, если третий аргумент есть список, полученный вставкой первого аргумента в произвольное место списка, являющегося вторым аргументом.
место(E, L, [E|L]). место(E, [H|L], [H|Y]):- место(E, L,Y).
Посмотрим на результаты некоторых запросов, использующих этот предикат.
?- место(1,[2,3],X). X = [1, 2, 3] ; X = [2, 1, 3] ; X = [2, 3, 1] ; No
?- место(1,L,[2,1,3]). L = [2, 3] ; No
?- место(X,[2,3],[2,1,3]). X = 1 ; No
Пример
Предикат перестановка/2 выдает списки, полученные перестановкой элементов своего первого аргумента.
перестановка([],[]). перестановка([H|L],Z):- перестановка(L,Y), место(H,Y,Z).
Пример использования:
?- перестановка([a,b,c],X). X = [a, b, c] ; X = [b, a, c] ; X = [b, c, a] ; X = [a, c, b] ; X = [c, a, b] ; X = [c, b, a] ; No
И, наконец, приведем правило для печати всех возможных перестановок списка:
все_перестановки(L):- перестановка(L,R), write(R), nl, fail.
Первая подцель предиката вычисляет очередную перестановку, печатает ее и переходит к последней подцели - fail. Эта подцель всегда неуспешна, что заставляет Пролог вернуться к началу правила и продолжить поиск решения. Работа процедуры завершится, когда все перестановки будут исчерпаны:
?- все_перестановки(['маркиза', 'ваши прекрасные глаза', | 'сулят мне смерть от любви']).
[маркиза, ваши прекрасные глаза, сулят мне смерть от любви] [ваши прекрасные глаза, маркиза, сулят мне смерть от любви] [ваши прекрасные глаза, сулят мне смерть от любви, маркиза] [маркиза, сулят мне смерть от любви, ваши прекрасные глаза] [сулят мне смерть от любви, маркиза, ваши прекрасные глаза] [сулят мне смерть от любви, ваши прекрасные глаза, маркиза]
No
Пример
В старояпонском календаре был принят 60-летний цикл, состоящий из пяти 12-летних подциклов. Подциклы обозначались названиями цветов: зеленый, красный, желтый, белый и черный. Внутри каждого подцикла года носили названия животных: крыса, корова, тигр, заяц, дракон, змея, лошадь, овца, обезьяна, курица, собака и свинья.
Например, 1984 год - год начала очередного цикла - назывался Годом Зеленой Крысы.
Составим программу, которая по заданному номеру года нашей эры n печатает его название в старояпонском календаре. Рассмотрим два случая:
(1) значение n не меньше, чем 1984;
(2) значение n - любое натуральное число.
Воспользуемся встроенным предикатом nth0(индекс, список, элемент), который будет успешным, если элемент находится на месте с номером индекс, считая от 0. Для случая (1) используем предикат nam, для случая (2) предикат - nm.
color(N,X):- N1 is ((N-1984) mod 60)//12, nth0(N1, ['зеленый', 'красный', 'желтый', 'белый', 'черный'], X).
animal(N,X):- N1 is (N-1984) mod 12, nth0(N1, ['крыса', 'корова', 'тигр', 'заяц', 'дракон', 'змея', 'лошадь', 'овца', 'обезьяна', 'курица', 'собака', 'свинья'], X).
nam(N,[X,Y]):- number(N), color(N,X), animal(N,Y).
nm(N,X):- N>1983, nam(N,X). nm(N,X):- N<1984, N1 is N+60, nm(N1,X).
Задание
Напишите процедуры на языке Пролог для решения следующих задач и приведите примеры использования этих процедур.
Определите максимальный элемент списка чисел.Найдите второй по величине элемент списка.Сформируйте новый список из тех элементов данного списка, которые стоят на нечетных позициях. Например, из списка чисел [1, 2, 3, 4, 5, 6, 7] нужно получить следующий: [1, 3, 5, 7].
Термы и объекты
Программа на языке Пролог обычно описывает некую действительность. Объекты (элементы) описываемого мира представляются с помощью термов. Терм интуитивно означает объект. Существует 4 вида термов: атомы, числа, переменные и составные термы. Атомы и числа иногда группируют вместе и называют простейшими термами.
Атом - это отдельный объект, считающийся элементарным. В Прологе атом представляется последовательностью букв нижнего и верхнего регистра, цифр и символа подчеркивания '_', начинающейся со строчной буквы. Кроме того, любой набор допустимых символов, заключенный в апострофы, также является атомом. Наконец, комбинации специальных символов + - * = < > : & также являются атомами (следует отметить, что набор этих символов может отличаться в различных версиях Пролога).
Пример
Представленные далее последовательности являются корректными атомами:
b, abcXYZ, x_123, efg_hij, коля, слесарь, 'Это также атом Пролога', +, ::, <---->, ***
Числа в Прологе бывают целыми (Integer) и вещественными (Float).
Синтаксис целых чисел прост, как это видно из следующих примеров: 1, 1313, 0, -97. Не все целые числа могут быть представлены в машине, их диапазон ограничен интервалом между некоторыми минимальным и максимальным значениями, определенными конкретной реализацией Пролога. SWI-Prolog допускает использование целых чисел в диапазоне от -2147483648 (-231) до 2147483647 (231-1).
Синтаксис вещественных чисел также зависит от конкретной реализации. Мы будем придерживаться простых правил, понятных из следующих примеров: 3.14, -0.0035, 100.2. При обычном программировании на Прологе вещественные числа используются редко. Причина этого кроется в том, что Пролог - язык, предназначенный в первую очередь для обработки символьной, а не числовой информации. При символьной обработке часто используются целые числа, нужда же в вещественных числах невелика. Везде, где можно, Пролог старается привести число к целому виду.
Переменными в Прологе являются строки символов, цифр и символа подчеркивания, начинающиеся с заглавной буквы или символа подчеркивания:
X, _4711, X_1_2, Результат, _x23, Объект2, _
Последний пример ( единственный символ подчеркивания) является особым случаем - анонимной переменной (переменной без имени). Анонимная переменная применяется, когда ее значение не используется в программе. Возможное неоднократное употребление безымянной переменной в одном выражении применяется для того, чтобы подчеркнуть наличие переменных при отсутствии их специфической значимости.
Составные термы (функции) состоят из имени функции (нечислового атома) и списка аргументов (термов Пролога, то есть атомов, чисел, переменных или других составных термов), заключенных в круглые скобки и разделенных запятыми. Группы составных термов используют для составления фраз Пролога. Нельзя помещать символ пробела между функтором (именем функции) и открывающей круглой скобкой. В других позициях, однако, пробелы могут быть полезны для создания более читаемых программ. Ниже приведены два составных терма:
итого(клиент(X,23,_), 71) 'Что случилось?'(ничего)
При задании имен термов предпочтительнее использовать мнемонические ("говорящие") имена, так как терм a(ж), например, гораздо менее информативен, чем терм aвтор(жюль_верн).
Еще одной важной структурой данных в Прологе является список. Мы познакомимся с ним позднее. Сейчас отметим только один из видов списков - список символов. Такие списки могут быть представлены в виде строк, например, первый аргумент составного терма возраст("Борис",10) - строка. При записи строки заключаются в кавычки.
Унификация
Унификация есть основной механизм обработки запросов в логическом программировании. После того как пользователь посылает запрос интерпретатору, этот запрос активизируется. Интерпретатор приступает к анализу фраз базы данных в поисках первой фразы, заголовок которой будет унифицироваться с запросом. Для того чтобы запрос унифицировался с заголовком фразы, необходимо совпадение у них имени предиката, количества аргументов и унификация каждого из них.
Унификация термов, которыми являются аргументы, описывается приводимыми ниже правилами. В примерах используется предикат =, который пытается унифицировать свои аргументы.
Переменная унифицируется с атомом или составным термом. В результате этого переменная становится конкретизированной, т. е. принимает значение данного атома или терма. ?- X=коля. X=коля YesПеременная унифицируется с переменной, при этом они обе становятся как бы одной и той же переменной. ?- X=Y. X = _G161 Y = _G161 YesАнонимная переменная унифицируется с любым термом. ?- автор(пушкин)=_. YesАтом унифицируется с атомом, если они идентичны. ?- коля=коля. YesСоставной терм унифицируется с другим составным термом, если их имена и количество аргументов совпадает, а аргументы поддаются унификации. ?- отец(борис)=отец(X). X = борис Yes ?- дедушка(борис, Y)=отец(X). No
Пример
Термы больше(Х, собака) и больше(осел, собака) унифицируются, потому что переменная X может быть конкретизирована атомом осел:
?- больше(Х,собака) = больше(осел,собака). X = осел Yes
Рассматриваемый в следующем примере запрос не будет успешным, потому что переменная X не может быть конкретизирована двумя значениями 1 и 2 одновременно.
?- p(X,2,2) = p(1,Y,X). No
Если в этом примере вместо X мы используем анонимную переменную _, то унификация будет возможна, потому что при каждом использовании _ создается новая переменная. Смысл анонимности в том, что мы предоставляем Прологу возможность генерации имени для данной переменной и нам не нужны ни ее имя, ни ее значение. Переменная Y во время унификации конкретизируется значением 2:
?- p(_,2,2) = p(1,Y,_). Y = 2 Yes
Пример
В следующем запросе унификация возможна, хотя и нет специфических переменных, которые могли бы быть связаны или унифицированы (как в предыдущих примерах):
?- f(a,g(X,Y)) = f(X,Z), Z = g(W,h(x)). X = a Y = h(x) Z = g(a, h(x)) W = a Yes
Запросы к базе данных
Запрос - это последовательность предикатов, разделенных запятыми и завершающаяся точкой. На естественном языке запятая соответствует союзу "и", а на языке математической логики обозначает конъюнкцию. С помощью запросов можно "спрашивать" базу данных о том, какие утверждения являются истинными. Предикат запроса называется целью.
Простые вопросы, не содержащие никаких переменных, называют да-нет-вопросами. Они допускают лишь два возможных ответа: "Yes" означает наличие соответствующего факта в базе данных (первый запрос примера, приведенного ниже), "No" - его отсутствие (второй запрос). В случае ответа "Yes" говорят, что запрос завершился успехом, цель достигнута.
Пример
?- больше(слон, лошадь), больше(лошадь,осел). Yes
?- больше(слон, собака). No
Использование переменных в запросах позволяет задавать более сложные вопросы. Предположим, например, что мы хотим определить, какие животные больше осла? В следующем запросе переменная X обозначает искомый ответ:
?- больше(X, осел). X = лошадь Yes
При обработке запроса переменная X приняла значение "лошадь". Просматривая базу данных, интерпретатор обнаружил факт, утверждающий, что лошадь больше осла, и запрос был успешно выполнен.
Запросы с переменными могут иметь более одного решения. Первым всегда выводится то из решений, которое находится ближе к началу базы данных. Если нам достаточно только одного ответа, то можно нажать Enter и закончить поиск. В случае, если мы захотим получить очередной ответ, нужно нажать клавишу ; (точка с запятой), и Пролог начнет поиск других вариантов ответа на запрос. Сообщение "No" говорит об отсутствии очередного решения.
Пример
?- больше(осел, Х). X = собака; X = обезьяна; No
?- больше(X,Y). X = слон Y = лошадь;
X = лошадь Y = осел;
X = осел Y = собака;
X = осел Y = обезьяна; No
Задания
Загрузите в Пролог базу данных "Цвет" (файл task1.pl) и сформулируйте к ней следующие запросы. Машина красного цвета?Светофор желтого цвета?Море синего цвета и солнце желтого цвета?Добавьте в базу данных факт
цвет(трава, зеленый).
Сформулируйте запросы к измененной базе данных.
Какого цвета машина?Что в этой базе данных зеленого цвета?Какие элементы составляют эту базу данных и каковы соответствующие им цвета?
Аргументы командной строки
Как и другие языки программирования, Ruby позволяет передавать данные в программу, использую аргументы командной строки. Все, что при старте программы указывается после ее имени, интерпретатор помещает в специальный массив ARGV, работа с элементами которого нечем не отличается от работы с другими массивами. Можно, например, проверить, с правильным ли количеством аргументов командной строки была вызвана программа. Далее приводится программа, прерывающий свое выполнение, если число аргументов меньше 2:
=begin Напишите программу подсчета суммы всех нечетных чисел, заключенных в интервале от K до L, где K и L - аргументы командной строки =end
if ARGV.length < 2 puts "Слишком мало входных данных" exit(1) end
s = 0 k = ARGV[0].to_i l = ARGV[1].to_i for i in k .. l s += i if i%2 != 0 end puts "Сумма нечетных чисел в интервале " + "от #{k} до #{l} равна #{s}"
Для экстренного прерывания процесса выполнения программы здесь использован встроенный метод exit.
Пример 1.10.
(html, txt)
Задача
Числами Фибоначчи называется последовательность целых чисел, задаваемая соотношениями: а0 = 0, a1 = 1, an = an-1+an-2. Напишите программу, получающую с качестве аргумента командной строки целое число n, и печатающую n-е число Фибоначчи.
Вариант 1 - рекурсивная функция
В следующей программе первый элемент массива ARGV преобразовывается в целое число и передается в качестве аргумента рекурсивной функции fib.
def fib(n) if n<2 n else fib(n-2)+fib(n-1) end end n = ARGV[0].to_i puts "#{n}-е число Фибоначчи равно #{fib(n)}"
Для вычисления с помощью этой программы, размещенной в файлe fib.rb, например, 30-го числа Фибоначчи достаточно выполнить команду
ruby fib.rb 30
Данная программа использует двойную рекурсию, поэтому процесс вычисления займет достаточно заметное время.
Пример 1.11.
(html, txt)
Вариант 2 - использование массива
В следующем варианте решения этой задачи каждое число Фибоначчи вычисляется лишь один раз и сразу заносится в массив.
Для определения очередного элемента массива достаточно сложить два предыдущих.
n =ARGV[0].to_i f= [0, 1] fib = case n when 0 f[0] when 1 f[1] else for i in 2 .. n f[i] = f[i-1] + f[i-2] end f[n] end
puts "#{n}-е число Фибоначчи равно #{fib}"
Пример 1.12.
(html, txt)
Однако и у этой программы есть существенный недостаток - она хранит все промежуточные результаты, в то время как каждое предыдущее значение используется лишь дважды. Изменим программу так, чтобы она использовала только три переменных: вычисляемое значение и два предшествующих ему:
n =ARGV[0].to_i if n > 1 prev, beforePrev = 1, 0 for i in 2 .. n fib = prev + beforePrev prev, beforePrev = fib, prev end else fib = n end puts "#{n}-е число Фибоначчи равно #{fib}"
Пример 1.13.
(html, txt)
Включите в рассмотренные программы операторы, информирующие о продолжительности вычислений, и сравните их эффективность. Для этого найдите с помощью первой из рассмотренных программ 30, 31 и 32 числа Фибоначчи. Пользуясь второй и, тем более, третьей вы сможете вычислить достаточно большое число Фибоначчи, например, для вычисления 60000-го числа Фибоначчи, содержащего 12539 цифр на компьютере с процессором Celeron-500, программе, размещающей промежуточные результаты в массиве, потребовалось около 19 секунд, в то время как последняя программа вычислила его за 2 секунды.
Числа
Знакомство с представителями различных классов начнем с чисел. Целые числа в Ruby являются экземплярами класса Integer, который объединяет два подкласса: Fixnum или Bignum. Объектами класса Fixnum являются те целые, чье двоичное представление способно разместится в машинном слове (31 бит на большинстве компьютеров). Если число выходит за границы указанного диапазона, то оно автоматически преобразуется в объект класса Bignum, чей диапазон изменения ограничивается только объемом доступной памяти. Если в результате работы с объектами класса Bignum итоговое значение попадает в диапазон, задаваемый классом Fixnum, то выдаваемый результат преобразуется в экземпляр класса Fixnum.
| 123456 | Fixnum |
| 123_456 | Fixnum (подчеркивание игнорируется) |
| -543 | отрицательное Fixnum |
| 123_456_789_123_456 | Bignum |
| 0xaabb | шестнадцатеричное |
| 0377 | восьмеричное |
| -0b1010 | двоичное (отрицательное) |
| 0b001_001 | двоичное |
При записи целых чисел сначала указывается его знак (знак + обычно опускается). Далее следует основание системы счисления, в которой задается число (если оно отлично от 10): 0 - для восьмеричной, 0x - для шестнадцатеричной, 0b - для двоичной. Затем идет последовательность цифр, выражающих число в данной системе счисления. При записи больших чисел можно использовать символ подчеркивания, который игнорируется при обработке. В таблице представлены целые числа и указана их принадлежность к тому или иному классу.
Дробные числа задаются в десятичной системе счисления, при этом для отделения дробной части используется символ . (точка). Такие числа являются экземплярами класса Float, например, 12.34. Для задания дробных чисел может быть применена и экспоненциальная форма записи: два различных представления -.1234е2 и 1234е-2 задают одно и тоже число 12.34.
Для вычисления арифметических выражений применяются следующие операторы: + (сложение), - (вычитание), * (умножение), / (деление), % (остаток от деления), ** (возведение в степень). Порядок вычисления определяется стандартными приоритетами операций, а для его изменения используются круглые скобки.
Заметим, что если все аргументы выражения целые числа, то и результат будет целым, если же хотя бы одно из чисел, входящих в выражение - дробное, то и результат будет экземпляром класса Float.
Пример
Создайте файл с именем object.rb, в который поместите следующий фрагмент. Выполните программу и объясните результат.
puts 5/8 # 0 puts 5.0/8 # 0.625 puts 2**1000 puts ((2*500+1)*(2**500-1))
Пример 1.2.
(html, txt)
Отметим еще несколько методов, используемых при работе с числами (т. е. представителями класса Numeric). Среди них: ceil (нахождение наименьшего целого не меньшего, чем данное), floor (наибольшее целое, не большее данного), round (округление до ближайшего целого), получение абсолютной величины числа abs. Ниже приведены примеры использования этих методов.
puts 12.34.ceil # 13 puts 12.34.floor # 12 puts -12.ceil # -12 puts -12.floor # -12 puts 12.34.round # 12 puts 12.54.round # 13 puts -34.56.abs # 34.56
В Ruby имеется несколько методов, позволяющих преобразовывать объекты одного класса в другой.
| to_f | Преобразовать объект в экземпляр класса Float | 1234.to_f | 1234.0 |
| to_i | Преобразовать объект в экземпляр класса Fixnum или Bignum | -12.34.to_i | -12 |
Циклы
Для задания повторяющихся действий в большинстве языков программирования используются операторы цикла. В Ruby имеется два таких оператора - while и until, а также большое количество итераторов.
Оператор while выполняет операторы, составляющее его тело, ноль или более раз, до тех пор, пока истинно его условие, задаваемое некоторым логическим выражением. Его общий вид таков:
while <выражение> [do] ... тело цикла ... end
Другим оператором цикла является until, выполняющийся до тех пор, пока его условие ложно:
until <выражение> [do] ... тело цикла ... end
Пример Рассмотрим программу, печатающую числа от 1 до 5. Сначала используем оператор while, затем until. Обратите внимание, что условие окончания одного оператора цикла является отрицанием условия другого оператора.
i=1 while i <= 5 puts i; i += 1 end
# еще раз i=1 until i > 5 puts i; i += 1 end
Кроме этих двух операторов цикла в Ruby имеется большое число, так называемых, итераторов (iterate - повторять). Давайте посмотрим на примеры их использования. Конструкция
3.times do print "Ау! " end
использует итератор times. Цикл, заданный таким образом, выполнится ровно три раза.
В случае, когда нужно выполнить некоторые действия, зависящие от изменяемой величины, несколько раз, можно использовать итератор upto, так в процессе выполнения программы
0.upto(9) do |x| print x, " " end
будет напечатано 0 1 2 3 4 5 6 7 8 9.
Повтор от 0 до 12 с шагом 3 можно записать при помощи итератора step:
0.step(12, 3) {|x| print x, " " } # 0 3 6 9 12
При работе с массивами удобно использовать итератор each:
[1, 1, 2, 3].each {|k| print k, " " } # 1 1 2 3
Итератор for in очень похож на each, например, вывод, полученный в результате выполнения следующих двух конструкций одинаков.
for i in ["one", "two", "three"] print i, " " end
# то же самое ["one", "two", "three"].each{ |i| print i, " "}
Итератор for обычно используют там же, где и итератор each - при работе с массивами и диапазонами.
Общий вид оператора for таков:
for <переменная> in <выражение> [do] тело_итератора end
Пример
Перепишем программу печати чисел от 1 до 5 с использованием оператора for:
for i in 1 .. 5 puts i end
В этом примере мы снова воспользовались оператором задания диапазона .. (двоеточие), который позволил нам создать список чисел от 1 до 5 (включительно). Похожий оператор ... (троеточие) при создании диапазона не включает в него правый операнд. Фрагмент программы, расположенный ниже, эквивалентен предыдущему.
for i in 1 ... 6 puts i end
Пример
Рассмотрим несколько вариантов программы, вычисляющей факториал введенного числа.
Использование оператора while print "Введите целое положительное число: " str = gets.chop! # ввели строку num = str.to_i # преобразовали в число if num > 0 i = 1 fact = 1 while i <= num fact *= i i += 1 end puts "Факториал числа #{num} равен #{fact}" else puts "Вы ввели неположительное число" endИспользование оператора for print "Введите целое положительное число: " num = gets.to_i # строку сразу преобразовали в число if num > 0 fact = 1 for i in 1 .. num fact *= i end puts "Факториал числа #{num} равен #{fact}" else puts "Вы ввели неположительное число" endИспользование функции для определения факториала def fact(n) f = 1 1.step(n,1) {|k| f *= k} return f end print "Введите целое положительное число: " if (num = gets.to_i) > 0 print "#{num}! = #{fact(num)}\n" else puts "Факториал числа #{num} не определен\n" end
В последнем примере мы оформили вычисление факториала в виде функции и использовали итератор step, который обеспечил изменение переменной k с шагом 1.
Пример
Приведенная ниже программа запрашивает целое положительное число и определяет количество цифр в нем (обратите внимание на множественное присваивание).
print "Введите целое положительное число: " a, k = gets.to_i, 0 while a>0 a /= 10; k += 1 # отбросили последнюю цифру end print "Количество цифр в введенном числе равно #{k}.\n"
Пример
Пусть нужно ввести с клавиатуры массив чисел и напечатать сумму всех элементов. Приведем несколько решений этой задачи.
Сначала введем количество элементов массива, а затем заполним его элементами, одним за другим. Обратите внимание, что первый элемент массива имеет индекс 0, а последний - на единицу меньший, чем размерность массива. print "Введите число элементов массива: " sn = gets.chop!; n = sn.to_i b = Array.new(n) # создали массив из n элементов s = 0 # обнулили сумму for i in 0 .. n - 1 print "Введите #{i+1}-й элемент массива: " b[i] = gets.chop!.to_f; s = s + b[i] end print "Сумма всех элементов массива равна ", s, "\n"В этой версии программы все числа вводятся сразу в виде одной строки, в которой числа отделяется друг от друга пробелом (например, 23 -34.67 100.5).
Встроенный метод split разделяет строку на элементы массива, аргументом этого метода является разделитель (если разделителем является пробел, то можно вызвать этот метод без аргумента). Таким образом, если бы мы договорились разделять числа, например, точкой с запятой, то вызов метода выглядел бы так: a.split(';').
Для определения длины массива мы применили метод length (можно заменить на эквивалентный ему метод size).
puts "Введите массив чисел (разделяя их пробелами):" a = gets.chop! b = a.split # разбили строку на отдельные числа s = 0 for i in 0 .. b.length - 1 s += b[i].to_f end puts "Сумма всех элементов массива равна #{s}"
В Ruby имеются четыре конструкции, задаваемые ключевыми словами break, redo, next и retry, которые изменяют обычный порядок выполнения циклов. Их действие описано в следующей таблице.
| break | Немедленно прекращает выполнение цикла; управление передается на утверждение, расположенное сразу за циклом |
| redo | Повторяет тело цикла с начала, не пересчитывая условие выполнения цикла (не переходя к следующему элементу в случае итератора) |
| next | Пропускает часть тела цикла, следующую за ним, и переходит к следующей итерации |
| retry | Начинает выполнение цикла с самого начала |
Рассмотрим на примере итератора for действие указанных конструкций.
| for i in 1 .. 5 print i break if i == 3 print "*" end | Результат: 1*2*3 |
| for i in 1 .. 5 print i redo if i == 3 print "*" end | Результат:1*2*33333 ... выполнение цикла не прекращается |
| for i in 1 .. 5 print i next if i == 3 print "*" end | Результат: 1*2*34*5* |
| for i in 1 .. 5 print i retry if i == 3 print "*" end | Результат: 1*2*31*2*31*2*... выполнение цикла не прекращается |
Следующая программа начинает повторение цикла сначала, если при вводе указать символ y.
for i in 1 .. 5 print "Now at #{i}. Restart?(y/n) " retry if gets.chop == "y" end
Вот один из возможных вариантов выполнения этой программы:
Now at 1. Restart?(y/n) n Now at 2. Restart?(y/n) y Now at 1. Restart?(y/n) n ...
Пример 1.8.
(html, txt)
Задания
Напишите программу, вычисляющую сумму всех четных натуральных чисел, не превосходящих 1000.Напишите программу, определяющую максимальный элемент массива чисел.
def fact(n) f = 1 1.step(n,1) {|k| f *= k} return f end print "Введите целое положительное число: " if (num = gets.to_i) > 0 print "#{num}! = #{fact(num)}\n" else puts "Факториал числа #{num} не определен\n" end
puts print "Введите целое положительное число: " a, k = gets.to_i, 0 while a>0 a /= 10; k += 1 # отбросили последнюю цифру end print "Количество цифр в введенном числе равно #{k}.\n" puts
print "Введите число элементов массива: " sn = gets.chop!; n = sn.to_i b = Array.new(n) # создали массив из n элементов s = 0 # обнулили сумму for i in 0 .. n - 1 print "Введите #{i+1}-й элемент массива: " b[i] = gets.chop!.to_f; s = s + b[i] end print "Сумма всех элементов массива равна ", s, "\n" puts
puts "Введите массив чисел (разделяя их пробелами):"
a = gets.chop! b = a.split # разбили строку на отдельные числа s = 0 for i in 0 .. b.length - 1 s += b[i].to_f end puts "Сумма всех элементов массива равна #{s}" puts
=begin
for i in 1 .. 5 print i break if i == 3 print "*" end puts
for i in 1 .. 5 print i redo if i == 3 print "*" end puts
for i in 1 .. 5 print i next if i == 3 print "*" end puts
for i in 1 .. 5 print i retry if i == 3 print "*" end puts
=end
for i in 1 .. 5 print "Now at #{i}. Restart?(y/n) " retry if gets.chop == "y" end puts
Пример 1.8.
Задания
Напишите программу, вычисляющую сумму всех четных натуральных чисел, не превосходящих 1000.Напишите программу, определяющую максимальный элемент массива чисел.
type puts 0xaabb puts
| #!/usr/bin/env ruby puts 5/8 # 0 puts 5.0/8 # 0.625 puts 2**1000 puts ((2*500+1)*(2**500-1)) =begin puts (2**30-1).type a=0b001_001 puts a puts a.type a=12.34 puts a puts a.type a=12.34e2 puts a puts a.type =end puts 12.34.ceil # 13 puts 12.34.floor # 12 puts -12.ceil # -12 puts -12.floor # -12 puts 12.34.round # 12 puts 12.54.round # 13 puts -34.56.abs # 34.56 puts -12.34.to_i # -12 puts 1234.to_f # 1234.0 =begin puts 123_456_789. type puts 0xaabb puts -0b1010/0b10 puts 2/3.to_f =end |
| Пример 1.2. |
| Закрыть окно |
| #!/usr/bin/env ruby puts 'hello' # hello puts %q/hello/ # hello puts %q(hello) # hello puts 'hell\\o' # hell\o puts %q(hell\\o) # hell\o puts 'hell\'o' # hell'o puts %q(hell\'o) # hell\'o puts 'hel"l"o' # hel"l"o puts "hello" puts %Q/hello/ puts %Q!hello! puts %Q{hello} puts %Q(hello) puts %Q!hello! puts %<hello> puts %!hello! puts %*hello* puts %+hello+ puts %(hello) puts "Say \"Hello\"" # Say "Hello" puts "Say 'Hello'" # Say 'Hello' puts "a \t b" puts 'a \t b' puts "выражение 3*5+8 равно #{3*5+8}" puts 'выражение 3*5+8 равно #{3*5+8}' puts "работа с целыми числами: 5/8 = #{5/8}" puts "перевод в класс Float: 5/8 = #{5/8.to_f}" puts "-12.34".to_i puts "12.34".to_f puts "+12:34".to_i puts "12qq34".to_f puts 209.chr puts "123456789".reverse puts " 123 " puts " 123 ".strip puts "---22--23****".squeeze('*-') puts "---22--23****".squeeze puts "Дашка любит молоко, а Танька - квас".tr('ДТ','МД') puts "22+33=55".tr('25','47') puts "abcdef"[0].chr puts "abcdef".chop puts "abcdef".chop.chop puts "abcdef".delete("ea") puts "abcdef".delete('a-c') puts "abcdefabcdef".length puts "12345678".size puts "ABCDEF".downcase puts "abcdef".index("cd") puts "abcdefabcdef".index("cd",3) a="12345" puts "12345"[3].chr puts "12345"[0..3] puts "12345"[0,3] puts "привет".capitalize # Не работает с русскими буквами! puts "abcdabcd".index("cd",3) puts "*"+"123".ljust(9)+*" puts "*"+"123".center(9)+"*" puts "*"+"123".rjust(9)+"*" puts (eval "2**10") puts (eval ""мол".size * "око".size') =begin s="2*3+4" puts s puts "#{s}" puts eval(s) puts eval s puts s.eval # Ошибка! Неправильный вызов метода print "Введите команды:" eval gets.chop! =end |
| Пример 1.3. |
| Закрыть окно |
| #!/usr/bin/env ruby puts Time.now puts Time.now+60 # добавили 60 секунд к текущему времени puts Time.now-60 # отняли 60 секунд от текущего времени puts "До Нового года осталось #{365-Time.now.yday} дней" puts Time.now puts "Подождем 10 секунд." sleep(10) puts Time.now |
| Пример 1.4. |
| Закрыть окно |
| #!/usr/bin/env ruby puts "puts всегда завершается переходом к новой строке." print " А оператор print не делает этого по умолчанию, " print "как вы видите в этом примере.\n" print "print может быть вызван сразу ", "с несколькими аргументами.\n" p Time.now, Time.now+3600 printf "%8s~~%-8s\n", "abcd", "abcd" printf "%8-s::%8s\n", "abcd", "abcd" printf "%06d\n", 2**10; printf "%+6d\n", 2**10 printf "%6d\n", 2**10; printf "%+6d\n", 2.5*1.3 printf "%4.3f\n", 2.5*1.3 printf "-2/7=%+1.6f, -2/6=%2.15f\n", -2/7.to_f, -2/6.to_f puts "*\t*\t*\t*\t*" puts " 1234567 1234567 1234567 1234567 " |
| Пример 1.5. |
| Закрыть окно |
| #!/usr/bin/env ruby number = 342 puts " Исходное число равно #{number}" n1 = number/100 # число сотен n2 = (number/10)%10 # число десятков n3 = number%10 # число единиц answer = n1*100 + n3*10 + n2 puts "Результат #{answer}" |
| Пример 1.6. |
| Закрыть окно |
| #!/usr/bin/ env ruby if 23 puts "23 есть ИСТИНА" end if "qq" puts "И любая строка есть ИСТИНА" end puts # Определение метода оценки величины выражения def howBigPrint(i) if i < 10 puts "Число #{i} меньше 10" elsif i < 20 puts "Число #{i} между 10 и 20" elsif i < 30 puts "Число #{i} между 20 и 30" else puts "Число #{i} больше или равно 30" end end # Использование метода ... howBigPrint(7); howBigPrint(15) howBigPrint(23); howBigPrint(105) puts # Метод оценки величины выражения # теперь возвращает строку def howBig(i) if i < 10 then "Аргумент меньше 10" elsif i < 20 then "Аргумент между 10 и 20" elsif i < 30 then "Аргумент между 20 и 30" else "Аргумент больше или равно 30" end end # Использование метода ... puts howBig(7); puts howBig(15) puts howBig(23); puts howBig(105) puts i = 23 i < 100 ? puts("Мало") : puts("Значительно больше") i = 1234 s = i < 100 ? "Мало" : "Значительно больше" puts s puts "Перевертыш" puts "Введите фразу:" a = gets.chop!.delete(' ') # удалили все пробелы a = a.tr('A-Z,А-Я', 'a-z,а-я') # замена букв на прописные str = "палиндром" str = "не " + str if a != a.reverse # проверка puts "Введенная фраза - " + str + "." print "Введите неотрицательное целое число: " i= gets.to_i s = case i when 0 .. 9 "однозначное" when 10 .. 99 "двузначное" when 100 .. 999 "трехзначное" else "огромное" end puts "Введено #{s} число." |
| Пример 1.7. |
| Закрыть окно |
| #!/usr/bin/env ruby i=1 while i <= 5 puts i; i += 1 end puts # еще раз i=1 until i > 5 puts i; i += 1 end puts 3.times do print "Ау! " end puts 0.upto(9) do |x| print x, " " end puts 0.step(12, 3) {|x| print x, " " } # 0 3 6 9 12 puts [1, 1, 2, 3].each {|k| print k, " " } # 1 1 2 3 puts for i in ["one", "two", "three"] print i, " " end puts # то же самое ["one", "two", "three"].each{ |i| print i, " "} puts for i in 1..5 puts i end puts for i in 1 ... 6 puts i end puts print "Введите целое положительное число: " str = gets.chop! # ввели строку num = str.to_i # преобразовали в число if num > 0 i = 1 fact = 1 while i <= num fact *= i i += 1 end puts "Факториал числа #{num} равен #{fact}" else puts " Вы ввели неположительное число" end puts print "Введите целое положительное число: " num = gets.to_i # строку сразу преобразовали в число if num > 0 fact = 1 for i in 1 .. num fact *= i end puts "Факториал числа #{num} равен #{fact}" else puts "Вы ввели неположительное число" end puts def fact(n) f = 1 1.step(n,1) {|k| f *= k} return f end print "Введите целое положительное число: " if (num = gets.to_i) > 0 print "#{num}! = #{fact(num)}\n" else puts "Факториал числа #{num} не определен\n" end puts print "Введите целое положительное число: " a, k = gets.to_i, 0 while a>0 a /= 10; k += 1 # отбросили последнюю цифру end print "Количество цифр в введенном числе равно #{k}.\n" puts print "Введите число элементов массива: " sn = gets.chop!; n = sn.to_i b = Array.new(n) # создали массив из n элементов s = 0 # обнулили сумму for i in 0 .. n - 1 print "Введите #{i+1}-й элемент массива: " b[i] = gets.chop!.to_f; s = s + b[i] end print "Сумма всех элементов массива равна ", s, "\n" puts puts "Введите массив чисел (разделяя их пробелами):" a = gets.chop! b = a.split # разбили строку на отдельные числа s = 0 for i in 0 .. b.length - 1 s += b[i].to_f end puts "Сумма всех элементов массива равна #{s}" puts =begin for i in 1 .. 5 print i break if i == 3 print "*" end puts for i in 1 .. 5 print i redo if i == 3 print "*" end puts for i in 1 .. 5 print i next if i == 3 print "*" end puts for i in 1 .. 5 print i retry if i == 3 print "*" end puts =end for i in 1 .. 5 print "Now at #{i}. Restart?(y/n) " retry if gets.chop == "y" end puts |
| Пример 1.8. |
| Закрыть окно |
| #!/usr/bin/env ruby # 1 print " Введите первое число: "; a = gets.to_i print "Введите второе число: "; b = gets.to_i k = a >= b ? a : b # теперь k - максимум until (a%k == 0)&& (b%k == 0) k-=1 end print "НОД(#{a},#{b}) = #{k}\n" #2 Алгоритм Евклида print "Введите первое число: "; a = gets.to_i print "Введите второе число: "; b = gets.to_i m, n = a, b while !((m == 0) || (n == 0)) if m >= n m = m - n else n = n - m end end k = m == 0 ? n : m print "НОД(#{a},#{b}) = #{k}\n" |
| Пример 1.9. |
| Закрыть окно |
| #!/usr/bin/env ruby = begin Напишите программу подсчета суммы всех нечетных чисел, заключенных в интервале от K до L, где K и L - аргументы командной строки =end if ARGV.length < 2 puts "Слишком мало входных данных" exit(1) end s = 0 k = ARGV[0].to_i l = ARGV[1].to_i for i in k .. l s += i if i%2 != 0 end puts "Сумма нечетных чисел в интервале " + "от #{k} до #{l} равна #{s}" |
| Пример 1.10. |
| Закрыть окно |
| #!/usr/bin/env ruby =begin Напишите программу, получающую с качестве аргумента командной строки целое число n, и печатающую n-е число Фибоначчи. =end def fib(n) if n<2 n else fib(n-2)+fib(n-1) end end t1 = Time.now n = ARGV[0].to_i puts "#{n}-е число Фибоначчи равно #{fib(n)}" t2 = Time.now puts "Время расчета около #{(t2-t1).round} сек." |
| Пример 1.11. |
| Закрыть окно |
| #!/usr/bin/env ruby =begin Напишите программу, получающую с качестве аргумента командной строки целое число n, и печатающую n-е число Фибоначчи. =end t1 = Time.now n =ARGV[0].to_i f= [0, 1] fib = case n when 0 f[0] when 1 f[1] else for i in 2 .. n f[i] = f[i-1] + f[i-2] end f[n] end puts "#{n}-е число Фибоначчи равно #{fib}" t2 = Time.now puts "Время расчета около #{(t2-t1).round} сек." a = fib.to_s.split('") puts "Количество цифр в #{n}-м числе Фибоначчи равно #{a.size}." |
| Пример 1.12. |
| Закрыть окно |
| #!/usr/bin/env ruby =begin Напишите программу, получающую с качестве аргумента командной строки целое число n, и печатающую n-е число Фибоначчи. =end t1 = Time.now n =ARGV[0].to_i if n > 1 prev, beforePrev = 1, 0 for i in 2 .. n fib = prev + beforePrev prev, beforePrev = fib, prev end else fib = n end puts "#{n}-е число Фибоначчи равно #{fib}" t2 = Time.now puts "Время расчета около #{(t2-t1).round} сек." a = fib.to_s.split("') puts "Количество цифр в #{n}-м числе Фибоначчи равно #{a.size}." |
| Пример 1.13. |
| Закрыть окно |
| #!/usr/bin/env ruby # 1 f = File.new("fio.txt") n = 1 student = f.readlines student.each{ |i| print n, ". ", i n += 1 } puts # 2 f = File.new("fio.txt") n = 1 student = f.readlines student.each{ |i| i.chop! fio = i. split print n, ". ", fio[0], " ", fio[0][0].chr, ". ", fio[1][0].chr, ".\n" n += 1 } |
| Пример 1.14. |
| Закрыть окно |
| #!/usr/bin/env ruby # Метод Монте-Карло puts "Введите количество точек:" n1, n, t1 = 0, eval(gets.chop), Time.now for i in 1 .. n x = 2*rand() - 1 y = 2*rand() - 1 # проверяем попадание внутрь круга n1 += 1 if (x**2 + y**2) < 1 end puts "PI=#{4.0*n1/n}" t2 = Time.now puts "Число точек #{n}, время расчета " + "около #{(t2 - t1).round} сек." |
| Пример 1.15. |
| Закрыть окно |
| #!/usr/bin/env ruby class Car @@NUM_CARS = 0 def initialize @@NUM_CARS = @@NUM_CARS + 1 puts @@ NUM_CARS end end class SportsCar < Car end class FamilyCar < Car end a = Car.new b = SportsCar.new c = FamilyCar.new |
| Пример 1.16. |
| Закрыть окно |
Язык программирования Ruby
Ruby - один из самых молодых языков программирования. Своим именем он обязан драгоценному камню рубину (по аналогии с другим широко распространенным языком программирования Perl - жемчуг). Вот как описывает Ruby его создатель, японский программист Юкихиро Мацумото (Yukihiro Matsumoto): "Это мощный и динамический объектно-ориентированный язык с открытыми исходниками, который я начал разрабатывать в 1993 году. Ruby работает на многих платформах, включая Linux и многие реализации Unix, MS-DOS, Windows 9x/2000/NT, BeOS и MacOS. Главная цель Ruby - эффективность разработки программ, и пользователи найдут, что программирование на нем эффективно и даже забавно".
В Японии Ruby сильно потеснил такие известные языки как Python и Perl (а книга "Ruby the Object-Oriented Scripting Language" стала бестселлером) и начал распространяться по всему миру. За последний год появились три англоязычных книги, посвященные Ruby (к сожалению, пока не имеющие русского перевода). У этого языка очень неплохие шансы стать действительно популярным - ведь он вобрал в себя достоинства других языков, учтя их недостатки.
Ruby входит в стандартную поставку ОС Linux (начиная с версии 7.2), а пользователям MS Windows для первого знакомства стоит порекомендовать его несколько устаревшую версию (1,2 Мбайт), легко умещающуюся на одной дискете, которая включает, помимо интерпретатора языка и библиотек, руководство пользователя, FAQ (ответы на часто задаваемые вопросы) и множество примеров. Ruby является свободно распространяемым продуктом, поэтому вы можете не беспокоиться ни о его стоимости, ни об ограничениях в его использовании.
Этот язык несомненно является одним из лучших в качестве первого языка программирования, изучаемого студентами и школьниками. Быстрый цикл разработки (редактирование - запуск - редактирование), использование интерпретатора, изначальная объектно-ориентированность языка, нетипизированные переменные, которые не требуют объявления - все это позволяет учащимся сконцентрировать свое внимание на общих принципах программирования.
В дальнейшем изложении мы будем ориентироваться на работу в ОС Linux. Использование Ruby в других операционных системах практически ничем не отличается, а результаты выполнения не зависят от используемой ОС.
Сначала проверим, установлен ли интерпретатор Ruby в системе или нет. В окне shell введите команду ruby -v (этот ключ требует вывода версии языка). Если следующее сообщение появится, то Ruby установлен (версия, дата и платформа могут отличаться):
ruby 1.6.4 (2001-06-04) [i386-linux-gnu]
Файлы, содержащие программы на языке Ruby, обычно имеют расширение rb. По давней программистской традиции наша первая программа будет печатать фразу "Hello, World!". При помощи любого редактора plain-текста (emacs, kwrite, notebook и т. п.) создадим файл hello.rb, в который поместим текст
puts "Hello, World!"
Для выполнения этой программы в командной строке введите
ruby hello.rb
В результате выполнения программы в командном окне будет напечатана требуемая фраза.
Второй способ выполнения программ доступен пользователям не всех операционных систем, в которых функционирует Ruby. Пользователям ОС Linux следует поместить в начало файла с текстом программы следующую строку:
#!/usr/bin/env ruby
Она обязательно должна начинаться с первой позиции. Затем нужно изменить права доступа файла с программой, сделав его исполняемым: chmod +x hello.rb. Теперь для запуска программы достаточно ввести команду
./hello.rb
Для того чтобы сделать программу более понятной человеку, который ее читает, вставляются комментарии. Однострочные комментарии начинаются с символа # и продолжаются до конца строки. Многострочные комментарии заключают в специальные "скобки" - все, что располагается между строками =begin и =end, считается комментарием. Например,
#!/usr/bin/env ruby =begin Это комментарий =end puts "Hello, World!" # Это тоже комментарий
Программа на языке Ruby, часто называемая скриптом, есть последовательность инструкций (утверждений, предложений). Каждая инструкция по умолчанию заканчивается концом строки.
Если же по каким- либо причинам требуется разместить несколько инструкций на одной строке, то их нужно разделять символом ; (точка с запятой). С другой стороны, иногда инструкция не помещается на одной строке. В этом случае символ \ сигнализирует о том, что ее продолжение располагается в следующей строке.
Пример
#!/usr/bin/env ruby # Инструкция заканчивается концом строки puts "Hello, World!"
# Несколько инструкций в одной строке puts "Это тест, "; puts "демонстрирующий работу Ruby."
# Незаконченная инструкция, # продолжение которой на следующей строке puts "Программирование на Ruby - " + "приятное занятие."
# Утверждение, разделенное на несколько строк puts \ "И мы обязательно этому научимся!"
Инструкция (утверждение) чаще всего представляет собой некую последовательность операторов, применяемых к различным выражениям, и (возможно) вызовов функций.
Далее строка #!/usr/bin/env ruby в тексты программ не включается.
НОД и алгоритм Евклида
При рассмотрении задач, связанных с обработкой целых чисел, часто приходится сталкиваться с понятием НОД - наибольшего общего делителя чисел. Известно много алгоритмов вычисления НОД, мы рассмотрим лишь два из них.
Задача
Напишите программу, вычисляющую НОД(a,b) - наибольший общий делитель двух введенных с клавиатуры неотрицательных целых чисел a и b, не равных нулю одновременно.
Вариант 1
Определим максимум из этих чисел и, последовательно уменьшая его, будем искать число, на которое делятся и a и b. Программа обязательно завершит свою работу, так как в самом неудачном случае, когда эти числа взаимно просты, k станет равно 1, а на 1 делятся все числа, следовательно выполнение цикла прекратится.
print "Введите первое число: "; a = gets.to_i print "Введите второе число: "; b = gets.to_i
k = a >= b ? a : b # теперь k - максимум until (a % k == 0) and (b % k == 0) k -= 1 end print "НОД(#{a},#{b}) = #{k}\n"
Вариант 2 - алгоритм Евклида
Алгоритм Евклида основан на следующих свойствах НОД: для всех a и b, больших или равных 0, выполнены равенства
НОД(a, b) = НОД(a - b, b)= НОД(a, b - a); НОД(a, 0) = НОД(0, a) = a
Ниже приведен текст программы, реализующей алгоритм Евклида.
print "Введите первое число: "; a = gets.to_i print "Введите второе число: "; b = gets.to_i m, n = a, b while !((m == 0) || (n == 0)) if m >= n m = m - n else n = n - m end end
k = m == 0 ? n : m print "НОД(#{a},#{b}) = #{k}\n"
Пример 1.9.
(html, txt)
Объекты и методы
При описании Ruby было отмечено, что он является объектно-ориентированным языком программирования. Это означает что все, с чем работает программа, является объектом, при этом вычисление осуществляется посредством взаимодействия объектов. Каждый объект есть представитель (экземпляр) некоторого класса и его поведение (функциональность) определяется именно им. Тем самым все объекты, которые являются экземплярами одного класса, могут выполнять одни и те же действия, называемые методами. Для того чтобы применить метод к некоторому объекту используется оператор вызова метода, обозначаемый символом . (точка): после указания объекта ставится точка, а затем указывается применяемый метод.
Пока мы не будем вдаваться в особенности объектно-ориентированного программирования (тем более, что в различных языках программирования по разному трактуется концепция ООП), а лишь познакомимся с некоторыми "простейшими" объектами, без которых невозможно приступать к дальнейшему изучению языка. Это представители так называемых "встроенных" классов. Среди них:
true - логическая величина, означающая истину; единственный представитель класса TrueClass;
false - логическая величина, означающая ложь; единственный представитель класса FalseClass;
числа - представители класса Numeric, который в качестве подклассов содержит дробные (Float) и целые числа (Integer);
строки - представители класса String;
nil - "ничто"; единственный представитель класса NilClass.
моменты времени - представители класса Time.
Операторы ветвления
Условный оператор, называемый также оператором выбора, позволяет в зависимости от истинности или ложности некоторого условия выполнять ту или иную последовательность команд.
Ruby поддерживает все конструкции выбора, традиционно используемые в других языках программирования. Но прежде чем говорить о них, остановимся на некоторых особенностях Ruby при вычислении истинности отдельных выражений.
Следует запомнить, что только false и nil трактуются как ложные в логическом контексте. Все остальное, что вычисляется, является истинным. Для того чтобы лучше понять смысл данного высказывания, выполните следующую программу:
if 23 puts "23 есть ИСТИНА" end
if "qq" puts "И любая строка есть ИСТИНА" end
Ruby поддерживает все стандартные логические операторы, а также дополнительный оператор defined?. Для конъюнкции двух логических выражений используются and и &&. Их результат будет истинен только если инстинны оба операнда. Эти функции вычисляют второй операнд лишь тогда, когда первый истинен, а отличаются они только своим приоритетом (приоритет оператора and меньше &&).
В свою очередь результатом выполнения операторов or и ||(дизъюнкции) будет истина, если хотя бы один из операндов истинен. Они вычисляют второй оператор только в том случае, если первый окажется ложным. Как и в случае с оператором and, оператор or имеет меньший приоритет по сравнению с || (отметим, что оператор and имеет приоритет, равный приоритету оператора or, в то время как приоритет && выше, чем у ||).
Операторы not и ! возвращают значение, противоположное своему аргументу (если аргумент истинен, то результат ложен, и наоборот). Между собой отличаются только приоритетом.
Оператор defined? возвращает nil, если его аргумент не определен, и его описание в противном случае. Ниже приведены примеры применения этого оператора.
puts defined? 1 puts defined? dummy puts defined? printf puts defined? (c, d = 1, 2) puts defined? 42.abs
В логических выражениях допускаются также следующие операции сравнения: == <, <=, >=, > !=.
Синтаксис условного оператора if в языке Ruby аналогичен его синтаксису в большинстве других языков программирования.
# Определение метода оценки величины выражения def howBigPrint(i) if i < 10 puts "Число #{i} меньше 10" elsif i < 20 puts "Число #{i} между 10 и 20" elsif i < 30 puts "Число #{i} между 20 и 30" else puts "Число #{i} больше или равно 30" end end # Использование метода ... howBigPrint(7); howBigPrint(15) howBigPrint(23); howBigPrint(105)
Общая форма оператора if такова:
if <логическое_выражение> [then] тело_оператора elsif <логическое_выражение> [then] тело_оператора ... else тело_оператора end
Здесь <логическое_выражение>; может быть любым фрагментом кода на языке Ruby, результатом вычисления которого является логическая величина (с учетом сказанного выше). Слово then отделяет тело оператора от условия. Запись его в квадратных скобках означает, что оно может быть опущено, если тело начинается с новой строки. Значение, возвращаемое оператором if, есть результат последнего вычисленного выражения. Изменим наш пример, чтобы продемонстрировать сказанное:
# Метод оценки величины выражения # теперь возвращает строку def howBig(i) if i < 10 then "Аргумент меньше 10" elsif i < 20 then "Аргумент между 10 и 20" elsif i < 30 then "Аргумент между 20 и 30" else "Аргумент больше или равно 30" end end # Использование метода ... puts howBig(7); puts howBig(15) puts howBig(23); puts howBig(105)
Для выполнения одного варианта из двух возможных используется следующая форма оператора if:
if <логическое_выражение> [then] тело_оператора else тело_оператора end
В следующем фрагменте сравнивается значение переменной i с числом 100.
if i < 100 puts "Мало" else puts "Значительно больше" end
Оператор if может использоваться в правой части оператора присваивания, например,
str = if i < 100 then "Мало" else "Побольше" end puts str
Для аналогичных целей используется и тернарный оператор
логическое_выражение ? выражение1 : выражение2
Если логическое_выражение истинно, то выполняется выражение1, иначе - выражение2. Посмотрите на примеры использования этого оператора:
i = 23 i < 100 ? puts("Мало") : puts("Значительно больше") i = 1234 s = i < 100 ? "Мало" : "Значительно больше" puts s
Как видите, этот оператор особенно удобен, если требуется переменной присвоить одно из двух значений.
Пример
Напишите программу, определяющую четность введенного числа.
print "Введите целое число: " a = gets.to_i str = a%2 == 0 ? "четно" : "нечетно" puts "Число #{a} " + str
Если требуется выполнить последовательность операторов только в том случае, когда выполнено некоторое условие, то используется форма
if <логическое_выражение> [then] тело_оператора end
Для этих же целей можно использовать и модифицированный оператор if:
выражение if <логическое_выражение>
Ниже приводятся две версии фрагмента программы, использующей оператор if:
if radiation > 3000 puts "Радиационная опасность!" end # то же самое puts "Радиационная опасность!" if radiation > 3000
Пример
Напишите программу, определяющую, является ли введенная фраза палиндромом (перевертышем).
puts "Введите фразу:" a = gets.chop!.delete(' ') # удалили все пробелы a = a.tr('A-Z,А-Я', 'a-z,а-я') # замена букв на прописные str = "палиндром" str = "не " + str if a != a.reverse # проверка puts "Введенная фраза - " + str + "."
При выборе из большего числа альтернатив удобнее использовать оператор case. Ниже приведен его общий вид (части, заключенные в квадратные скобки, могут быть опущены).
case <выражение> when <тест1> [then] ... when <тест2> [then] ... when <тестN> [then] ... [else ... ] end
В операторе case <выражение> последовательно сравнивается с выражениями <тест> до тех пор пока, оно не совпадет с одним из них (сравнение производится при помощи операции ==), после чего выполняется соответствующий фрагмент кода.Оператор case возвращает значение последнего вычисленного выражения, или nil, если такого не было.
s = case i when 0 .. 9 "однозначное" when 10 .. 99 "двузначное" when 100 .. 999 "трехзначное" else "огромное" end puts "Введено #{s} число."
Здесь мы снова воспользовались оператором .. (двоеточие), который возвращает список целых чисел, заключенных между левым и правым операндами (включая их самих).
Пример 1.7.
(html, txt)
Задания
Напишите программу, печатающую максимальное и минимальное из трех введенных чисел.Напишите программу, печатающую название месяца по порядковому номеру.
Оператор case возвращает значение последнего вычисленного выражения, или nil, если такого не было.
s = case i when 0 .. 9 "однозначное" when 10 .. 99 "двузначное" when 100 .. 999 "трехзначное" else "огромное" end puts "Введено #{s} число."
Здесь мы снова воспользовались оператором .. (двоеточие), который возвращает список целых чисел, заключенных между левым и правым операндами (включая их самих).
#!/usr/bin/env ruby if 23 puts "23 есть ИСТИНА" end
if "qq" puts "И любая строка есть ИСТИНА" end puts
# Определение метода оценки величины выражения def howBigPrint(i) if i < 10 puts "Число #{i} меньше 10" elsif i < 20 puts "Число #{i} между 10 и 20" elsif i < 30 puts "Число #{i} между 20 и 30" else puts "Число #{i} больше или равно 30" end end # Использование метода ... howBigPrint(7); howBigPrint(15) howBigPrint(23); howBigPrint(105) puts
# Метод оценки величины выражения # теперь возвращает строку def howBig(i) if i < 10 then "Аргумент меньше 10" elsif i < 20 then "Аргумент между 10 и 20" elsif i < 30 then "Аргумент между 20 и 30" else "Аргумент больше или равно 30" end end # Использование метода ... puts howBig(7); puts howBig(15) puts howBig(23); puts howBig(105)
puts i = 23 i < 100 ? puts("Мало") : puts("Значительно больше") i = 1234 s = i < 100 ? "Мало" : "Значительно больше" puts s
puts "Перевертыш"
puts "Введите фразу:" a = gets.chop!.delete(' ') # удалили все пробелы a = a.tr('A-Z,А-Я', 'a-z,а-я') # замена букв на прописные str = "палиндром" str = "не " + str if a != a.reverse # проверка puts "Введенная фраза - " + str + "."
print "Введите неотрицательное целое число: " i= gets.to_i s = case i when 0 .. 9 "однозначное" when 10 .. 99 "двузначное" when 100 .. 999 "трехзначное" else "огромное" end puts "Введено #{s} число."
Пример 1.7.
Задания
Напишите программу, печатающую максимальное и минимальное из трех введенных чисел.Напишите программу, печатающую название месяца по порядковому номеру.
Переменные и константы
В этом курсе мы будем использовать так называемые локальные переменные. Имена локальных переменных начинаются со строчной латинской буквы (от a до z) или символа подчеркивания и продолжаются любой комбинацией латинских букв, цифр и символа подчеркивания. Те же правила распространяются и на имена методов.
В языке имеется небольшое множество зарезервированных слов, которые нельзя использовать в качестве имен переменных и методов.
| __FILE__ | and | def | end | in | or | self | unless |
| __LINE__ | begin | defined? | ensure | module | redo | super | until |
| BEGIN | break | do | false | next | rescue | then | when |
| END | case | else | for | nil | retry | true | while |
| alias | class | elsif | if | not | return | undef | yield |
Кроме локальных переменных Ruby поддерживает и другие их виды - глобальные переменные, переменные классов и экземпляров. Принадлежность к каждому из этих видов определяются символом, стоящим перед именем переменной (префиксом): символ $ задает глобальную переменную, @ - переменную экземпляра, @@ - переменную класса. Локальные переменные не имеют префикса. Имена констант и классов должны начинаться с прописной латинской буквы (A-Z) и, аналогично переменным, продолжаются любой комбинацией латинских букв, цифр и символа подчеркивания.
Локальная переменная создается динамически в момент, когда ей в процессе выполнения программы первый раз присваивается какое-то значение. Оператор присваивания имеет вид знака = (равно), например, a = 1; b = a; name = "Иван". Переменные могут использоваться во всех выражениях Ruby аналогично соответствующим объектам:
a = "Привет всем!" puts a
В Ruby переменные есть ссылки на объекты. Их следует трактовать как некие метки. Для того чтобы лучше понять эту концепцию проведем следующую аналогию: пусть у вас есть некоторая коробка (объект), вы берете наклейку (переменную), подписываете ее (даете имя переменной), после чего наклеиваете ее на коробку (объект). В Ruby переменные не имеют типа, так как они есть всего лишь ссылки на объекты произвольных типов.
Проиллюстрируем сказанное следующим примером:
a = "one" puts a puts a.type a = 23 puts a puts a.type
Обратите внимание на метод type, возвращающий тип объекта. При первом использовании переменная a есть ссылка на объект класса String, затем мы присваиваем этой переменной другое значение (наклеиваем ту же этикетку на новый объект), после чего она становится ссылкой на экземпляр класса Fixnum.
Ruby поддерживает также и присваивание с операцией. Результат выполнения следующих двух операторов одинаковы:
a+=12 a=a+12
Общая форма подобных операторов выглядит так:
выражение1 операция= выражение2
что соответствует оператору
выражение1 = выражение1 операция выражение2
Между знаком операции и символом равенства не должно быть пробела. Такой синтаксис допустим для следующих операций:
+, -, *, /, %, **, &, |, ^, <<, >>, &&, |
Когда требуется присвоить значение нескольким переменным, можно использовать множественное присваивание:
a, b, c = 1, 2, 3
Пример
Пусть требуется обменять значения двух переменных, не вводя вспомогательную переменную. С использованием множественного присваивания это можно записать так:
a, b = b, a
Данный пример объясняет, почему эту форму оператора присваивания называют также "параллельным присваиванием".
Мы уже упоминали одну из замечательных возможностей Ruby - подстановку. Она позволяет выполнять разнообразные трюки со строкой, заключенной в двойные кавычки, например,
magic = 42 puts "Секретное число равно #{magic - 3}!!"
Когда Ruby находит конструкцию #{выражение} внутри строки, заключенной в двойные кавычки, то заменяет эту ее часть на результат вычисления выражения.
Пример
Дано трехзначное число. Напечатать число, получающееся при перестановке цифр десятков и единиц заданного числа.
number = 342 puts "Исходное число равно #{number}" n1 = number/100 # число сотен n2 = (number/10)%10 # число десятков n3 = number%10 # число единиц answer = n1*100 + n3*10 + n2 puts "Результат #{answer}"
Пример 1.6.
(html, txt)
Иногда возникает необходимость указать, что тот или иной объект в программе является неизменяемым. Такие объекты называются константами. В Ruby имена констант, также как и имена классов, должны начинаться с заглавной буквы (есть определенная традиция задавать имена констант, состоящие из одних заглавных букв). Рассмотрим следующий фрагмент программы:
NUM = 234 p NUM # 234 NUM = "qq" # warning: already initialized constant NUM p NUM # "qq"
Как видим, интерпретатор выдал предупреждение о том, что константа NUM уже была определена ранее. Тем не менее значение константы было изменено.
Задания
Напишите программу, печатающую количество квадратов со стороной 130 мм, которое можно отрезать от прямоугольника со сторонами 543x130 мм.Напишите программу, которая по данному числу a, не используя никаких арифметических операций, кроме умножения, получает a8 за три операции.
Работа с файлами
Ввод данных с клавиатуры в процессе выполнения программы удобен только в случае небольших объемов. В других ситуациях необходимо чтение информации из заранее подготовленного файла.
Для работы с файлом при помощи метода new создается экземпляр класса File. Обязательным аргументом этого метода является строка, содержащая имя файла, например,
f = File.new("myfile.txt")
Другим (необязательным) аргументом является задание режима работы с файлом. По умолчанию этот параметр имеет значение "r", что соответствует режиму "только чтение". Если требуется открыть файл с возможностью записи в него, то следует указать параметр "w", например,
f1 = File.new("newfile.txt", "w")
Метод readlines считывает весь файл, создает массив и размещает каждую прочитанную строку в отдельном элементе массива При дальнейшей обработке полученного массива удобно использовать метод each.
Для вывода строки в выходной поток (в файл или на экран монитора) используется метод write, например,
a = "Hello, world!" f1.write(a)
Задача
Имеется текстовый файл fio.txt, содержащий список фамилий, имен и отчеств учащихся. При этом каждая строка файла содержит данные только об одном человеке, например,
Петров Сергей Васильевич Сидорова Ольга Петровна Иванова Марья Даниловна
Напишите программу, которая читает информацию из файла и
печатает пронумерованный список учеников;печатает пронумерованный список фамилий и инициалов.
Решение 1
f = File.new("fio.txt") n = 1 student = f.readlines student.each{ |i| print n, ". ", i n += 1 }
Отметим, что программа должна располагаться в той же директории, что и файл с данными. В противном случае необходимо указывать полный путь к этому файлу.
Для получения инициалов каждую строку полученного массива преобразуем в массив, элементами которого будут фамилия, имя и отчество. Затем фамилию печатаем полностью, а вместо следующих элементов массива - только их первый символ. Для преобразования строки в массив используется ранее рассмотренная функция split. Напомним, что параметром по умолчанию этой функции является пробел.
Решение 2
f = File.new("fio.txt") n = 1 student = f.readlines student.each{ |i| i.chop! fio = i.split print n, ". ", fio[0], " ", fio[0][0].chr, ". ", fio[1][0].chr, ".\n" n += 1 }
Пример 1.14.
(html, txt)
Разработка пользовательских классов
Пример программы на языке Ruby, демонстрирующий работу с классами, уже приводился в глава 9. Следующий пример демонстрирует использование так называемой переменной класса, которая не принадлежит ни одному из экземпляров данного класса, а используется для хранения информации, относящейся ко всему классу в целом.
Задача
Напишите программу, описывающую класс автомобиль и два его дочерних класса: спортивные машины и машины для семейного использования. В программе нужно предусмотреть возможность печати общего числа созданных автомобилей.
Решение
Поместите в файл с именем car.rb следующую программу:
class Car @@NUM_CARS = 0 def initialize @@NUM_CARS = @@NUM_CARS + 1 puts @@NUM_CARS end end class SportsCar < Car end class FamilyCar < Car end
a = Car.new b = SportsCar.new c = FamilyCar.new
Для запуска программы выполните команду ruby car.rb. При создании каждого автомобиля, независимо от того, к какому (родительскому или дочернему) классу он принадлежит, значение переменной класса @@NUM_CARS увеличивается на единицу.
Пример 1.16.
(html, txt)
Задания
Напишите программу, запрашивающую с клавиатуры натуральное число, большее 1, и печатающую список всех простых несократимых дробей, заключенных в интервале между 0 и 1, знаменатели которых не превышают введенное число. Например, если ввести число 4, то должна быть напечатана последовательность 1/2, 1/3, 2/3, 1/4, 3/4. Подсказка: используйте функцию нахождения НОД.Создайте текстовый файл, в котором разместите фамилии учащихся и их рост в сантиметрах. Напишите программу печатающую фамилию и рост самых высоких учеников;по введенному числу - росту с сантиметрах - печатающую список всех учащихся, чей рост не превышает введенного числа.Напишите программу, вычисляющую методом Монте-Карло площадь криволинейной трапеции, ограниченной графиками функций y=sin(x) и y=0 (x изменяется в интервале от 0 до PI).

 | © 2003-2007 INTUIT.ru. Все права защищены. |
Случайные числа
Моделирование случайных процессов на компьютере - достаточно распространенное явление. Как и в большинстве языков программирования в Ruby есть методы, генерирующие, так называемые, "псевдослучайные" числа (их нельзя считать чисто случайными, ведь создаются они при помощи некоторого алгоритма).
Для получения случайного целого числа в диапазоне от 0 до n используется метод rand(n). Случайное число в диапазоне от 0 до 1 получается с помощью этого же метода без указания параметра.
a1 = (1..10).collect { |j| rand(100)} a2 = (1..4).collect { |j| rand()} p a1, a2
Ниже представлен возможный вывод:
[64, 17, 21, 95, 58, 24, 29, 60, 47, 63] [0.2009671596, 0.8890923676, 0.3349569312, 0.8719313448]
Одним из применений случайных чисел является компьютерное моделирование метода Монте-Карло для определения площади некоторой фигуры, рассмотренный нами ранее. Напомним, что для применения этого метода фигуру вписывают в другую, известной площади, и случайным образом "бросают" точки, подсчитывая число попаданий в фигуру. При достаточно большом числе испытаний отношение числа точек, попавших внутрь фигуры, к общему числу точек, стремится к отношению их площадей.
Задача
Напишите программу, вычисляющее приближенное значение числа PI при помощи метода Монте-Карло.
Решение
Число PI равно отношению площади круга к квадрату его радиуса. Впишем круг единичного радиуса с центром в начале координат в квадрат и методом Монте-Карло найдем его площадь. Координаты случайных точек, бросаемых в круг, принадлежат интервалу (-1; 1). Величина, случайно распределенная в этом интервале, задается выражением 2*rand() - 1.
Для контроля за временем добавим два экземпляра класса Time: время начала и окончания расчета. Программа, реализующая этот алгоритм, представлена ниже. В ней используется оператор eval, чтобы количество точек можно было задавать в виде арифметического выражения.
puts "Введите количество точек:" n1, n, t1 = 0, eval(gets.chop), Time.now for i in 1 .. n x = 2*rand() - 1 y = 2*rand() - 1 # проверяем попадание внутрь круга n1 += 1 if (x**2 + y**2) < 1 end puts "PI=#{4.0*n1/n}" t2 = Time.now puts "Число точек #{n}, время расчета " + "около #{(t2 - t1).round} сек."
Возможные результаты работы программы будут похожи (случайность!) на следующие:
Введите количество точек: 10**5 PI=3.14028 Число точек 100000, время расчета около 2 сек.
Введите количество точек: 10**6 PI=3.142204 Число точек 1000000, время расчета около 20 сек.
Пример 1.15.
(html, txt)
Строки
Другим столь же распространенным классом является класс String. К этому классу относятся произвольные строки символов, заключенные в апострофы или кавычки, например, 'hello', 'раз, два, три', "привет всем". Есть несколько альтернативных способов задания каждого из этих видов строк.
Для задания строки в апострофах можно использовать любой из способов представленных ниже.
puts 'hello' # hello puts %q/hello/ # hello puts %q(hello) # hello
Два подряд идущих символа \ внутри такой строки заменяются на один.
puts 'hell\\o' # hell\o puts %q(hell\\o) # hell\o
Для того чтобы внутрь строки, заключенной в апострофы, вставить апостроф, следует предварительно "экранировать" его символом \ (обратный слеш).
puts 'hell\'o' # hell'o puts %q(hell\'o) # hell\'o puts 'hel"l"o' # hel"l"o
Для создания строки, заключенной в кавычки, следует либо просто заключить ее в кавычки, либо использовать конструкции %Q или %, после которых указывается строка, обрамленная с двух сторон одним и тем же символом, отличным от цифр и букв (можно использовать также пару любых скобок). Ниже перечислено несколько способов задания строки "hello".
"hello" %Q/hello/ %Q{hello} %Q(hello) %Q!hello! %<hello> %(hello) %!hello! %*hello* %+hello+
puts "Say \"Hello\"" # Say "Hello"
Строка, заключенная в кавычки, позволяет интерпретировать последовательности символов, начинающиеся с символа \ такие, например, как \n (символ перехода на новую строку) и \t (табуляция). Другой особенностью строк, заключенных в кавычки, является возможность использования подстановки: если строка содержит некоторое выражение, ограниченное символами #{ и }, то оно заменяется на результат его вычисления. Добавьте в программу следующие строки и проанализируйте полученный вывод.
puts "a \t b"; puts 'a \t b' puts "выражение 3*5+8 равно #{3*5+8}" puts 'выражение 3*5+8 равно #{3*5+8}' puts "работа с целыми числами: 5/8 = #{5/8}" puts "перевод в класс Float: 5/8 = #{5/8.to_f}"
К строкам могут применяться методы to_i и to_f. При преобразовании к целому числу отбрасывается оставшаяся часть строки, как только встречается символ, отличный от цифры (исключение - знак плюс или минус в первой позиции строки). Аналогичные правила применяются и при преобразовании к дробному числу. Единственным отличием является то, что первая найденная точка рассматривается как разделитель между целой и дробной частями. Следующий фрагмент иллюстрирует сказанное:
puts "-12.34".to_i puts "12.34".to_f puts "+12:34".to_i puts "12qq34".to_f
Для получения строки, содержащей символ с заданным ASCII кодом, используется метод chr, например,
puts 209.chr
Следует помнить, что этот метод может быть применен только к положительному целому числу, не превышающему 255.
Класс String предоставляет большое число методов для работы со строками, некоторые из которых представлены в следующей таблице.
| + | Сцепление строк "мол" + "око" | "молоко" |
| * | Повтор строки "ab" * 3 | "ababab" |
| [ ] | Возвращает ASCII-код символа, находящегося на указанной позиции строки (отсчет начинается с нуля) "abcdef"[0] "abcdef"[0].chr | 97 "a" |
| [нач..кон] | Возвращает подстроку, заключенную в указанном диапазоне (включая концы) "abcdef"[0..3] | "abcd" |
| [нач, дл] | Возвращает подстроку, начинающуюся с указанной позиции и имеющую заданную длину "abcdef"[0,3] | "abc" |
| capitalize | Заменяет первый символ строки (если он является буквой латинского алфавита) на заглавную "abc".capitalize | "Abc" |
| chop | Удаляет указанные символы из строки, может указываться диапазон изменения символов "abcdef".delete('ea') "abcdef".delete('a-c') | "bcdf" "def" |
| index | Определяет номер позиции, с которой начинается указанная подстрока; можно указывать номер позиции, с которой начинается поиск "abcdabcd".index("cd") "abcdabcd".index("cd",3) | 2 6 |
| length size | Определяют длину строки (в байтах) "12345678".length "12345678".size | 8 8 |
| ljust rjust center | Дополняют строку пробелами до указанной ширины, выравнивая соответственно по левому краю, по правому краю или по центру "123".ljust(8) "123".rjust(8) "123".center(8) | "123 " " 123" " 123 " |
| reverse | Возвращает строку, содержащую символы в обратном порядке "1234567".reverse | "7654321" |
| strip | Удаляет пробелы в начале и конце строки " 123 ".strip | "123" |
| squeeze | Оставляет в группе повторяющихся символов только один; допускается задание списка символов, на которых распространяется данное действие "22---23**".squeeze "22---23**".squeeze('*-') | "2-23*" "22-23*" |
| tr | Заменяет все найденные вхождения символов на заданные "22+33=55".tr('25','47') | "44+33=77" |
puts eval("2**10") puts eval(""мол".size * "око".size') # 9
Пример 1.3.
(html, txt)
Отдельного упоминания заслуживает метод eval, позволяющий динамически выполнять другие методы. Этот метод анализирует переданную ему строку, рассматривая ее как часть программы, и выполняет ее. Обратите внимание, что при вызове этого метода используется не точечная, а функциональная форма записи:
puts eval("2**10") puts eval(""мол".size * "око".size') # 9#!/usr/bin/env ruby
puts 'hello' # hello puts %q/hello/ # hello puts %q(hello) # hello
puts 'hell\\o' # hell\o puts %q(hell\\o) # hell\o
puts 'hell\'o' # hell'o puts %q(hell\'o) # hell\'o puts 'hel"l"o' # hel"l"o
puts "hello" puts %Q/hello/ puts %Q!hello! puts %Q{hello} puts %Q(hello) puts %Q!hello! puts %<hello> puts %!hello! puts %*hello* puts %+hello+ puts %(hello)
puts "Say \"Hello\"" # Say "Hello" puts "Say 'Hello'" # Say 'Hello'
puts "a \t b" puts 'a \t b' puts "выражение 3*5+8 равно #{3*5+8}" puts 'выражение 3*5+8 равно #{3*5+8}' puts "работа с целыми числами: 5/8 = #{5/8}" puts "перевод в класс Float: 5/8 = #{5/8.to_f}"
puts "-12.34".to_i puts "12.34".to_f puts "+12:34".to_i puts "12qq34".to_f
puts 209.chr
puts "123456789".reverse puts " 123 " puts " 123 ".strip puts "---22--23****".squeeze('*-') puts "---22--23****".squeeze
puts "Дашка любит молоко, а Танька - квас".tr('ДТ','МД') puts "22+33=55".tr('25','47')
puts "abcdef"[0].chr puts "abcdef".chop puts "abcdef".chop.chop puts "abcdef".delete("ea") puts "abcdef".delete('a-c') puts "abcdefabcdef".length puts "12345678".size
puts "ABCDEF".downcase puts "abcdef".index("cd") puts "abcdefabcdef".index("cd",3)
a="12345" puts "12345"[3].chr puts "12345"[0..3] puts "12345"[0,3]
puts "привет".capitalize # Не работает с русскими буквами! puts "abcdabcd".index("cd",3) puts "*"+"123".ljust(9)+*" puts "*"+"123".center(9)+"*" puts "*"+"123".rjust(9)+"*"
puts (eval "2**10") puts (eval ""мол".size * "око".size')
=begin s="2*3+4" puts s puts "#{s}" puts eval(s) puts eval s
puts s.eval # Ошибка! Неправильный вызов метода
print "Введите команды:" eval gets.chop! =end
Пример 1.3.
Время и дата
Экземпляр класса Time в языке Ruby содержит информацию о дате, времени и временной зоне. Для создания объекта этого класса, содержащего текущие дату и время, используется метод now. Такие объекты могут являться аргументами операций + и -:
puts Time.now puts Time.now+60 # добавили 60 секунд к текущему времени puts Time.now-60 # отняли 60 секунд от текущего времени
Отметим некоторые методы этого класса, для вызова которых используется точечная нотация.
| sec | Получить число секунд |
| min | Получить число минут |
| hour | Получить число часов |
| mday и day | Получить день месяца |
| mon и month | Получить номер месяца |
| year | Получить год |
| wday | Получить номер дня недели |
| yday | Получить номер дня в году |
| zone | Получить информацию о временной зоне |
| to_i | Получить число секунд, прошедших с 1 января 1970 года |
В языке Ruby имеется метод sleep, который заставляет программу "заснуть" на число секунд, указанное в качестве аргумента метода. Посмотрите на пример использования методов для работы с объектами класса Time.
puts "До Нового года осталось #{365-Time.now.yday} дней" puts Time.now puts "Подождем 10 секунд." sleep(10) puts Time.now
Пример 1.4.
(html, txt)
Вывод данных
Мы уже видели, как осуществляется вывод информации в Ruby. Познакомимся с другими операторами, обеспечивающими печать данных. Создайте файл print.rb, включите в него следующий текст и посмотрите на результат выполнения полученной программы.
puts "puts всегда завершается переходом к новой строке." print "А оператор print не делает этого по умолчанию, " print "как вы видите в этом примере.\n" print "print может быть вызван сразу ", "с несколькими аргументами.\n"
Оператор p подобен оператору puts и отображает объекты в виде, понятном человеку. Не следует использовать его для вывода русских букв - он печатает их ASCII-коды.
p Time.now, Time.now+3600
Значительно большими возможностями обладает оператор printf, обеспечивающий форматный вывод. Сразу после имени оператора указывается строка формата, содержащая как обычные символы, выводимые на печать, так и спецификации преобразования, которые вызывают преобразование и печать остальных аргументов в том порядке, в каком они перечислены. Каждая спецификация преобразования начинается с символа % и заканчивается символом-спецификатором преобразования. Между % и символом-спецификатором в порядке, указанным ниже, могут располагаться следующие модификаторы:
флаги (в любом порядке):
- указывает на то, что преобразованный аргумент должен быть прижат к левому краю поля;
+ предписывает всегда печатать число со знаком;
0 - указывает, что числа должны дополняться ведущими нулями до всей ширины поля;
пробел - указывает, что числа должны дополняться ведущими нулями до всей ширины поля;
число, задающее минимальную ширину поля;точка, отделяющая указатель ширины поля от указателя точности;число, задающее точность.
Основные литеры-спецификаторы и разъяснение их смысла приводятся в следующей таблице.
| d | Fixnum, Bignum | печать целого числа |
| s | String | печать строки |
| f | Float | печать дробного числа |
Включите в файл следующие операторы форматной печати и посмотрите на результаты выполнения:
printf "%8s~~%-8s\n", "abcd", "abcd" printf "%8-s::%8s\n", "abcd", "abcd" printf "%06d\n", 2**10; printf "%+6d\n", 2**10 printf "%6d\n", 2**10; printf "%+6d\n", 2.5*1.3 printf "%4.3f\n", 2.5*1.3 printf "-2/7=%+1.6f, -2/6=%2.15f\n", -2/7.to_f, -2/6.to_f
Обратите внимание, что строка формата заключается в двойные кавычки и может содержать специальные последовательности символов. Одной из них является \n. Эта последовательность дает указание интерпретатору Ruby продолжить вывод информации со следующей строки (newline). Другой часто используемой последовательностью является \t (табуляция), которая передвигает фокус вывода к следующей позиции табуляции.
puts "*\t*\t*\t*\t*" puts " 1234567 1234567 1234567 1234567 "
Пример 1.5.
(html, txt)
printf "%8s~~%-8s\n", "abcd", "abcd" printf "%8-s::%8s\n", "abcd", "abcd" printf "%06d\n", 2**10; printf "%+6d\n", 2**10 printf "%6d\n", 2**10; printf "%+6d\n", 2.5*1.3 printf "%4.3f\n", 2.5*1.3 printf "-2/7=%+1.6f, -2/6=%2.15f\n", -2/7.to_f, -2/6.to_f
Обратите внимание, что строка формата заключается в двойные кавычки и может содержать специальные последовательности символов. Одной из них является \n. Эта последовательность дает указание интерпретатору Ruby продолжить вывод информации со следующей строки (newline). Другой часто используемой последовательностью является \t (табуляция), которая передвигает фокус вывода к следующей позиции табуляции.
puts "*\t*\t*\t*\t*" puts " 1234567 1234567 1234567 1234567 "#!/usr/bin/env ruby puts "puts всегда завершается переходом к новой строке." print "А оператор print не делает этого по умолчанию, " print "как вы видите в этом примере.\n" print "print может быть вызван сразу ", "с несколькими аргументами.\n"
p Time.now, Time.now+3600
printf "%8s~~%-8s\n", "abcd", "abcd" printf "%8-s::%8s\n", "abcd", "abcd" printf "%06d\n", 2**10; printf "%+6d\n", 2**10 printf "%6d\n", 2**10; printf "%+6d\n", 2.5*1.3 printf "%4.3f\n", 2.5*1.3 printf "-2/7=%+1.6f, -2/6=%2.15f\n", -2/7.to_f, -2/6.to_f
puts "*\t*\t*\t*\t*" puts " 1234567 1234567 1234567 1234567 "
Пример 1.5.