АБСТРАКТНЫЙ АЛФАВИТ

Информация передается в виде сообщений. Дискретная информация записывается с помощью некоторого конечного набора знаков, которые будем называть буквами, не вкладывая в это слово привычного ограниченного значения (типа «русские буквы» или «латинские буквы»). Буква в данном расширенном понимании - любой из знаков, которые некоторым соглашением установлены для общения. Например, при привычной передаче сообщений на русском языке такими знаками будут русские буквы - прописные и строчные, знаки препинания, пробел; если в тексте есть числа - то и цифры. Вообще, буквой будем называть элемент некоторого конечного множества (набора) отличных друг от друга знаков. Множество знаков, в котором определен их порядок, назовем алфавитом (общеизвестен порядок знаков в русском алфавите: А, Б,..., Я).

Рассмотрим некоторые примеры алфавитов.

1, Алфавит прописных русских букв:

А Б В Г Д Е Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ъ Ы Ь Э Ю Я

2. Алфавит Морзе:

3. Алфавит клавиатурных символов ПЭВМ IBM (русифицированная клавиатура):

4. Алфавит знаков правильной шестигранной игральной кости:

5. Алфавит арабских цифр:

0123456789

6. Алфавит шестнадцатиричных цифр:

0123456789ABCDEF

Этот пример, в частности, показывает, что знаки одного алфавита могут образовываться из знаков других алфавитов.

7. Алфавит двоичных цифр:

0 1

Алфавит 7 является одним из примеров, так называемых, «двоичных» алфавитов, т.е. алфавитов, состоящих из двух знаков. Другими примерами являются двоичные алфавиты 8 и 9:

8. Двоичный алфавит «точка, «тире»:. _

9. Двоичный алфавит «плюс», «минус»: + -

10. Алфавит прописных латинских букв:

ABCDEFGHIJKLMNOPQRSTUVWXYZ

11. Алфавит римской системы счисления:

I V Х L С D М

12. Алфавит языка блок-схем изображения алгоритмов:

13. Алфавит языка программирования Паскаль (см. в главе 3).

АДРЕСАЦИЯ ДАННЫХ

Теперь, когда мы знаем практически все об операционной части команды, можно заняться адресной. Посмотрим, какими способами могут представляться операнды ОП1 иОП2.

Начнем с того, что под кодирование каждого операнда всегда отводится четыре двоичных разряда. Из них старшие два будут всегда задавать тип адресации данных. а младшие - его конкретизировать. В большинстве случаев два младших бита будут просто представлять собой номер регистра, с участием которого осуществляется адресация.

Старшая «половинка» модификатора операнда, соответствующая типу адресации, может содержать четыре неповторяющиеся двоичные комбинации:

00 - регистровый

метод адресации: операнд является содержимым указанного регистра;

01 - метод косвенной адресации: операндом является содержимое ячейки ОЗУ, адрес которой задан в указанном регистре;

10 - резерв; в будущей версии здесь будет реализован индексный метод адресации;

11 - адресация по счетчику адреса команд

PC: операнд извлекается с использованием информации, входящей в команду (более подробные объяснения приведены ниже).

Рассмотрим перечисленные способы адресации подробнее.

Наиболее простым является регистровый метод, который мы фактически уже использовали в примерах предыдущего раздела. Учитывая, что этому методу соответствуют нулевые значения старших битов, полный код операнда совпадает с номером регистра: двоичная комбинация 0000 соответствует R0, 0001 - R1 и т.д.

В качестве данных для операции используется информация, содержащаяся в указанном регистре. Например, если Rl = 3, а R2 = 5, то в результате выполнения команды

0212:R2+R1=>R2

получится R2 = 8.

При косвенной

адресации код операнда выглядит несколько сложнее: косвенное обращение по регистру R0 имеет вид 0100 (т.е. 4), по Rl - 0101 (5) и т.д. Содержимое указанного регистра при этом служит не операндом, а его адресом в ОЗУ. Рассмотрим команду

0263: R3 + (R2) => R3

где скобки у R2 символизируют косвенную адресацию. Пусть содержимое R2 в данный момент равно 30, а R3 = 6.
Примем также, что в ячейке памяти с адресом 30 хранится число 10. Тогда процессор «Е97», выполняя команду, к имеющемуся в R3 значению 6 прибавит число из ячейки 30, на которую указывает R2, и результат операции - 16 - занесет в R3.

И, наконец, рассмотрим способы адресации по программному счетчику PC. Поскольку в этом случае регистр, по которому производится адресация, уже однозначно определен, освобождаются два младших бита операнда, которые можно использовать для других целей. В связи с этим удается получить четыре различных способа адресации по счетчику:

11 00 - резерв;

11 01 - операндом служит константа, входящая в команду;

11 10 - операнд извлекается из ячейки ОЗУ, адрес которой входит в команду;

1111-резерв.

Итак, в «Е97» существует два метода адресации по PC, соответствующих шест-надцатеричным кодам D и Е в качестве операнда. Изучим их на примерах. Команда, состоящая из двух слов

02D1

0020

выполняет операцию Rl + 20 => Rl следующим образом: к текущему значению Rl прибавляется извлеченное из команды число 20 и результат помещается в Rl. Если первоначальное значение Rl было, скажем, F0, то в результате операции в Rl запишется 110.

Рассмотрим еще одну команду с адресацией по PC:

021Е

0020

выполняющую операцию (20) + Rl => (20) так: к числу, хранящемуся в ячейке памяти 20, прибавляется значение Rl. В случае, когда Rl = F0, a (20) = 40, ответ будет: (20)= 130.

На этом рассказ о методах адресации можно было бы и закончить, если бы не наличие в командах модификатора, хранящегося в первой цифре шестнадцатерич-ного представления команды. Его значение также может существенно влиять на извлечение данных и запись результата.

Во всех приведенных в данном пункте примерах МОД = 0 и, следовательно, не оказывает влияния на расшифровку и выполнение операции. Если же он имеет ненулевое значение, необходимо дополнительно учитывать и этот фактор.

Модификатор состоит из четырех битов, причем два старших отвечают за «переключением бант/слово, а два младших - за особый способ представления данных, называемый «короткой константой».

АЛГОРИТМ ВЫПОЛНЕНИЯ ПРОГРАММ НА ПРОЛОГЕ

Факты и правила программы на Прологе являются описанием отношений и связей между объектами некоторой предметной области, т.е. записью условия некой логической задачи, которую предстоит решить. Описанные отношения и связи рассматриваются статически. Такой подход к программе называется декларативным. Порядок следования фактов, правил и подцелей в правилах не влияет на декларативный смысл программы.

Вместе с тем, программу можно рассматривать с точки зрения последовательности сопоставлений, конкретизации переменных и резолютивных выводов, происходящих при ее выполнении. Такой подход называется процедурным. Процедурный смысл программы обязательно должен учитываться при программировании на Прологе. Так, факт можно рассматривать как полностью определенную процедуру, для выполнения которой больше ничего не нужно. Правило

А:-В1,В2,...,Вn.

можно рассматривать как определение процедуры А, утверждающее, что для ее выполнения надо определить Bl, B2, ... , Вn. Процедуры Bl, B2, ... , Вn должны выполняться в определенном порядке - слева направо. Если выполнение очередной процедуры завершается успешно, то происходит переход к следующей процедуре. Если же по какой-либо причине очередная процедура выполняется неуспешно, то происходит переход к следующему варианту описания этой процедуры, и порядок поиска такого варианта в Прологе задан - сверху вниз. Поиск подходящих для согласования фактов и правил в базе знаний происходит последовательно сверху-вниз, и если подходящих фактов не найдено - ответ отрицательный. Эта стратегия согласования называется «сверху-вниз» и «замкнутый мир».

Рассмотрим процесс выполнения программы более подробно на примере.

Программа 112

а : - b, с, d.

b : - е, f.

с. d. е. f.

? - а.

Выполнение программы начинается с применения метода резолюций к целевому и одному из предложений программы для получения их резольвенты. Подходящее предложение программы подбирается перебором сверху-вниз так, чтобы сопоставление его заголовка с целевым предложением было успешным.
В результате резолюции получается новое целевое предложение и метод резолюции применяется к нему и к другому предложению программы. Процесс продолжается до тех пор, пока не будут согласованы с фактами все возникшие при резолюции подцели, табл. 3.6.

Таблица 3.6

К процессу выполнения программы на Прологе

Номер шага резолюции		Целевое предложение	Исходное предложение	Резольвента
1		?-а.	a:-b,c,d.	?-b,c,d.
2		?-b,c,d.	b:-c,f.	?-e,f,c,d.
3			?-е,f,с,d	e.       ?-f,c,d.
4			?-f,c,d.	f.        ?-c.d.
5			?-c,d.	c.        ?-d.
6			?-d.	d.       Пустая

При выполнении логического вывода, если необходимо, происходит конкретизация переменных. Рассмотрим пример.

Программа 113

любит(юрий,музыку).

любит(сергей,спорт).

любит(А,книги):-читатель(А),любопытный(А).

любит(сергей,книги).

любит(сергей,кино).

читатель(юрий).

любопытный(юрий).

?- любит(X,музыку), любит(X,книги).

Двойной запрос в этой программе может быть представлен целевым деревом:



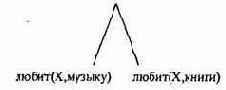
Вначале, просматривая программу сверху вниз. Пролог находит первое предложение, соответствующее первой подцели запроса:



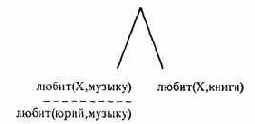
Переменная Х конкретизируется значением «юрий». Начинается согласование 2-й подцели запроса с условием Х=юрий. 1-е и 2-е предложения программы не соответствуют подцели. В 3-ем предложении:

любит(А,книги):-читатель(А), любопытный(А).

аргумент А заголовка есть переменная, поэтому она может соответствовать X, т.е. получает значение А=юрин; вторые аргументы совпадают. Теперь тело правила образует новое множество целей для согласования. Получаем целевое дерево:





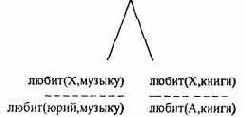
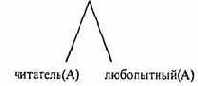
Затем Пролог будет искать факты, соответствующие новым подцелям. Последнее результирующее дерево:





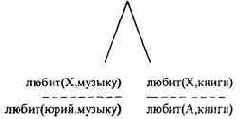
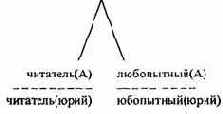
Рассмотрим еще один пример.

Программа 114

любит(оля,чтение).

любит(света,бадминтон).

любит(для,бадминтон).

любит(лена,плавание).



любит(лена,чтение).

?- любит(X,чтение), любит(X,плавание).

Запрос означает: есть ли люди, которым нравится и чтение, и плавание? Сначала Пролог ищет факт, сопоставимый с первой частью вопроса: любит(Х, чтение). Подходит первый же факт программы

любит(оля,чтение).

и переменная Х связывается значением «оля». В то же время Пролог фиксирует в списке фактов указатель, показывающий состояние процедуры поиска. Далее Пролог пытается согласовать вторую часть запроса при условии Х = оля, т.е. ищет с самого начала программы факт «любит(оля, плавание)». Такого факта в программе нет, и поиск заканчивается неуспешно. Тогда Пролог возвращается к первои части запроса: любнт(Х,чтение) , «развязывает» переменную Х и продолжает поиск подходящих фактов, начиная с ранее установленного в списке фактов указателя Подходит факт «любит(лена,чтение)», переменная Х конкретизируется значением «лена», и далее вторая часть вопроса успешно согласуется с фактом «любит(лена, плавание)». Пролог выполнил в данном примере поиск с возвратом.

Графически процесс выполнения программы представляется в виде обхода бинарного дерева - дерева вывода, типа изображенного на рис.3.16. Вершины дерева обозначают вопросы, а ребра показывают возможные пути вывода, причем для каждого ребра характерны свои правила и унифицирующая подстановка значений переменных.



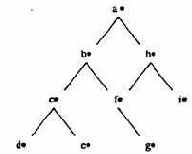
Рис.3.16. Дерево вывода программы на Прологе

Обход дерева начинается с движения от вершины (запроса) по самой левой ветви вниз до конца (abed), при этом запоминаются все точки ветвления (точки возврата). При достижении конца ветви решение будет либо найдено, либо нет. В обоих случаях Пролог продолжает дальнейший поиск решений. Выполняется возврат в последнюю точку ветвления с. При этом конкретные значения, присвоенные переменным при движении вниз на сегменте c-d. отменяются, и движение вниз продолжается по расположенной справа ветви с-е до конца дерева вниз. Затем произойдет возврат в предыдущую точку ветвления b и движение продолжится по ветви bfg, и так до тех пор, пока все дерево вывода не будет пройдено.

АНТИВИРУСНЫЕ СРЕДСТВА

К настоящему времени накоплен значительный опыт борьбы с компьютерными вирусами, разработаны антивирусные программы, известны меры защиты программ и данных. Происходит постоянное совершенствование, развитие антивирусных средств, которые в короткий срок с момента обнаружения вируса -от недели до месяца - оказываются способными справиться с вновь появляющимися вирусами.

Создание антивирусных программ начинается с обнаружения вируса по аномалиям в работе компьютера. После этого вирус тщательно изучается, выделяется его сигнатура - последовательность байтов, которая полностью характеризует программу вируса (наиболее важные и характерные участки кода), выясняется механизм работы вируса, способы заражения. Полученная информация позволяет разработать способы обнаружения вируса в памяти компьютера и на магнитных -дисках, а также алгоритмы обезвреживания вируса (если возможно, удаления вирусного кода из файлов - «лечения»).

Известные ныне антивирусные программы можно разделить на несколько типов, перечисленных ниже.

• Детекторы. Пх назначение - лишь обнаружить вирус. Детекторы вирусов могут сравнивать загрузочные сектора дискет с известными загрузочными секторами, формируемыми операционными системами различных версий, и таким образом обнаруживать загрузочные вирусы или выполнять сканирование файлов на магнитных дисках с целью обнаружения сигнатур известных вирусов. Такие программы в чистом виде в настоящее время редки.

• Фаги. Фаг - это программа, которая способна не только обнаружить, но и уничтожить вирус, т.е. удалить его код из зараженных программ и восстановить их работоспособность (если возможно). Известнейшим в России фагом является Aidstest, созданный Д.Лозинским. К январю 1997 года эта программа была способна обнаружить и обезвредить около 1600 вирусов. Еженедельно появляются новые версии этой программы, рассчитанные на обезвреживание десятков новых вирусов.

Очень мощным и эффективным антивирусным средством является фаг Doctor Web (созданный И.Даниловым). Детектор этого фага не просто сканирует файлы в поисках одной из известных вирусных сигнатур.
Doctor Web реализует эвристический метод поиска вирусов, может находить и обезвреживать, так называемые, полиморфные вирусы (не имеющие определенной сигнатуры), проверять файлы, находящиеся в архивах. Для нахождения вирусов Doctor Web использует программную эмуляцию процессора, т.е. он моделирует выполнение остальных файлов с помощью программной "модели микропроцессора 1-8086 и тем самым создает среду для проявления вирусов и их размножения. Таким образом, программа Doctor Web может бороться не только с полиморфными вирусами, но и с вирусами, которые только еще могут появиться в перспективе. Специалисты рекомендуют использовать Aidstest и Doctor Web в комплексе.

• Ревизоры. Программа-ревизор контролирует возможные пути распространения программ-вирусов и заражения компьютеров. Программы-ревизоры относятся к самым надежным средствам защиты от вирусов и должны входить в арсенал каждого пользователя. Ревизоры являются единственным средством, позволяющим следить за целостностью и изменениями файлов и системных областей магнитных дисков. Наиболее известна в России программа-ревизор ADinf, разработанная Д.Мостовым.

• Сторожа. Сторож - это резидентная программа, постоянно находящаяся в памяти компьютера, контролирующая операции компьютера, связанные с изменением информации на магнитных дисках, и предупреждающая пользователя о них. В состав операционной системы MS DOS, начиная с версии 6.0, входит сторож VSAFE. Однако, из-за того, что обычные программы выполняют операции, похожие на те, что делают вирусы, пользователи обычно не используют сторожа, так как постоянные предупреждения мешают работе.

• Вакцины. Так называются антивирусные программы, ведущие себя подобно вирусам, но не наносящие вреда. Вакцины предохраняют файлы от изменении и способны не только обнаружить факт заражения, но и в некоторых случаях «вылечить» пораженные вирусами файлы. В настоящее время антивирусные программы-вакцины широко не применяют, так как в прошлые годы некоторыми некорректно работающими вакцинами был нанесен ущерб многим пользователям.



Помимо программных средств защиты от вирусов существуют и специальные дополнительные устройства, обеспечивающие надежную защиту определенных разделов винчестера. Примером такого рода устройств является плата Sheriff (разработанная Ю.Фоминым). Несмотря на кажущееся обилие программных антивирусных средств, даже все вместе они не обеспечивают полной защиты программ и данных, не дают 100%-ной гарантии от воздействия вирусных программ. Только комплексные профилактические меры защиты обеспечивают надежную защиту от возможной потери информации. В комплекс таких мер входит:

• регулярное архивирование информации (создание резервных копий важных файлов и системных областей винчестера);

• избегание использования случайно полученных программ (старайтесь пользоваться только законными путями получения программ);

• входной контроль нового программного обеспечения, поступивших дискет;

•сегментация жесткого диска, т.е. разбиение его на логические разделы с разграничением доступа к ним;

• систематическое использование программ-ревизоров для контроля целостности информации;

• при поиске вирусов (который должен происходить регулярно!) старайтесь использовать заведомо чистую операционную систему, загруженную с дискеты. Защищайте дискеты от записи, если есть хоть малая вероятность заражения.

При неаккуратной работе с антивирусными программами можно не только переносить с ними вирусы, но и вместо лечения файлов безнадежно их испортить. Полезно иметь хотя бы общее представление о том, что могут и чего не могут компьютерные вирусы, об их жизненном цикле, о важнейших методах защиты.

АППАРАТНЫЕ СРЕДСТВА

Локальные сети (ЛС ЭВМ) объединяют относительно небольшое число компьютеров (обычно от 10 до 100, хотя изредка встречаются и гораздо большие) в пределах одного помещения (учебный компьютерный класс), здания или учреждения (например, университета). Традиционное название - локальная вычислительная сеть (ЛВС) - скорее дань тем временам, когда сети в основном использовались для решения вычислительных задач; сегодня же в 99% случаев речь идет исключительно об обмене информацией в виде текстов, графических и видео-образов, числовых массивов. Полезность ЛС объясняется тем, что от 60% до 90% необходимой учреждению информации циркулирует внутри него, не нуждаясь в выходе наружу.

Большое влияние на развитие ЛС оказало создание автоматизированных систем управления предприятиями (АСУ). АСУ включают несколько автоматизированных рабочих мест (АРМ), измерительных комплексов, пунктов управления. Другое важнейшее поле деятельности, в котором ЛС доказали свою эффективность -создание классов учебной вычислительной техники (КУВТ).

Благодаря относительно небольшим длинам линий связи (как правило, не более 300 метров), по ЛС можно передавать информацию в цифровом виде с высокой скоростью передачи. На больших расстояниях такой способ передачи неприемлем из-за неизбежного затухания высокочастотных сигналов, в этих случаях приходятся прибегать к дополнительным техническим (цифро-аналоговым преобразованиям) и программным (протоколам коррекции ошибок и др.) решениям.

Характерная особенность ЛС - наличие связывающего всех абонентов высокоскоростного канала связи для передачи информации в цифровом виде. Существуют проводные и беспроводные (радио) каналы. Каждый из них характеризуется определенными значениями существенных с точки зрения организации ЛС параметров:

• скорости передачи данных;

• максимальной длины линии;

• помехозащищенности;

• механической прочности;

• удобства и простоты монтажа;

• стоимости.

В настоящее время обычно применяют четыре типа сетевых кабелей:

• коаксиальный кабель;

• незащищенная витая пара;

• защищенная витая пара;

• волоконно-оптический кабель.

Первые три типа кабелей передают электрический сигнал по медным проводникам. Волоконно-оптические кабели передают свет по стеклянному волокну.

Большинство сетей допускает несколько вариантов кабельных соединений.

Коаксиальные кабели состоят из двух проводников, окруженных изолирующими слоями. Первый слой изоляции окружает центральный медный провод. Этот слой оплетен снаружи внешним экранирующим проводником. Наиболее распространенными коаксиальными кабелями являются толстый и тонкий кабели «Ethernet». Такая конструкция обеспечивает хорошую помехозащищенность и малое затухание сигнала на расстояниях.

Различают толстый (около 10 мм в диаметре) и тонкий (около 4 мм) коаксиальные кабели. Обладая преимуществами по помехозащищенности, прочности, длине линий, толстый коаксиальный кабель дороже и сложнее в монтаже (его сложнее протягивать по кабельным каналам), чем тонкий. До последнего времени тонкий коаксиальный кабель представлял собой разумный компромисс между основными параметрами линий связи ЛВС и в российских условиях наиболее часто использовался для организации крупных ЛС предприятий и учреждений. Однако более дорогие толстые кабели обеспечивают лучшую передачу данных на большее расстояние и менее чувствительны к электромагнитным помехам.

Витые пары представляют собой два повода, скрученных вместе шестью оборотами на дюйм для обеспечения защиты от электромагнитных помех и согласования импеданса или электрического сопротивления. Другим наименованием, обычно употребляемым для такого провода, является «IBM тип-3». В США такие кабели прокладываются при постройке зданий для обеспечения телефонной связи. Однако использование телефонного провода, особенно когда он уже размещен в здании, может создать большие проблемы. Во-первых, незащищенные витые пары чувствительны к электромагнитным помехам, например электрическим шумам, создаваемым люминесцентными светильниками и движущимися лифтами.


Помехи могут создавать также сигналы, передаваемые по замкнутому контуру в телефонных линиях, проходящих вдоль кабеля локальной сети. Кроме того, витые пары плохого качества могут иметь переменное число витков на дюйм, что искажает расчетное электрическое сопротивление.

Важно также заметить, что телефонные провода не всегда проложены по прямой линии. Кабель, соединяющий два рядом расположенных помещения, может на самом деле обойти половину здания. Недооценка длины кабеля в этом случае может привести к тому, что фактически она превысит максимально допустимую длину.

Защищенные витые пары схожи с незащищенными, за исключением того, что они используют более толстые провода и защищены от внешнего воздействия слоем изолятора. Наиболее распространенный тип такого кабеля, применяемого в локальных сетях, «IBM тип-1» представляет собой защищенный кабель с двумя витыми парами непрерывного провода. В новых зданиях лучшим вариантом может быть кабель «тип-2», так как он включает помимо линии передачи данных четыре незащищенные пары непрерывного провода для передачи телефонных переговоров. Таким образом, «тип-2» позволяет использовать один кабель для передачи как телефонных переговоров, так и данных по локальной сети.

Защита и тщательное соблюдение числа повивов на дюйм делают защищенный кабель с витыми парами надежным альтернативным кабельным соединением. Однако эта надежность приводит к увеличению стоимости.

Волоконно-оптические кабели передают данные в виде световых импульсов по стеклянным «проводам». Большинство систем локальных сетей в настоящее время поддерживает волоконно-оптическое кабельное соединение. Волоконно-оптический кабель обладает существенными преимуществами по сравнению с любыми вариантами медного кабеля. Волоконно-оптические кабели обеспечивают наивысшую скорость передачи; они более надежны, так как не подвержены потерям информационных пакетов из-за электромагнитных помех. Оптический кабель очень тонок и гибок, что делает его транспортировку более удобной по сравнению с более тяжелым медным кабелем.


Однако наиболее важно то, что только оптический кабель имеет достаточную пропускную способность, которая в будущем потребуется для более быстрых сетей.

Пока еще цена волоконно-оптического кабеля значительно выше медного. По сравнению с медным кабелем монтаж оптического кабеля более трудоемок, поскольку концы его должны быть тщательно отполированы и выровнены для обеспечения надежного соединения. Однако ныне происходит переход на оптоволоконные линии, абсолютно неподверженные помехам и находящиеся вне конкуренции по пропускной способности. Стоимость таких линий неуклонно снижается, технологические трудности стыковки оптических волокон успешно преодолеваются.

Беспроводная связь на радиоволнах СВЧ диапазона может использоваться для организации сетей в пределах больших помещений типа ангаров или павильонов, там где использование обычных линий связи затруднено или нецелесообразно. Кроме того, беспроводные линии могут связывать удаленные сегменты локальных сетей на расстояниях 3 - 5 км (с антенной типа волновой канал) и 25 км (с направг ленной параболической антенной) при условии прямой видимости. Организация беспроводной сети существенно дороже, чем обычной.

Для организации учебных ЛС чаще всего используется витая пара, как самая дешевая, поскольку требования к скорости передачи данных и длине линий не являются критическими.

Для связи компьютеров с помощью линий связи ЛС требуются адаптеры сети (или, как их иногда называют, сетевые платы). Самыми известными являются адаптеры следующих трех типов: • ArcNet; • Token Ring; • Ethernet.

Из них последние получили в России подавляющее распространение. Адаптер сети вставляется непосредственно в свободный слот материнской платы персонального компьютера и к нему на задней панели системного блока подстыковывается линия связи ЛС. Адаптер, в зависимости от своего типа, реализует ту или иную стратегию доступа от одного компьютера к другому.

АВТОМАТИЗИРОВАННЫЕ СИСТЕМЫ НАУЧНЫХ ИССЛЕДОВАНИЙ

Автоматизированные системы для научных исследовании (АСНИ) представляют собой программно-аппаратные комплексы, обрабатывающие данные, поступающие от различного рода экспериментальных установок и измерительных приборов, и на основе их анализа облегчающие обнаружение новых эффектов и закономерностей, рис. 6.9.

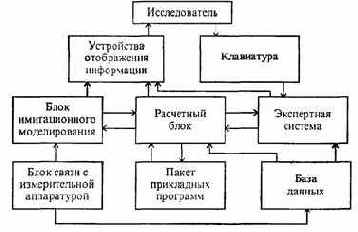
Рис. 6.9. Типовая структура АСНИ

Блок связи с измерительной аппаратурой преобразует к нужному виду информацию, поступающую от измерительной аппаратуры. В базе данных хранится информация, поступившая из блока связи с измерительной аппаратурой, а также заранее введенная с целью обеспечения работоспособности системы. Расчетный блок, выполняя программы из пакета прикладных программ, производит все математические расчеты, в которых может возникнуть потребность в ходе научных исследований Расчеты могут выполняться по требованию самого исследователя, или блока имитационного моделирования. При этом на основе математических моделей воспроизводится процесс, происходящий во внешней среде.

Экспертная система моделирует рассуждения специалистов данной предметной области. С ее помощью исследователь может классифицировать наблюдаемые явления, диагностировать течение исследуемых процессов.

АСНИ получили широкое распространение в молекулярной химии, минералогии, биохимии, физике элементарных частиц и многих других науках.

АВТОМАТИЗИРОВАННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ

Во второй половине 60-х и в 70-х годах получили развитие, так называемые, автоматизированные системы управления сложными объектами хозяйственной деятельности (предприятиями, энергосистемами, отраслями, сложными участками производства).

Автоматизированная система управления (АСУ) - это комплекс технических и. программных средств, совместно с организационными структурами (отдельными людьми или коллективом), обеспечивающий управление объектом (комплексом) в производственной, научной или общественной среде.

Цель разработки и внедрения АСУ - улучшение качества управления системами различных видов, которое достигается

• своевременным предоставлением с помощью АСУ полной и достоверной информации управленческому персоналу для принятия решений;

• применением математических методов и моделей для принятия оптимальных решений.

Кроме того, внедрение АСУ обычно приводит к совершенствованию организационных структур и методов управления, более гибкой регламентации документооборота и процедур управления, упорядочению использования и создания нормативов, совершенствованию организации производства. АСУ различают по выполняемым функциям и возможностям информационного сервиса.

АСУ подразделяют по функциям:

• административно-организационные (например системы управления предприятием —АСУП), отраслевые системы управления - ОАСУ);

•технологические (автоматизированные системы управления технологическими процессами - АСУТП, в свою очередь подразделяющиеся на гибкие производственные системы - ГПС, системы контроля качества продукции - АСК, системы управления станками и линиями с числовым программным управлением);

• интегрированные, объединяющие функции перечисленных АСУ в различных комбинациях.

По возможностям информационного сервиса различают информационные АСУ, информационно-советующие, управляющие, самонастраивающнеся и самообучающиеся.

Первоначально АСУ строились на основе больших ЭВМ, имевшихся в вычислительных центрах крупных предприятий и организаций, и предполагали централизованную обработку информации.
Помимо штата вычислительного центра обслуживание АСУ требовало создания специального подразделения численностью 200 -300 человек.

С появлением персональных компьютеров (ПК) и локальных вычислительных сетей (ЛВС) основой программно-аппаратного обеспечения АСУ стали распределенные информационные системы в сети ПК с архитектурой клиент - сервер. Такие системы позволяют вести учет событий и документальных форм по месту их возникновения, полностью автоматизировать передачу информации лицам, ответственным за принятие решений, создавая, таким образом, предпосылки для перехода к безбумажным комплексным технологиям управления, охватывающим все участки и подразделения предприятий и учреждений, весь производственный цикл.

Остановимся подробнее на структуре и функциях АСУП - наиболее распространенной и одновременно наиболее сложной разновидности АСУ. Управление производством - сложный процесс, требующий согласованной деятельности конструкторов, технологов, производственников, экономистов, специалистов по снабжению и сбыту.

В задачи управления входят

• разработка новых изделий;

• определение технологий изготовления изделий, проектирование оснастки;

• расчет пропускной способности оборудования, потребностей во всех видах ресурсов и производственной программы (плана);

• учет процесса производства, контроль за расходом комплектующих, сырья, ресурсов;

• расчет издержек производства и основных технико-экономических показателей (прибыли, рентабельности, себестоимости и др.).

Многие задачи, с которыми приходится сталкиваться АСУП, оказываются не поддающимися четкой формулировке, их решение основывается на неформальных факторах (например, социально-психологический климат, стиль руководства).

Цели внедрения любой АСУП:

• повышение эффективности принимаемых решений, особенно в части наилучшего использования всех видов ресурсов и сокращения потерь, достигаемых за счет обеспечения процесса принятия решений своевременной, полной и точной информацией, а также применения математических методов оптимизации;



• повышение производительности труда инженерно-технического и управленческого персонала ( и его сокращение) за счет выполнения основного объема учетных и расчетных задач на ЭВМ.

Независимо от профиля АСУП они обладают однотипной функциональной структурой, рис. 6.8.

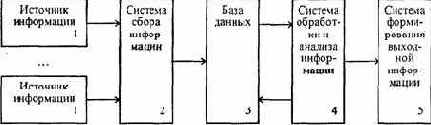
Рис. 6.8. Функциональная структура АСУП

Блок 1 - источники информации. В их роли могут выступать учетчики на различных участках производства, снабжения и сбыта, датчики на рабочих местах. Среди источников информации могут быть и внешние, такие как заказы на поставку продукции, нормативные акты, информация о ценах и другая документация.

Блок 2 выполняет предварительную обработку данных (проверку и уточнение), а затем передает ее в базу данных (блок 3) или непосредственно для последующей обработки и анализа(блок 4).

Блок 3 - база или банк данных. Данные являются результатом сбора информации, измерений характеристик объектов и процессов управления и в таких системах представляются в соответствии с определенными стандартами, образуя базу данных.

Блок 4 обработки и анализа информации - центральный блок АСУ. Он решает следующие задачи:

• управления базой данных, в том числе обеспечения ее обновления и целостности, защиты от несанкционированного доступа;

• реагирования в непредвиденных и аварийных ситуациях, требующих быстрого решения;

• финансовых и учетно-бухгалтерских расчетов типа учета состояния фондов, финансовых и налоговых операций, расчета прибыли и рентабельности;

• составления календарных и оперативных планов, обеспечения заказов на материалы и комплектующие, контроля за выполнением договоров, управления сбытом готовой продукции;

• оценки и прогнозирования рынка, анализа работы трудового коллектива;

• проектно-технологическнх расчетов.

Важнейшее значение при обработке и анализе информации играют экономико-математические модели.

С точки зрения общей организации управления можно выделить следующие основные группы практически используемых экономико-математических моделей:

а) прогнозирования показателей развития предприятия или объединения;



б) оптимизации производственной программы предприятий или объединений;

в) распределения производственной программы по календарным периодам;

г) оптимизации направлений использования фонда развития предприятия или объединения;

д) оптимизации внутрипроизводственных транспортных потоков;

е) оптимизации использования отдельных видов ресурсов;

ж) оптимизации всякого рода нормативов ведения производственно-хозяйственной деятельности предприятий или объединений (партий деталей, норм запасов, размеров производственных резервов и т.д.);

з) разработки балансов производственно-хозяйственной деятельности.

Прогнозирование показателей развития предприятии или объединении осуществляется на основе пользования, главным образом, методов математической статистики. Последние позволяют ориентировочно определить тенденции изменения в перспективе показателей объема выпуска продукции, ее трудоемкости, величины затрат на производство и т.д. Как правило, для использования подобных методов необходимы статистические сведения о деятельности предприятия или объединения в прошлом.

Для определения тенденций развития производственно-хозяйственной деятельности на относительно близкую перспективу используют всякого рода экстраполяционные методы. Для этих целей на основе статистических сведений за прошедшие периоды рассчитывают соответствующие тенденциям развития того или иного аспекта производственно-хозяйственной деятельности регрессионные показатели, которые впоследствии применяют для оценки вероятных перспективных направлений.

Решение задач оптимизации производственной программы сводится к формированию таких номенклатур и объемов выписка продукции, которые в условиях наличных и выделяемых ресурсов, контрольных показателей потребности рынка и ведения деятельности обеспечивали бы оптимизацию принятого критерия. Для решения задач такого класса широко применяют разнообразные модели, базирующиеся на методах линейного программирования; при этом в качестве исходных данных требуются контрольные показатели по выпуску продукции, величина ресурсов (труда, машинного времени и материалов), а также нормы расхода исходных ресурсов на изготовление единицы продукции.



Распределение производственной программы по календарным периодам выражается в установлении номенклатуры и объема выпуска продукции в определенные месяцы и кварталы года. Основной задачей использования моделей такого класса является обеспечение стабильности производственно-хозяйственной деятельности объединения или предприятия в течение рассматриваемого периода.

Оптимизация направлений использования фонда развития производства характерна для объединений, включающих значительное число предприятий. Решение этой задачи позволяет определить рациональные пути использования фонда развития, обеспечивающие достижение оптимума какого-либо критерия (максимизации выпуска продукции, минимизации затрат на производство или максимизации прибыли и т.д.).

Оптимизация использования отдельных видов ресурсов может осуществляться на самых различных уровнях управления производством. К данному классу задач можно отнести оптимизацию раскроя материалов, образования разнообразных смесей, использования оборудования, распределения работ по линиям и т.д. Наиболее типичным представителем данного класса задач является задача образования смеси из разнообразных исходных компонентов с целью минимизации затрат на производство. Такие задачи имеют место практически во всех отраслях народного хозяйства (от нефтепереработки до производства мороженого).

Разработка балансов производственно-хозяйственной деятельности предприятий или объединений осуществляется на основе использования математического аппарата межотраслевого баланса производства и распределения продукции.

Блок 5 - система формирования выходной информации - обеспечивает подготовку (обычно в печатном виде) различного рода .сводок, справок, форм, технологических карт, чертежей и проектной документации, необходимых на производственных участках.

Автоматизированная система управления предприятием может состоять из следующих подсистем управления:

·         технической подготовки производства (конструкторской и технологической подготовки);



·         технико-экономического планирования;

·         бухгалтерского учета;

·         управления материально-техническим снабжением;

·         оперативного управления основным и вспомогательными производствами;

·         управления сбытом;

·         управления кадрами;

·         управления качеством;

·         управления финансами;

·         нормативного хозяйства и др.

Необходимо отметить, что реализация многих проектов АСУП в 70-е годы в нашей стране и во всем мире закончилась неудачей - эти системы «не прижились», оказались нежизнеспособными. В первую очередь, это вызвано тем, что в их концепции были заложены претензии на слишком высокую степень автоматизации управления, не оставляющую места для человека-руководителя. Кроме того, многие математические модели в АСУП были недостаточно точными и приводили к ошибкам.

БАНК ПЕДАГОГИЧЕСКОЙ ИНФОРМАЦИИ

В качестве примера реально существующего и достаточно широко используемого банка данных рассмотрим банк педагогической информации (БПИ), созданный в Республиканском институте повышения квалификации работников образования под руководством В.И.Журавлева. На основе этого банка в ряде регионов России созданы и успешно функционируют региональные банки педагогической информации.

БПИ предназначен для хранения всех видов информации, циркулирующей в системе образования страны, и удовлетворения информационных потребностей пользователей.

С банком работают лица следующих категорий:

• работники образования, получающие с разными целями информацию из банка (к ним относятся учителя, методисты, работники управленческих структур всех уровней, ученые педагоги, преподаватели вузов, студенты и учащиеся, родители и др.);

• поставщики информации, т.е. авторы учебной, учебно-методической и научно-методической литературы, разработчики нормативно-правовой документации, относящейся к системе образования и т.д.;

•работники информационной системы, функция которых состоит в накоплении информационного фонда вторичных документов - информационных модулей, разработанных в соответствии с концепцией БПИ (информационные (информационно-педагогические) модули готовятся на основе первичных материалов, представленных поставщиками информации; такая работа требует специальной подготовки);

• непосредственные работники информационной службы, ведущие лингвистическую часть информационной системы: администратор банка, эксперты.

В перспективе в нашей стране должна быть создана единая сеть банков педагогической информации, объединяющая как центральный республиканский банк, так и региональные БПИ. В последних наряду с информацией общего назначения сосредоточивается информация регионального характера, отражающая опыт учителей и методистов региона, деятельность региональных учреждений повышения квалификации и местных вузов, связанную с региональной системой образования, региональных органов управления образованием и другую информацию педагогической направленности.
Принципиально важной частью такой сети является такая система обмена данными между различными банками, при которой пользователь любого из них может получать информацию из любого банка и отправлять ее туда.

Содержание и структура банка.

Охарактеризуем содержание БПИ приведя перечень и краткое описание нескольких его разделов.

Учебная литература, авторские курсы.

Вариативность отечественного образования - характерное его свойство, возникшее в последнее десятилетие. Почти по всем дисциплинам есть несколько вариантов изложения, подкрепленных учебниками, сборниками упражнений, тестов и т.д. Учитель не может иметь все эти материалы, да в этом и нет необходимости, так как он обычно работает по одному из вариантов. Однако, время от времени возникает потребность ознакомиться и с другими вариантами, что можно сделать с помощью банка.

Особенно эта проблема актуальна при необходимости ознакомиться с разработками по специальным (авторским) курсам, к которым зачастую практически нет другого доступа.

Методы обучения. В конце XX века в образовании во всем мире активизировались поиски новых форм и методов обучения. Это связано со стремительными переменами в общественном устройстве (и, в частности, с информационной революцией). Ежегодно публикуется множество материалов на эту тему, аккумулируемых в БПИ.

Аспекты педагогической науки.

Новые разделы теории воспитания и описание практических приемов реализации педагогических концепций - важная часть педагогической информации.

Диагностика педагогического профессионализма. Проблемы диагностики успехов обучения были актуальны всегда, но стали еще более актуальными в связи с внедрением государственных образовательных стандартов. Все чаще используются тестовые методики контроля, сравнительно новые для нашей школы; на эту тему постоянно возникают новые материалы.

Зарубежная педагогическая информация. Без знания происходящего в этой сфере в мире невозможно правильно ориентироваться в проблемах образования собственной страны. Прямой доступ к зарубежным материалам для большей части работников отечественной системы образования затруднен по финансовым, языковым, терминологическим и прочим причинам.


Аккумулирование в банке обзорных ( и оригинальных) материалов позволяет существенно продвинуться в решении этой проблемы.

Инновации в образовании.

Многочисленные находки учителей, методистов, работников органов управления часто остаются невостребованными просто из-за невозможности ознакомления с ними широкой педагогической общественности. Даже по отношению к широко известным педагогам-новаторам существуют проблемы доступа к конкретным материалам.

Историко-педагогическое наследие,

как отечественное, так и зарубежное, весьма велико, и соответствующие материалы необходимо иметь в БПИ.

Повышение квалификации работников образования - необходимое условие функционирования системы образования. Наряду с давно действующими в этой сфере институтами повышения квалификации, указанной деятельностью занимаются вузы, коммерческие организации и др. Информация на эту тему в БПИ необходима и поможет сделать правильный выбор.

Опыт управленческой работы

для системы образования не менее важен чем чисто педагогический опыт. Приемы организации управления учебными заведениями, учебно-воспитательным процессом систематизируются в БПИ.

Правовая основа педагогической деятельности важна для каждого участника педагогического процесса - учителя, ученика, родителей, администраторов. В системе образования существует большое количество нормативно-правовых актов, накапливаемых в БПИ.

В БПИ содержатся также сведения о рынке образовательных услуг, неформальных объединениях молодежи и других аспектах деятельности системы образования.

Как и во всяком «электронном» банке информации, является важным вопрос о структурных единицах хранения информации. Основной такой единицей является информационно-педагогический модуль (ИПМ). ИПМ - формализованное отражение информации, обладающее следующими свойствами:

• логической законченностью (изложенная в одном ИПМ информация соответствует одному и только одному типу);

• информативностью (объем и качество информации в ИПМ достаточны для ее использования в науке или практике без обращения к источнику);



• популярностью изложения (язык изложения доступен педагогу-практику);

• краткостью изложения (объем ИПМ не превышает 5 кбайт).

ИПМ записываются в специальных форматах. Структура и форма записи в них выбрана таким образом, чтобы информацию мог формализовать не только специально подготовленный человек, но и сам автор, что оправдано экономически и способствует формированию информационной культуры работников образования. Поскольку оформление содержательной (т.е. основной) части информации требует знаний в достаточно узких предметных подобластях образования, никто лучше автора этого сделать не может; администратор же банка (или методист) могут при необходимости оказать автору помощь в некоторых формальных моментах. В то же время, создание ИПМ по источникам, авторы которых не доступны для прямого общения (например, когда ИПМ создается по статьям в зарубежных журналах), могут осуществлять специалисты банка - референты.

Отметим, что подобная практика существует и в научных реферативных журналах, куда может быть помещен либо реферат статьи, написанный референтом, либо автореферат, написанный автором статьи.

ИПМ представляет собой текстовый файл, состоящий из двух полей: поля поискового образа документа и поля записи данных. Каждое из полей распадается на подполя - элементы данных. Рассмотрим структуру и содержание записи отдельно для каждого поля.

Поле поискового образа документа.

В этом поле записываются элементы данных, необходимые для поиска информации, ее классификации, анализа наличия или отсутствия, экспертизы по различным параметрам, осуществления коммуникаций как внутри системы, так и с другими автоматизированными информационными системами. Поскольку параметры информации в таких системах жестко стандартизированы, а эти стандарты (ГОСТы) недостаточно полно отражают специфику педагогических исследований, то допускается описание элементов данных, не имеющих аналога в ГОСТах; они помечаются символом «звездочка» (*). Элементы данных, запись в которых (или ее часть) может повторяться в других подполях, помечены символом (1).


Максимальная длина записи в элементах данного поля составляет 80 байт (длина строки экрана). В тех случаях, когда элемент данных имеет другое ограничение, оно указано в конце строки в скобках.

Структура записи элементов данных:

1) название рубрикатора (*);

2) указатель десятичной классификации (УДК);

3) название тезауруса (*);

4) информационное поле (*);

5) фасет (*);

6) дескриптор тезауруса (1);

7) дата ввода записи;

8) организация - создатель записи;

9) автор, авторский коллектив (*)(1);

10) основное заглавие (250);

11) место работы автора (страна);

12) место работы автора (область);

13) составитель текста записи (1);

14) редактор текста записи (1);

15) переводчик (1);

16) тип информации (*);

17) ключевые слова (через запятую) (1);

18) вид исходного документа;

19) дополнительные данные об исходном документе;

20) библиографическая ссылка (250)(*)(1).

Для формирования пунктов 1-3 необходимо пользоваться справочниками по УДК, пунктов 18 и 19 - таблицами кодов «вид документа» и «код дополнительных данных», имеющимися в документации к банку.

Поясним использованное выше понятие «фасет». Поскольку информационное поле охватывает очень широкий объем понятий, то используется фасетный метод классификации: термины внутри поля располагаются по фасетам - небольшим параллельным группам. Внутри фасеты - дескрипторы, т.е. еще более мелкое дробление. Все это делается для организации эффективного и удобного для пользователя и для системы поиска информации - по классу, по автору, по региону, по ключевым словам. Детальное описание фасетированного рубрикатора находится в документации банка и частично заведено в оболочку пользователя.

Поле записи данных.

В этом поле записывается содержательная часть информации, заносимой в ИПМ. В случае, если информация распадается на ряд единичных типов информации (т.е. образует информационный комплекс), поле записи данных распадается на отдельные подполя, в каждом из которых записывается отдельный ИПМ со своим названием.


Записи ИПМ в этом случае должны образовывать логическую последовательность в дедуктивном порядке. Например, уместно рассматривать данный учебник как совокупность глав по относительно самостоятельным разделам информатики и при составлении соответствующего ИПМ в общее поле записи данных поместить ИПМ по каждой из глав.

Пример информационно-педагогического

модуля. В качестве прообраза, для которого создается ИПМ, рассматривается данный учебник.

Поле поискового образа.

1 Народное образование. Информатика.

2 681.3

3 Тезаурус ЮНЕСКО-МБП по образованию

4 Обучение

5 Обучение

6 Предметное обучение

708.02.1999

8 Авторский коллектив

9 Авторский коллектив в составе: А.В.Могилев, Н.И.Пак, Е.К.Хеннер

10 Информатика

11 Российская Федерация

12 Воронежская область, Красноярский край, Пермская область

13 Е.К.Хеннер

14 И. П. Сидоров

15

16 Учебник

17 Информатика, теоретические основы информатики, программное обеспечение, языки программирования, архитектура ЭВМ, компьютерные сети, информационные системы, компьютерное моделирование

18 Рукопись

19 Учебное пособие для подготовки бакалавров по профилю «Информатика» и учителей информатики

20 Информатика. / Под ред. Е.К.Хеннера. - М.: Издательский Центр «Академия», 1999

Поле записи данных

«Учебное пособие «Информатика» предназначено для подготовки бакалавров по направлению 540106 «Естествознание», профилю «Информатика», магистров по программе «Информатика в образовании» и учителей информатики (специальность 030100 «Информатика»), а также подготовки по педагогическим специальностям, для которых предусмотрено получение дополнительной квалификации «Учитель информатики». Пособие соответствует государственным стандартам по той части предметных блоков, которая касается информатики и вычислительной техники. В пособие включены материалы по следующим разделам: «Теоретические основы информатики», «Программное обеспечение ЭВМ», «Языки и методы программирования», «Вычислительная техника», «Компьютерные сети и телекоммуникации», «Информационные системы», «Компьютерное моделирование».


Материал, включенный в пособие, может обеспечить пяти -шести семестровый курс информатики, изучаемый в педагогических вузах при профильной подготовке по информатике бакалавров, магистров и специалистов -учителей информатики. Пособие может также быть полезным для студентов различных вузов, обучающихся по специальностям, связанным с информатикой. Кроме того, пособие можно использовать при повышении квалификации и переподготовке учителей».

Поиск информации в банке. Здесь речь пойдет лишь о внешней стороне поиска, т.е. его пользовательском интерфейсе. Скрытые от пользователя механизмы поиска обсуждались в гл. 3 (раздел «сортировка и поиск»).

Работа пользователя с банком начинается с меню, изображенном в верхней строчке рис. 6.1.

Рис. 6.1. Вид меню БПИ в режиме «Просмотр»

В режиме «Пользователь» доступны только два поля меню: «Просмотр» и «Выход». Выбрав пункт меню «Просмотр», получаем подпункты, изображенные на рисунке 6.1. Таким образом, любой материал, имеющийся в банке, можно найти тремя различными путями.

Путь «По атрибутам» открывает наиболее широкие возможности поиска информации, отраженные на рисунке 6.2.



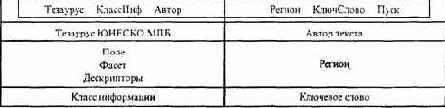
Рис. 6.2. Поиск информации по атрибутам

При поиске по Тезаурусу имеется семь полей, на которые поделено все образовательное пространство:

• вещи (педагогические средства);

• контекст (общество и образование);

• люди (учащиеся и учителя);

• обучение;

• развитие и учение;

• содержание образования и воспитания;

• управление и исследования.

Поиск по фасетам и дескрипторам может происходить: по классу информации, по автору, по региону, по ключевым словам.

Аналогично происходит поиск информации и «По дополнительным реквизитам». При выборе такого пути возникает меню, в котором можно выбирать пункты «Организация», «Составитель», «Редактор», «Дополнительные сведения», «Дата» и продолжать поиск.

Третий путь организации поиска - «По каталогам». Ступив на него, получаем приведенное на рис. 6.3 меню. Выбрав нужный каталог, можем попасть в подкаталоги и т.д., пока не найдем нужного ИПМ или не убедимся в его отсутствии.





Рис. 6.3. Поиск информации по каталогам

Функции администратора банка. Здесь мы опишем лишь те функции администратора банка, которые обусловлены программной оболочкой. Они отражены в следующем меню:



По существу операции означают следующее:

• просмотр и корректировка информационных материалов;

• дополнительный ввод новой информации;

• работа со справочниками (корректировка, доввод);

• создание новой базы с выборкой материалов;

• изменение пароля;

• коррекцию справочников.

После вхождения в пункт меню «Доввод» на экране появляется таблица (рис. 6.4), в которой следует последовательно заполнить позиции; результаты отражаются в колонке «Результаты ввода».

При этом система позволяет воспользоваться рядом встроенных в нее справочников, а также корректировать сами справочники.

Доввод новой информации по позициям заканчивается вводом текста, который должен быть заранее подготовлен в текстовом редакторе (рис. 6.5); при этом необходимо указать диск, на котором находится нужный текст, каталог и название файла.

Данная оболочка позволяет автоматически (раздел меню export) создавать новую базу с выбранными материалами или производить обмен текстами между аналогичными базами. Детальное выполнение этих манипуляций можно произвести следуя указаниям последовательно появляющихся меню.

После описанных выше операций необходимо произвести корректировку базы с помощью операции «Чистка». Эта чисто техническая операция описана в документации.

Для предотвращения недозволенного выполнения пользователями функций по управлению банком операции, доступные лишь администратору, защищены паролем, который следует периодически обновлять.



Рис. 6.4. Операции в меню «Доввод»



Рис. 6.5. Меню для доввода текста

Контрольные вопросы

1. Какие виды информационных систем существуют?

2. Какие типы банков информации различают?

3. Каковы основные компоненты документально-поисковой системы?

4. Что называется индексированием документов? Зачем оно производится?

5. Охарактеризуйте основные типы информационно-поисковых языков.

6. Каково предназначение банков педагогической информации?

7. Какие основные разделы области знаний «Образование» отражены в БПИ?

8. Что представляет собой информационно-педагогический модуль и каков его формат?

9. Какие элементарные данные входят в поле поискового образа?

10. Какие способы поиска информации реализованы в БПИ?

11. Каковы функции администратора БПИ?

БАНКИ ДАННЫХ

Банк данных - наиболее характерный пример информационной системы. В банке данных хранится достаточно универсальная, необходимая для решения разнообразных прикладных задач, информация об определенной предметной области в специальном представлении, чаще всего предполагающем хранение и обработку с помощью компьютеров. При этом сами данные образуют базу данных, а банк, наряду с базой, содержит программные средства обработки данных и реализации запросов, т.е. систему управления базой данных (СУБД). Как правило, банки данных являются системами коллективного пользования. К информации, хранимой в них, часто можно получить доступ по телекоммуникационным сетям.

В современном мире существует огромное число банков данных. В них содержатся сведения коммерческого характера, данные по библиотечным фондам, системам здравоохранения, транспорта и т.д. Быстро развиваются банки, содержащие сведения о системах образования - национальных, региональных (в России они называются «банки педагогической информации»).

Итак, основа банка - база данных. Определение базы данных, основные понятия, связанные с различными моделями данных, уже обсуждались в гл. 2 и это обсуждение будет продолжено ниже в этой главе.

Остановимся на классификации банков информации. Эта классификация может быть проведена с разных точек зрения. По назначению можно выделить следующие классы банков информации:

• информационно-справочные

системы (общего назначения и специализированные);

• банки данных в автоматизированных системах управления (предприятий и организаций, технологическими процессами и т.д.);

• банки данных в системах автоматизации научных исследований.

Однако такая классификация является не вполне строгой и завершенной. По режиму функционирования можно рассматривать банки информации пакетного, диалогового

и смешанного типов, В связи с широким распространением персональных компьютеров, локальных и глобальных сетей ЭВМ подавляющее распространение получили диалоговые системы.

По архитектуре

вычислительной среды различают централизованные

и распределенные банки информации.

К настоящему времени сложились следующие три основных типа банков информации: банки документов, банки данных и банки знаний.

Исторически первым типом банков информации явились банки документов или документальные информационно-поисковые системы. Документальные информационно-поисковые системы бурно развивались в 60-е годы, они широко используются в качестве справочного инструмента пользователей научно-технической информацией, в информационном обслуживании управленческих работников, специалистов и др. В настоящее время интерес к этим системам возобновился в связи с развитием глобальных информационных сетей (Internet) и появлением гипертекстовых серверов типа WWW, Gopher и т.д.. которые вместе с соответствующими поисковыми системами {Archie, Whatis и т.д.) можно отнести к распределенным банкам документов.

Объектом хранения в таких системах является документ (научная статья, монография, приказ, циркуляр, письмо и т.д.) или факты, извлеченные из документов. Для обеспечения поиска и доступа к таким документам необходима их предварительная семантическая обработка - индексация. Индексация до настоящего времени остается неавтоматизированной процедурой и выполняется специалистами -людьми, индексирующими документы и запросы.

БАНКИ ДОКУМЕНТОВ

В документальной информационно-поисковой системе выделяют следующие компоненты:

• массив документов (текстов) или фактов, выступающих в качестве объектов хранения и поиска;

• информационно-поисковый язык, предназначенный для отображения содержания документов и операций над ними, в том числе и запросов для поиска документов;

• правила, алгоритмы, методы индексирования и поиска документов, позволяющие описывать документы и операция над ними на информационно-поисковом языке;

• комплекс программных и аппаратных средств, с помощью которых реализуются процессы накопления, хранения и поиска документов;

• обслуживающий персонал, включающий администратора банка документов, системных аналитиков, программистов и индексаторов. Банки документов работают обычно в двух режимах:

1) избирательного распределения информации, обеспечивающего регулярное текущее информирование пользователей банка о новых поступлениях документов;

2) ретроспективного поиска информации по разовым запросам во всем массиве документов.

Важнейший этап обработки нового документа при поступлении его в хранилище документальной информационно-поисковой системы - индексирование документа -слагается из следующих действий:

1) выявления основного смыслового содержания документа (с учетом точки зрения автора документа и информационных потребностей пользователя системы);

2) описания смыслового содержания документа на информационно-поисковом языке (ИПЯ) и получения соответствующего поискового образа документа (ПОД).

При выполнении ретроспективного поиска производится

1) выявление смыслового содержания запроса;

2) получение поискового обзора запроса (ПОЗ) на информационно-поисковом языке системы.

Результатами индексирования документов и запросов являются их поисковые образы (ПОД и ПОЗ). Поиск документов по запросу означает сопоставление ПОД и ПОЗ. Качество поиска зависит от критериев смыслового соответствия документа запросу (критериев выдачи).

Различают

• теоретико-множественные критерии, основанные на оценке степени совпадения лексических единиц ИПЯ (слов), используемых в ПОД и в ПОЗ;

• критерии, учитывающие с помощью « весовых коэффициентов» относительную информационную значимость отдельных лексических единиц, входящих в ПОЗ;

• логические критерии, основанные на использовании логических операций (дизъюнкции, конъюнкции, импликации и др.).

Информационно-поисковые языки (ИПЯ), которые используются в настоящее время, можно разделить на три большие группы:

• классификационные языки;

•дескрипторные;

• комбинированные.

Языки классификационного типа, в свою очередь, делятся по структуре:

• ИПЯ иерархической структуры;

• ИПЯ фасетной структуры;

• эмпирические (неиерархические) языки.

Классификационные системы.

В иерархических классификационных системах лексические единицы (термины) находятся между собой в отношениях включения. При записи они располагаются в порядке постепенного перехода от общих к более частным. Существуют иерархические системы, в которых рубрики включают по 20 и более подклассов, рубрик и подрубрик в нисходящем порядке. Примером такой иерархической классификационной системы является универсальная десятичная классификация (УДК), широко используемая в библиотечном деле и документальных поисковых системах. УДК охватывает весь спектр знаний.

Шифры УДК, которые можно увидеть на обороте титульного листа всех книг, перед заголовками статей в журналах и сборниках, имеют более чем столетнюю историю. В 1905 г. в Брюсселе на французском языке вышло первое сводное издание таблиц десятичной классификации. Эти таблицы были созданы на основе таблиц десятичной классификации Мельвиля Дьюи, впервые изданных в 1876 г.

Каждый класс (первая ступень деления) в УДК содержит группу более или менее близких наук, например, класс 5 - математику и естественные науки, класс 6 -прикладные науки: технику, в том числе информатику, сельское хозяйство, медицину. Каждая последующая присоединяемая цифра не меняет значения предыдущих, а лишь уточняет их, обозначая более частное понятие. УДК настоящего текста: 681.3:62-52.

В основе фасетной

классификации лежит многоаспектное распределение понятий какой-либо отрасли науки или техники по однородным взаимно исключающим друг друга фасетам.



Примером эмпирической

(неиерархической) классификации может быть алфавитно- предметная классификация. Словарный запас такой классификации состоит из упорядоченного по алфавиту множества слов, словосочетаний и фраз естественного языка, обозначающих предметы какой-либо отрасли науки или практической деятельности. Каждому предмету или вопросу при этом отводится только один индекс, собирающий всю информацию относительно данного предмета или вопроса независимо от аспекта рассмотрения. В предметных классификациях используются следующие термины:

• предметная рубрика (заголовок) - слово или фраза естественного языка, используемая для обозначения основного предмета документа (или запроса);

• предметный подзаголовок - слово или фраза, обозначающая аспект рассмотрения предмета, указанного в предметном заголовке или в подклассе предметов, входящих в класс, обозначенный предметным заголовком;

•предметный словник - упорядоченное по алфавиту множество предметных заголовков, используемых для построения какого-либо каталога или указателя.

Система предметных заголовков и подзаголовков и более мелких разделов создает сложную предметную классификацию по аспектам рассмотрения предмета, т.е. имеет некоторые черты фасетных классификаций.

Дескрипторные информационно-поисковые языки. Дескрипторные информационно-поисковые языки основаны на методе координатного индексирования, сущность которого сводится к тому, что смысловое содержание документа может быть с достаточной точностью и полнотой выражено списком ключевых слов, содержащихся в тексте.

Ключевое слово - это лексическая единица информационно-поискового языка, являющаяся существительным, прилагательным, глаголом, наречием, числительным или местоимением естественного языка или словосочетанием. Основной критерий отбора ключевых слов из текста - степень их полезности для индексирования документа или запроса.

Координатное индексирование выполняется с помощью ключевых слов и логических операции конъюнкции и дизъюнкции. Близкие по смыслу ключевые слова образуют классы условной эквивалентности, имена которых также являются единицами поискового языка и называются дескрипторами.


Дескрипторы вместе с набором ключевых слов языка и семантических связей между ними образуют тезаурус - систематизированный набор данных об области знания, позволяющий в ней ориентироваться.

В дескрипторной статье тезауруса обычно устанавливаются следующие виды семантических отношений:

• отношение синонимии;

• отношение подчинения;

• отношение ассоциации.

Такие связи служат для увеличения полноты представления содержания документов и позволяют формировать запрос не обязательно в ключевых словах документа.

Пример дескрипторной статьи:

языки алгоритмические синонимы: алгоритмические языки

машинно-ориентированные языки проблемно-ориентированные языки вышестоящие: программное обеспечение

языки формальные нижестоящие: автокоды

алгол паскаль фортран си бейсик ассоциации: алгоритмы

программирование

Целесообразность применения того или иного языка во многом зависит от назначения информационной системы, степени ее автоматизации. Для описания документов в библиотеках, общих и технических архивах обычно применяют классификационные языки. В автоматизированных информационно-поисковых системах используются, главным образом, дескрипторные языки.

БАЗОВЫЕ ОПЕРАТОРЫ

Основные базовые операторы (команды) языка Бейсик определяют ввод и вывод данных, присвоение, изменение порядка выполнения команд и циклические конструкции.

INPUT <список объектов ввода>                          - ввод данных;

PRINT < список объектов вывода>                      - вывод данных;

LET a= <арифметическое, логическое

или символьное выражение>

(служебное слово LET можно не писать)            - присвоение;

IF <условие> THEN <оператор1>

ELSE <оператор2>                                                  - условный оператор;

GOTO <номер строки>                                          -безусловный переход;

FOR х= 1 ТО n STEP h <оператор>

NEXTx                                                                      - циклическая конструкция.

Часто используют, так называемый, внутренний ввод данных посредством операторов READ - DATA.

Добавим к этому списку несколько системных команд, с помощью которых программист и пользователь занимаются отладкой и обслуживанием программы:

RUN               - команда запуска программы на выполнение;

LIST               - команда вывода текста программы на экран дисплея;

SAVE                         - команда сохранения текста программы в виде файла;

LOAD            - загрузка ранее сохраненной программы из существующего файла.

Этих операторов и команд обычно хватает, чтобы написать и отладить любую вычислительную программу. Ниже мы познакомимся и с другими командами Бейсика.

Как и во многих языках программирования, в Бейсике имеется набор встроенных функций: математических, логических, символьных и др. Можно сформировать собственные функции с помощью описания DEF, например

DEF FNA(x,y,z)=x*x+y*y+z*z

Рассмотрим пример программы табуляции функции с целью определения ее максимального значения на заданном отрезке. Суть алгоритма заключается в вычислении значений функции Sin(.x) в 100 точках, определенных на задаваемом отрезке [а,Ь] с шагом h=(b-a)/100 и в выборе среди этих значений максимального.

Программа 55

10 REM максимум функции на отрезке

20 INPUT "введите отрезок a,b"; a, b

30 DEF fna (x) = SIN(x)

40 max = fna (a)

50 h = (b - a) / 100

60 FOR x = a TO b STEP h

70 IF max < fna(x) THEN max = fna(x)

80 NEXT x

85 CLS

90 PRINT "максимальное значение функции на отрезке ["; а;

","; Ь; "]="; max

100 END

Здесь в строке 10 - неисполнимый комментарий (который можно организовать и иначе - см. первые строки последующих программ), в строке 85 - команда очистки экрана, в строке 100 - команда «конец программы» (которую часто можно не писать без каких-либо видимых последствий).

Приведем примеры еще нескольких программ на Бейсике, являющихся аналогами программ из §3.

В следующем примере развилка организована с помощью сочетания операторов IF...THEN и GOTO. В современных версиях Бейсика есть конструкция IF...THEN...ELSE; при ее использовании программа 56 станет еще больше похожей на программу 1 (sqr(x) - корень квадратный).

Программа 56 (см. программу 1)

10 REM Квадратное уравнение

20 CLS

30 INPUT "введите коэффициенты А,В,С"; а, Ь, с

40 d = Ъ*Ь -

4*а*с

50 IF d < 0 THEN GOTO 80

60 xl = (-b + sqr(d)) / (2 * a): x2 =

(-b - sqr(d)) / (2 * ay

70 PRINT "корни уравнения xl="; xl; "x2="; х2

80 GOTO 100

90 PRINT "корней нет"

100 END

В следующем примере цикл (с предусловием) организован с помощью операторов IF...THEN и GOTO.

Программа 57 (см. программу 5).

10 REM Машины, прибывающие на склад

20 CLS

30 num = 0: sum = О

40 IF sum >= 100 THEN GOTO 110

50 INPUT "Введите вес груза очередной машины"; w

60 sinn = sum + w

70 IF sum >= 100 THEN GOTO 90

80 num = num + 1: GOTO 90

90 PRINT "груз уже не поместится"

100 GOTO

40

110 PRINT "Количество разгруженных машин =", num

120 END

В программе 58 исходная последовательность задается в блоке данных (строка 30), а затем считывается в массив а. Отсутствие в Бейсике логических переменных преодолено с помощью текстовой переменной р.


При выдаче результатов используется форматная печать PRINT USING (для дробных чисел форматы могли бы быть, например, ###.## - выдаст результат типа 345.98, ##.##лллл - выдаст результат типа 34.17Е-02). В 20-й строке оператор DIM резервирует память под массив (аналог паскалевского описания array, но без явного указания типа элементов).

Программа 58 (см. программу 10).

10 REM bubble (пузырек)

20 DIM a(10)

30 DATA 19, 8, 17, 6, 15, 4, 13, 2, 11, 0

40 CLS

50 PRINT

"Исходный массив"

60 FOR i =

1 TO 10 STEP 1

70 READ a(i)

80 PRINT USING "»#»#"; a(i);

90 NEXT i

100 PRINT

110 p$ = "да"

120 FOR i = 10 TO 2 STEP -1

130 IF a(i) >= a(i-l) THEN GOTO 150

140 b = a(i): a(i) = a(i-l): a(i-l) = Ь: р$ = "нет"

150 NEXT i

160 IF p$ = "нет" GOTO 110

170 PRINT

"Упорядоченный массив"

180 FOR i = 1 TO 10

190 PRINT USING "####"; a(i);

200 NEXT i

210 END

БЕЙСИК И ПАСКАЛЬ

Сопоставим эти популярные языки - не в деталях, а в целом. В Бейсике отсутствуют:

• ряд структур данных (множества, записи, перечисляемые и интервальные типы);

• ссылочные типы и динамические переменные (хотя в старших версиях возможно динамическое описание массивов);

• в большинстве версий - процедуры и функции (их слабыми аналогами являются подпрограммы);

• модули (и, следовательно, возможности организации больших внешних библиотек).

По работе с графикой, возможностям обработки строк (текстов) Бейсик не уступает Паскалю, а по возможностям организации диалога, пожалуй, даже превосходит.

Одна из неприятных особенностей Бейсика для тех, кто привык к структурной записи программного кода, состоит в том, что Бейсик провоцирует программиста к неструктурности. Впрочем, это вопрос навыков и привычек. По большому счету, однако, язык, в котором нет настоящих процедур и средств создания внешних библиотек, не может быть языком структурного программирования.

Усложненные версии Бейсика, в которых фигурируют истинные процедуры и другие средства, заимствованные из более мощных языков, производят неоднозначное впечатление, так как теряется одно из главных достоинств языка - простота (лучше уж тогда пользоваться во многих отношениях превосходящим Бейсик языком операционального программирования Фортран-77). При написании же коротких простых программ Бейсик реально не уступает Паскалю (и многие специалисты утверждают, что процедура программирования на Бейсике проще, хотя это спорно). Поскольку современные версии Бейсик-систем используют не интерпретаторы, а компиляторы, эффективность программ не ниже, чем аналогичных на Паскале.

§ БЕЙСИК КАК ЯЗЫК ОПЕРАЦИОНАЛЬНО-ПРОБЛЕМНО-ОРИЕНТИРОВАННОГО ПРОГРАММИРОВАНИЯ

У языка Бейсик (Basic) весьма своеобразная судьба. Будучи созданным для, так называемых, непрофессиональных программистов, многократно раскритикованный почти каждым пишущим о программировании, он живет \же четверть века и продолжает иметь множество пусть не поклонников, но пользователей. В своих старших версиях он давно перестал быть столь «простым» как его принято почему-то представлять. Его возможности чрезвычайно велики, о чем можно судить хотя-бы по названию одной из недавно вышедших книг - «Разработка экспертных систем на языке Бейсик». На нем создают программы самой различной предметной ориентации. По-видимому, Бейсик продолжает лидировать по количеству пользователей, и хотя бы поэтому знакомство с ним необходимо.

В данном учебнике нет регулярного, «по-порядку». изложения Бейсика. Для человека, освоившего Паскаль, приведенного ниже в этом параграфе текста достаточно, чтобы составить себе отчетливое представление о Бейсике. Количество же учебников по нему столь велико, что нет смысла приводить их список - достаточно заглянуть в любой библиотечный каталог.

Даже при беглом знакомстве обращает на себя внимание некоторая «недисциплинированность» Бейсика - с точки зрения программиста, привыкшего к структурному языку семейства Паскаля. Бейсик относится к языкам операциональным, рожденным от вечно живого Фортрана, в которых необязательно (хотя и вполне возможно) организовывать строго упорядоченные программные структуры. Это и большой недостаток (особенно при разработке крупных программных комплексов), но иногда и достоинство - например, при разработке относительно небольшой диалоговой программы с регулярным обращением к внешним устройствам, сканированием клавиатуры и т.п.

Еще одна проблема, систематически возникающая при работе с Бейсиком - обилие версий и фактическое отсутствие базовой версии. Оставив обзор до конца данного параграфа, укажем лишь, что многие команды и функции в разных версиях сильно различаются, а иногда, существуя в одной, вовсе отсутствуют в другой. Это следует иметь в виду, если приведенные ниже примеры будут не просто анализироваться, а выполняться на ЭВМ, или по их аналогии будут разрабатываться собственные программы. Справочник по реально используемой версии в таком случае просто необходим.

Тексты приведенных в качестве примеров программ отлажены в широко распространенной версии языка QuickBasic.

ЧТО ТАКОЕ КОМПЬЮТЕРНЫЙ ВИРУС

Среди огромного разнообразия видов компьютерных программ существует одна их разновидность, заслуживающая особого упоминания. Главное отличие этих программ от всех остальных состоит в том, что они вредны, т.е. предназначены для нанесения ущерба пользователям ЭВМ. Это - компьютерные вирусы.

Компьютерным вирусом называется программа, обычно малая по размеру (от 200 до 5000 байт), которая самостоятельно запускается, многократно копирует свой код, присоединяя его к кодам других программ («размножается») и мешает корректной работе компьютера и/или разрушает хранимую на магнитных дисках информацию (программы и данные).

Существуют вирусы и менее «злокачественные», вызывающие, например, переустановку даты в компьютере, музыкальные (проигрывающие какую-либо мелодию), приводящие к появлению на экране дисплея какого-либо изображения или к искажениям в отображении дисплеем информации, «осыпанию букв» и т.д.

Создание компьютерных вирусов можно квалифицировать с юридической точки зрения как преступление.

Интересны причины, заставляющие квалифицированных программистов создавать компьютерные вирусы, ведь эта работа не оплачивается и не может принести известности. По-видимому, для создателей вирусов это способ самоутверждения, способ доказать свою квалификацию и способности. Созданием компьютерных вирусов занимаются квалифицированные программисты, по тем или иным причинам не нашедшие себе места в полезной деятельности, в разработке прикладных программ, страдающие болезненным самомнением или комплексом неполноценности. Становятся создателями вирусов и те молодые программисты, которые испытывают. трудности в общении с окружающими людьми, не встречают признания со стороны специалистов, которым чужды понятие морали и этики компьютерной сферы деятельности.

Существуют и такие специалисты, которые отдают свои силы и талант делу борьбы с компьютерными вирусами. В России - это известные программисты Д.Лозинский, Д.Мостовой, П.А.Данилов, Н.Безруков и др. Ими исследованы многие компьютерные вирусы, разработаны антивирусные программы, рекомендации по мерам, предотвращающим уничтожение вирусами компьютерной информации и распространение эпидемий компьютерных вирусов.

Главную опасность, по их мнению, представляют не сами по себе компьютерные вирусы, а пользователи компьютеров и компьютерных программ, не подготовленные к встрече с вирусами, ведущие себя неквалифицированно при встрече с симптомами заражения компьютера, легко впадающие в панику, что парализует нормальную работу.

ЧТО ВПЕРЕДИ?

В 90-х годах микроэлектроника подошла к пределу, разрешенному физическими законами. Фантастически высока плотность упаковки компонентов в интегральных схемах и почти предельно велика возможная скорость их работы.

В совершенствовании будущих ЭВМ видны два пути. На физическом уровне это переход к использованию иных физических принципов построения узлов ЭВМ - на основе оптоэлектроники, использующей оптические свойства материалов, на базе которых создаются процессор и оперативная память, и криогенной электроники, использующей сверхпроводящне материалы при очень низких температурах. На уровне совершенствования интеллектуальных способностей машин, отнюдь не всегда определяемых физическими принципами их конструкций, постоянно возникают новые результаты, опирающиеся на принципиально новые подходы к программированию. Уже сегодня ЭВМ выигрывает шахматные партии у чемпиона мира. а ведь совсем недавно это казалось совершенно невозможным. Создание новейших информационных технологий, систем искусственного интеллекта, баз знаний, экспертных систем продолжатся в XXI веке.

Наконец, уже сегодня огромную роль играют сети ЭВМ, позволяющие разделить решение задачи между несколькими компьютерами. В недалеком будущем и сетевые технологии обработки информации станут, по-видимому, доминировать, существенно потеснив персональные компьютеры (точнее говоря, интегрировав их в себя).

В данном параграфе приведены лишь ключевые события, имена и даты в истории развития одного из наиболее замечательных технических средств, созданных человеком. Более подробную информацию можно найти в указанной в конце главы литературе.

ДАННЫЕ И ИХ ОБРАБОТКА

Суть всех алгоритмов (и компьютерных программ) состоит в том, что они описывают преобразование некоторых начальных данных в конечные. Какие-то данные алгоритм (программа) может использовать как промежуточные. Естественно, что представление и организация данных имеет при разработке алгоритма первостепенное значение. Вопрос о том, как должны быть организованы данные, необходимо решать до того, как начинается разработка алгоритма (программы). Ведь прежде, чем выполнить какие-либо операции, надо иметь объекты, к которым они будут применяться, и четко представлять себе структуру объектов, которые будут получены.

Развитие вычислительной техники и программирования сопровождалось эволюцией представлений о роли данных и их организации. Одним из свойств компьютеров является способность хранить огромные объемы информации и обеспечивать легкий доступ к ней. Информация, подлежащая обработке, в некотором смысле представляет абстракцию фрагмента реального мира. Мы говорим о данных как об абстрактном представлении реальности, поскольку некоторые свойства и характеристики реальных объектов при этом игнорируются (как несущественные ддя данной задачи). Например, каждый сотрудник в списке сотрудников некоторого учреждения представлен множеством данных. Это множество может включать идентифицирующие данные (например, фамилию), данные, относящиеся к тому, что сотрудник делает или к тому, что делают для него. Однако маловероятно, что будут включены такие сведения, как цвет глаз или волос, рост и вес.

Решая конкретную задачу, необходимо выбрать множество данных, представляющих реальную ситуацию. Затем надлежит выбрать способ представления этой информации. Представление данных определяется исходя из средств и возможностей, допускаемых компьютером и его программным обеспечением. Однако очень важную роль играют и свойства самих данных, операции, которые должны выполняться над ними. С развитием вычислительной техники и программирования средства и возможности представления данных получили большое развитие и теперь позволяют использовать как простейшие неструктурированные данные, так и данные более сложных типов, полученные с помощью комбинации простейших данных. Такие данные называют структурированными,

поскольку они обладают некоторой организацией. Современные средства программирования позволяют оперировать с множествами, массивами, записями, файлами (очередями).

В более сложных случаях программист может задать динамические структуры данных, память для хранения которых выделяется прямо в процессе выполнения программы. К таким данным относят линейные списки (одно- и двунаправленные), стеки, деревья, графы.

В последние годы получило развитие, так называемое, объектно-ориентированное программирование, в котором в известной мере устранено противостояние . данных и программ. Объект - это некое образование, состоящее не только из данных, но и из процедур их обработки.

Остановимся подробнее на свойствах различных представлений данных или, как | еще говорят, типах данных.

ДЕЛОВАЯ ГРАФИКА

Одним из первых приложений компьютерной графики стало отображение данных экономических расчетов.

Графические представления расчетных и статистических данных удобно представлять в виде схем, диаграмм, гистограмм и графиков. Различают следующие их виды:

гистограмма - группа столбцов, пропорциональных по высоте определенным числовым значениям;

круговая диаграмма

- секторы круга, углы которых пропорциональны элементам данных;

линейный график - отображение исходных величин в виде точек, соединенных отрезками прямых линий;

временная диаграмма

- последовательность операций или процессов определенной длительности (измерение динамических процессов);

структурная схема - представление сложных объектов в виде дерева или графа;

круговая гистограмма -

представление относительных величин объектов, которым на изображении сопоставляются размеры и расположение кругов в прямоугольной системе координат.

Из числа средств прикладного программного обеспечения общего назначения графическое представление данных лучше всего развито в электронных таблицах и в СУБД.

Одним из первых практических применений машинной графики было автоматическое построение графиков функции в различных системах координат. Обычно графики функций строят в декартовых координатах (в прямоугольной системе, рис. 2.20).

Рис. 2.20. Построение на экране графиков функций (в декартовой системе координат)

В общем виде алгоритм построения графика заданной функции у = f(х) на отрезке [а, b] заключается в следующем.

1. Определяем область значений функции, для чего найдем максимальное по модулю значение функции на заданном отрезке [а, b], т = max(abs (f (x)) для всех x из [а, b].

Примем для удобства, что минимальное значение функции на отрезке совпадает с максимальным, но с обратным знаком. Таким образом, область значений функции лежит в интервале [-т, т].

Поиск максимума можно осуществить разными способами, например, табулируя функцию f(x) на отрезке с разбиением на n частей и определяя максимальное значение в массиве чисел Yi =f(xi), где xi = а + i- (b - а) / п, для i = 0,...
п.

2. Задаем координаты окна x0, y0, x1, у1 на графическом дисплее, в котором будем строить график функции.

3. Формулы преобразования координат х, у точек прямоугольника [а, b]•[-т, т] обычной декартовой системы в соответствующие координаты и, v

окна [x0,x1] • [у0,y1] графического экрана можно задать в следующем виде :

и = x0 + (x - а)(х 1 - x0)/(b - а),

v = (y0 + y1) / 2 – f(x) (y1 – y0) / (2m).

Тогда автоматическое построение графика функции на экране дисплея осуществляется путем установки точек (иi, vi),

соответствующих точкам (xi f(xi)), выбранным в декартовой системе. Часто бывает полезно соединять полученные точки отрезками или специальными линиями, что программы могут делать (или не делать) по пожеланию пользователя.

4. Далее можно оформить график, нарисовав оси координат, нанести масштабные сетки, вывести соответствующие обозначения и комментарии. Оси координат на графическом экране в заданном окне легко построить, вычислив экранные координаты начала выбранной декартовой системы {xv,yv):

xv = х0 - а(х1 - x0)/(b - а),

yv=(y0+y1) / 2.

ДИНАМИЧЕСКИЕ ИНФОРМАЦИОННЫЕ СТРУКТУРЫ

Динамические переменные и указатели.

До сих мы рассматривали статические

переменные. Такие переменные автоматически порождаются при входе в тот блок, в котором они описываются, существуют на протяжении работы всего блока и уничтожаются при выходе их этого блока.

Обращение к статическим переменным производится по их именам, а тип определяется их описанием. Вся работа по размещению статических объектов в памяти машины выполняется на этапе трансляции. Однако использование только статических переменных может вызвать трудности при составлении эффективной машинной программы. Во многих случаях заранее неизвестен размер той или иной структуры данных, или структура может изменяться в процессе выполнения программы. Одна из подобных структур - последовательный файл - уже ранее рассматривалась.

В языке Паскаль предусмотрена возможность использования динамических

величин. Для них выделение и очистка памяти происходит не на этапе трансляции, а в ходе выполнения самой программы. Для работы с динамическими величинами в Паскале предусмотрен специальный тип значений - ссылочный. Этот тип не относится ни к простым, ни к составным. Переменные ссылочного типа, или указатели, являются статическими переменными. Значением переменной ссылочного типа является адрес ячейки - места в памяти соответствующей динамической величины, Свое значение ссылочная переменная получает в процессе выполнения программы, в момент появления соответствующей динамической величины.

Переменные ссылочного типа (указатели) вводятся в употребление обычным путем с помощью их описания в разделе переменных, а их тип, указывающий на тип создаваемых в программе соответствующих динамических величин, тоже определяется либо путем задания типа в описании переменных, либо путем указания имени ранее описанного типа.

Значением указателя является адрес ячейки, начиная с которой будет размещена в памяти соответствующая динамическая величина. Задание ссылочного типа выполняется по схеме

type <имя ссылочного типа> = ^

<имя типа динамической величины>

(значок ^ указывает на то, что величина является динамической).

Например:

type

р = ^ integer;

q = ^

record

х:integer;

у: string [20]

end;

Объявлены два ссылочных типа - р и q. Первый - указатель на целочисленные значения, второй - на двухполевую запись.

Связь указателя с динамическим объектом можно изобразить следующим образом:



На этой схеме р - имя указателя; звездочкой изображено значение указателя, а стрелка отражает тот факт, что значением указателя является адрес объекта (ссылка на объект), посредством которого объект и доступен в программе.

В некоторых случаях возникает необходимость в качестве значения указателя принять «пустую» ссылку, которая не связывает с указателем никакого объекта. Такое значение в Паскале задается служебным словом nil и принадлежит любому ссылочному типу. Результаты выполнения оператора p:=nil можно изобразить

следующим образом:



Имея объявленные типы, можно обычным образом описывать переменные этих типов.

Например,

var i: р; zap: q;

Динамические переменные базовых типов можно вводить прямо в разделе «описания переменных»:

var i: ^integer;

Описание указателя еще не резервирует память для значения соответствующего динамического объекта. Так, каждое вышеприведенное описание выделяет в памяти два байта для записи адреса * - значения указателя, но никакой величины типа р или q в памяти не образуется и даже адреса * еще нет.

Для порождения динамического объекта, на который указывает ссылочная переменная i, сложит стандартная процедура new(i), где new - «новый» - имя процедуры, i - имя указателя, я

Процедура new(i) выполняет две функции:

1) резервирует место в памяти для размещения динамического объекта соответствующего типа с именем i;

2) указателю i присваивает адрес динамического объекта i.

Однако, узнать адрес динамической переменной с помощью процедуры writeln(i) нельзя.

Динамические объекты размещаются по типу стека в специальной области памяти — так называемой «куче», свободной от программ и статических переменных.


Как уже было отмечено, символ ^ после имени указателя означает, что речь идет не о значении ссылочной переменной, а о значении того динамического объекта, на который указывает эта ссылочная переменная. Так, если в программе имеется описание переменной

var:^integer

то при выполнении процедуры new(i) порождается динамическая переменная типа integer. Если затем будет выполнен оператор присваивания

i^:= 58

то этой динамической переменной будет присвоено значение 58.

Имя ссылочной переменной с последующим символом ^ называют «переменной с указателем». Именно она синтаксически выполняет роль динамической переменной и может быть использована в любых конструкциях языка, где допустимо использование переменных того типа, что и тип динамической переменной.

Так, ecли j - статическая переменная типа integer, то допустимы операторы присваивания

j:=j+i^2; i^:i^div 3+4; i^sqr(i^) и т.д.

Если ссылочная переменная b указывает на массив

type mas = array[l... 100] of integer, ,

var b:^mas

то в этом случае переменные с указателем могут выглядеть, например, так:

b^[2], b^[k+5].

Если в процессе выполнения программы некоторый динамический объект р^,

созданный в результате выполнения оператора new(p), становится ненужным, то его можно уничтожить (очистить выделенное ему место в памяти) с помощью стандартной процедуры dispose(p). В результате выполнения оператора вида dispose(p) динамический объект, на который указывает ссылочная переменная р, прекращает свое существование, занимаемое им место в памяти становится свободным, а значение указателя р становится неопределенным (но не равным nil).

Если до вызова процедуры dispose(p) имел пустое значение nil, то это приведет к «зависанию» программы.

Если же до вызова этой процедуры указатель р не был определен, то это может привести к выходу из строя операционной системы.

Значение одного указателя можно присвоить другому указателю того же типа. Можно также указатели одинакового типа сравнивать друг с другом, используя отношения «=» или «<>».



Стандартные процедуры new и dispose позволяют динамически порождать программные объекты и уничтожать их, что дает возможность использовать память машины более эффективно.

Связанные списки данных.

Несмотря на богатый набор типов данных в Паскале, н не исчерпывает всего практически необходимого для разработки многих классов программ. В частности, из разнообразных связанных структур данных

в языке стандартизированы массивы и файлы, а кроме них могут потребоваться и схожие с ними, но иные структуры. Для них характерны, в частности, следующие признаки:

а) неопределенное заранее число элементов;

б) необходимость хранения в оперативной памяти.

Средство для реализации таких структур дает аппарат динамических переменных.

Простейшей из обсуждаемых структур является однонаправленный список. Он строится подобно очереди на прием к врачу: пациенты сидят на любых свободных местах, но каждый из них знает, за кем он в очереди (т.е. данные размещаются на свободных местах в памяти, но каждый элемент содержит ссылку на предыдущий или следующий элемент). Поскольку количество пациентов заранее не очевидно, структура является динамической.

Другая подобная структура, с упоминанием о которой мы уже не раз встречались - стек. Его моделью может служить трубка с запаянным концом, в которую вкатывают шарики. При этом реализуется принцип «последним вошел - первым вышел». Возможное количество элементов в стеке не фиксировано.

Остановимся на примере стека и покажем его программную реализацию. Технически при этом следует решить ряд задач, из которых наиболее специфическими являются

а) связывание последующих компонентов стека;

б) смещение ссылок при каждом движении по стеку.

Из-за необходимости хранить не только значение каждого элемента, но и соответствующую ссылку на последующий элемент, каждый из элементов будем хранить в виде двухполевой записи, в которой первое поле - значение элемента, а второе -ссылка на следующий элемент. Схематически эту структуру можно описать следующим образом





(элементу, который пришел первым, ссылаться не на что, о чем свидетельствует «пустая ссылка» nil).

Пусть для конкретности элементы стека - действительные числа, и при последовательном заполнении состояния стека будут

1,75

35,7                 1,75

-6,94               35,7                 1,75

Приведенная ниже программа включает две процедуры: добавления очередной компоненты к стеку и изъятия ее. Программа формирует указанный стек и производит контрольное извлечение из него. Каждое действие снабжено комментарием, который поможет разобраться в программе. Следует обратить особое внимание на организацию смещения ссылок.

Программа 28

program stack; (формирование динамической структуры - стека}

type s^StackComp; StackComp=record

b:real;

p;s;

end;

var a:s; k:real;

procedure Dobavl(k:real); (процедура добавления к стеку числа «к»}

var j : s ;

begin new(j);           (создание новой динамической записи}

j^.b:=k;           (внесение следующей компоненты стека}

j^.p;=a;        (смещение указателя} a:=j (формирование новой записи)

end;

procedure Vzjat(var k:real); (процедура чтения из стека)

var j :s;

begin j:=а;

k:j^b;                        (k-значение последней компоненты}

a:=j^p;                      (перенастройка указателя)

dispose(j)               (ликвидация использованной записи)

end;

begin                                                          (пример записи и чтения)

a:=nil; Dobavl(1.75) ;

Dobavl(35.7);

Dobavl(-6.94);                  (          сформирован стек: -6.94, 35.7, 1.75)

Vzjat(k); writeln(k); (контрольное взятие из стека)

Vzjat(k); writeln(k); (еще одно взятие из стека)

Vzjat(k); writeln(k)                (еще одно взятие из стека)

end.                                                            (результат работы программы: -6.94 35.7 1.75}

ДИНАМИКА ЧИСЛЕННОСТИ ПОПУЛЯЦИЙ ХИЩНИКА И ЖЕРТВЫ

Рассматривая динамику численности популяций хищника и жертвы, экологи прежде всего стремятся понять ее закономерности и разъяснить различия между типами динамик. В простейших моделях хищник и жертва рассматриваются безотносительно влияния на них других видов. Одна из самых первых и простых моделей была предложена, как и модель межвидовой конкуренции, Лоткой и Вольтеррой, и носит их имя.

Модель состоит из двух компонентов: С

- численность популяции хищника и N -численность популяции жертвы.

Предполагается, что в отсутствие хищника популяция жертвы растет экспоненциально. Чем больше численность той и другой популяции, тем чаще происходят встречи. Число встреченных и съеденных жертв будет зависеть от эффективности, с которой хищник находит и ловит жертву. Если обозначить через а'

«эффективность поиска», то скорость поедания жертвы будет равна a'•C•N, и окончательно для численности жертвы

получаем

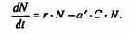
В отсутствие пищи отдельные особи хищника голодают и гибнут. Предположим вновь, что численность хищника в отсутствие пищи будет уменьшаться экспоненциально:

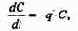
(q - смертность). Скорость рождения новых особей в данной модели полагается зависящей от двух обстоятельств: скорости потребления пищи

a'•C•N, и эффективности f, с которой эта пища переходит в потомство хищника. Итак, для численности хищника окончательно получаем

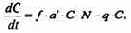
Так как процессы надо рассматривать вместе, объединим уравнения в систему:

(7.68)

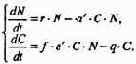
Как и в предыдущем пункте, свойства этой модели можно исследовать, построив изоклины.

Для жертвы имеем

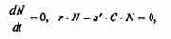
или, выражая С, получаем

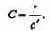
Соответствующее уравнение изоклины для популяции хищника

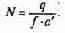
Если поместить обе изоклины на одном рисунке, получим картину взаимодействия популяций (рис. 7.46).

Как видно на рис. 7.47, численности популяций хищника и жертвы совершают периодические колебания: при увеличении численности хищников уменьшается

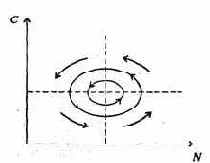
Рис. 7.46. Динамика численности популяции хищника и жертвы. Численность обеих популяций совершает периодические колебания

численность популяции жертвы и наоборот. Такие колебания численности будут продолжаться в соответствии с моделью до тех пор, пока какое-либо внешнее воздействие не изменит численность популяций, после чего произойдет переход в новое устойчивое состояние (такая ситуация называется «нейтральные устойчивые циклы»).

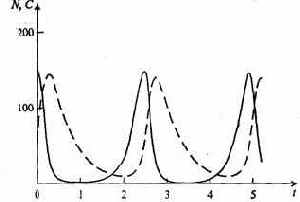
Рис. 7.47. Динамика численности популяции хищника и жертвы при r = 5, а' = 0,1, q = 2,  f = 0,6, N0 = 150, C0 = 50. Сплошная линия - численность жертвы, штриховая – хищника

ДИРЕКТИВЫ ПРЕПРОЦЕССОРА

Препроцессор - это программа, которая производит некоторые, иногда весьма значительные, манипуляции с первоначальным текстом программы перед тем, как он подвергается трансляции.

Оператор препроцессора - это одна строка исходного текста, начинающаяся с символа #, за которым следуют название оператора и операнды.

Операторы препроцессора могут появляться в любом месте программы и их действие распространяется на весь исходный файл.

Весьма часто используют следующие операторы препроцессора:

#include

#define

Более специфичными являются директивы #pragma, #if, #error и др.

Важная возможность препроцессора - включение в исходный текст содержимого других файлов. Эта возможность, в основном, используется для того, чтобы снабжать программы какими-то общими для всех данными, определениями.

Например, чрезвычайно часто в начале программы на языке Си встречается препроцессорная конструкция

#include <stdio.h>

Когда исходный текст программы обрабатывается препроцессором, на место этой инструкции ставится содержимое расположенного в некоем стандартном месте файла stdio.h, содержащего макроопределения и объявления данных, необходимых для работы функций из стандартной библиотеки ввода-вывода. Для использования различных математических функций необходимо подключать файл описаний math.h. Функции, оперирующие со строками, описаны в файле string.h, функции общего назначения - в stdlib.h, функции даты и времени - в time.h, диагностика - в assert, h и т.д.

Директива #define позволяет дать в программе макроопределения (или задать макросы). Оператор макроопределения имеет вид

#define <макроимя> <строка лексем> или

#define <макроимя(<список параметров>)> <строка лексем>

Макроимя - это идентификатор. Строка лексем - это последовательность лексем от Макроимени до конца строки. Точка с запятой в конце макроопределения не ставится.

Препроцессорная обработка макроопределения сводится к тому, что любое появление Макроимени (макровызов) в качестве отдельной лексемы в тексте программы, расположенном после макроопределения, ведет к замене этого Макроимени на указанную Строку лексем.

Например, прочитав определения

#defmePI3.14159

#defineE2.711828

препроцессор заменит в программе все имена PI и Е на соответствующие числовые константы.

Препроцессор языка Си позволяет переопределять не только константы, но и целые программные конструкции. Например, можно написать определение

#define forever for(;;)

и затем всюду писать бесконечные циклы в виде forever

Определение макроимени с параметрами имеет некоторую специфику. Список параметров макроимени - это список идентификаторов, разделенных запятыми. Следующая после списка параметров строка лексем также может содержать эти параметры, которые при макровызове будут заменены на соответствующие аргументы.

Макровызов должен быть отдельной лексемой и состоять из макроимени и заключенного в круглые скобки списка аргументов. При обработке макровызова препроцессор заменяет каждый параметр в строке лексем на соответствующий аргумент макровызова.

В следующих программах иллюстрируются некоторые применения операторов препроцессора.

Пример 1: найти большее из двух чисел.

Программа 110

#include<stdio.h>

#define MAX(X,Y) ((X)>(Y) ? (X) : (Y))

main()

{

int x,y;

scanf ("%d %d", &x, &y); printf ("%d", MAX(x, y) );

)

Результат работы программы:

3                     5

5

Пример 2.

Программа 111

#include<stdio.h>

#define S (x) x*x

#define P(x) printf("x равен

%d.\n",x)

main()

{

int x=4;

int z ;

z = S(x); P(z); z = 3(2);

P(z);

P(S(x));

P(S(x+2));

P(100/S(2));

P(S(++x)) ;

}

Результат работы программы:

x равен 16.

x равен 4.

x равен 16.

x равен 14.

x равен 100.

x равен 30.

Оператор препроцессора #pragma позволяет записывать самые различные указания компилятору (зависящие от конкретного компилятора). Например, следующие два предложения препроцессора

#pragma recursive

#pragma nonrec

устанавливают режим всех функций программы по умолчанию рекурсивным или нерекурсивным. Указание препроцессора

#pragma optimize time

воспринимается компилятором таким образом, что он старается сгенерировать объектный код, отличающийся более высокой скоростью выполнения, чем в случае, когда он должен быть более компактным.

и смена научных картин мира.

1. Абрамов Ю. Ф.

Картина мира и информация (философские очерки). - Иркутск: ИГУ, 1988.

2. Абдеев Р. Ф.

Философия информационной цивилизации. ~ М.: ВЛАДОС, 1994.

3.Аиламазян А. К., Стась Е.В.

Информатика и теория развития. - М.: Наука, 1992.

4. Ахундов М.Д.

Эволюция и смена научных картин мира. В кн.: Философия, естествознание, социальное развитие. - М.: Наука, 1989.

5. Брой М.

Информатика. Основополагающее введение. В 3-х частях. - М.: Диалог-МИФИ, 1996.

6. Будущее искусственного интеллекта. - М.: Наука, 1991.

7. Вейценбаум Дж.

Возможности вычислительных машин и человеческий разум. -М.: Радио и связь, 1982.

8. Венда В. Ф.

Системы гибридного интеллекта: эволюция, психология, информатика. - М.: Машиностроение, 1990.

9. Вирт Н.

Алгоритмы и структуры данных. - М.: Мир, 1989.

10. Вирт Н.

Алгоритмы + структура данных = программы. - М.: Мир, 1985.

11. Глинский Б. А.

Философские и социальные аспекты информатики. - М.: Наука, 1990.

12. Глушков В. М.

Основы безбумажной информатики. /Изд. 2-е. - М.: Наука, 1987.

13. Глушков В. М.

Кибернетика. Вопросы теории и практики. - М.: Наука, 1986.

14. Голицын Г. А., Петров В. М. Информация, поведение, творчество. - М.: Наука, 1991.

15. Гриценко В. И., Паньшин Б.Н. Информационная технология: вопросы развития и применения. - Киев: Наукова Думка, 1988.

16. Громов Г. Р.

Национальные информационные ресурсы. Проблемы промышленной эксплуатации. - М.: Наука, 1985.

17. Громов Г. Р.

Очерки информационной технологии. - М.: Инфоарт, 1992.

18. Дмитриев В. И.

Прикладная теория информации. - М.: Высшая школа, 1989.

19. Интеллектуальные процессы и их моделирование. - М.: Наука, 1987.

20. Информатизация общества и бизнес. - М.: ИНИОН, 1992.

21. Информатика и культура. - М. Наука, 1990.

22. Информационая революция: наука, экономика, технология. Серия «Информация. Наука. Общество». - М.: ИНИОН, 1993.

23. Искусственный интеллект: - В 3-х кн. Кн.З. Программные и аппаратные средства: Справочник / Под ред В.Н.Захарова, В.Ф.Хорошевского. - М.: Радио и связь, 1990.



24. Каныгин Ю. М., Калитич Г. И. Основы теоретической информатики. - Киев: Наукова Думка, 1990.

25. Когнитивная психология и искусственный интеллект. Серия «Информация. Наука. Общество». - М.: ИНИОН, 1993.

26. Лорьер Ж.-Л.

Системы искусственного интеллекта. - М.: Финансы и статистика, 1982.

27. Марков М.

Технология и эффективность социального управления. - М.: Прогресс, 1982.

28. Матросов В.Л.

Теория алгоритмов. - М.: Прометей, 1989.

29. Минский М.

Вычисления и автоматы. - М.: Мир, 1971.

30. Новик И. Б., Абдуллаев Ф.Ш. Введение в информационный мир. - М.: Наука, 1991.

31. Перспективы информатизации общества. Ч.1,2. Серия «Информация. Наука. Общество». - М.: ИНИОН, 1990.

32. Першиков В. И., Савинков В. М. Толковый словарь по информатике. - М.: Финансы и статистика,1991.

33. Попов

Э.П. Экспертные системы: Решение неформализованных задач в диалоге с ЭВМ. - М.: Наука, 1987.

34. Поспелов Г. С.

Искусственный интеллект - основа новой информационной технологии. - М.: Наука, 1988.

35. Рахитов А. И.

Философия компьютерной революции. - М.: ИПЛ, 1991.

36. Свириденко С. С. Современные информационные технологии. - М.: Радио и связь, 1989.

37. Словарь по кибернетике / Под ред. В.С.Михалевича. - Киев: Гл. ред. УСЭ, 1989.

38. Советов Б. Я.

Информационная технология. - М.: Высшая школа, 1992.

39. Становление информатики. Сб. статей из серии «Кибернетика». - М.:, Наука, 1986.

40. Суханов А. П.

Информация и прогресс. - Новосибирск: Наука, 1988.

41. Толковый словарь по искусственному интеллекту / Авторы-составители А-Н.Аверкин, М.Г.Гаазе-Рапопорт, Д.А.Поспелов. - М.: Радио и связь, 1992.

42. УинстонП.

Искусственный интеллект. - М.: Мир, 1980.

43. Урсул А.Д.

Информатизация общества. Введение в социальную информатику. -М.:АОН,1990.

44. Успенский В. А.

Машина Поста. - М.: Наука, 1988

45. Успенский В. А., Семенов А. Л. Террия алгоритмов: основные открытия и приложения. - М.: Наука, 1987.

46. Хартли Р.

Передача информации. В сб. «Теория информации и ее приложения». - М.: ИЛ, 1959.

47. Шеннон К.-Э.

Работы по теории информации и кибернетике. - М.: ИЛ, 1963.

и др. Задачи по программированию.

1. Абрамов С. А.

и др. Задачи по программированию. - М.: Наука, 1988.

2. Абрамов В. Г., Трифонов Н.П., Трифонова Г.Н. Введение в язык Паскаль. - М.:

Наука,1988.

3. Алексеев В.Е.

и др. Вычислительная техника и программирование. Практикум по программированию. - М.: Высшая школа, 1991.

4. Братка И.

Программирование на языке Пролог для искусственного интеллекта.-М: Мир, 1990.

5. Брукс Ф.П.

Как проектируются и создаются программные комплексы. /Очерки по системному программированию/. - М.: Наука, 1979.

6. Буч Г.

Объектно-ориетированное программирование с примерами применения. - Киев: Диалектика, 1992.

7. Ван Тассел Д.

Стиль, разработка, эффективность, отладка и испытание программ.-М.: Мир,1981.

8. Вирт Н. Алгоритмы и структуры данных. - М.: Мир, 1989.

9. Bupт Н. Алгоритмы + структура данных = программы. - М.: Мир, 1985.

10. Герман О. В.

Введение в теорию экспертных систем и обработку знаний. -Минск, Дизайн-ПРО, 1995.

11. Гудман

С, Хидетниеми С. Ведение в разработку и анализ алгоритмов. - М.:

Мир,1981.

12. Дантеманн Д., Мишел Д., Тейлор Д. Программирование в среде Delphy. -Киев: НИПФ-ДиаСофтЛтд., 1995.

13. Дарахавелидзе

П., Марков Е. Delphy - среда визуального программирования. -СПб.: BVH-Санкт-Петербург, 1996.

14. Дайтибегов Д.М., Черноусое Е.А. Основы алгоритмизации и алгоритмические языки. - М.: Финансы и статистика, 1992.

15. ДжонсЖ.,Харроу К. Решение задач в системе Турбо-Паскаль. - М.: Финансы и статистика,1991.

16. Дмитриева М.В., Кубенский А.А. Элементы современного программирования.-С.-Пб.: Изд-во С.-П. университета, 1991.

17. Довгаль

С.И., Литейное Б.Ю., Сбитнев A. Персональные ЭВМ: Турбо-Паскаль V 7.0. Объектное программирование. Локальные сети./Уч. пособие. - Киев:

Информсистема сервис, 1993.

18. Зуев Е.А.

Программирование на языке TURBO PASCAL 6.0 - 7.0. - М.: Радио и связь,1993.

19. Зуев Е.А.

Практическое программирование на языке Турбо-Паскаль о.и, 7.0. -М.: Радио и связь, 1994.

20. Кетков Ю.Л.

Диалог на языке бейсик для мини- и микро-ЭВМ. - М.: Наука, 988.



21. Кнут Д.

Искусство программирования. Т. 1, 2, 3. - М.: Мир, 1976 - 1978.

22. Липаев В. В.

Проектирование программных средств. - М.: Высшая школа, 1990.

23. Ляхович В. Ф.

Руководство к решению задач по основам информатики и вы-- делительной техники. - М.: Высшая школа, 1994.

24. Майерс Г.

Искусство тестирования программ. - М.: Финансы и статистика, 1982.

25. МалпасДж.

Реляционный язык ПРОЛОГ и его применение. - М.: Наука, 1990.

26. Пильщиков В. Н.

Сборник упражнений по языку Паскаль. - М.: Наука, 1989.

27. Поляков Д. Б., Круглое И. Ю. Программирование в среде Турбо-Паскаль. - М.:

А/О Росвузнаука, 1992.

28. Роджерс Д. Ф., Адамс Дж.А. Математические основы машинной графики. -М: Машиностроение, 1980.

29. Рубенкинг И.

Турбо-Паскаль для Windows. Т.1,2. - М.: Мир-СК Ферлаг Ин-тернешнл, 1994.

30. Семакин И. Г.

Лекции по программированию. - Пермь: Изд-во ПГУ, 1996.

31. Сергиевский М. В., Шалашов А. В. Турбо-Паскаль 7.0. - М.: Машиностроение, 1994.

32. Уэйт М., Прата С., Мартин Д. Язык Си. - М.: Мир, 1988.

33. Федоров А., РогаткинД. Borland Pascal в среде Windows. - Киев: Диалектика, 1993.

34. ФоксДж.

Программное обеспечение и его разработка. - М.: Мир, 1985.

35. Хендерсон.

Функциональное программирование.

36. Хьюз Дж., Мичтом Дж. Структурный подход к программированию. - М.:

Мир,1980.

37. Шикин Е. В.

Начала компьютерной графики. - М.: Диалог-МИФИ, 1994.

38. Язык компьютера. SoftWare. Computer languages./Пер. с англ. Под ред. В.М.Курочкина. - М.: Мир, 1989.

Богумирский Б. С. Руководство пользователя

1. Александриди Т.М. и др. Работа на микро-ЭВМ. - М.: Финансы и статистика, 1989.

2. Anoкин И. А., Майстров Л.Е. История вычислительной техники. - М.: Наука, 1980.

3. Богумирский Б. С. Руководство пользователя ПЭВМ. Часть 1. Санкт-Петербург: Печатный Двор, 1994.

4. Брусенцов Н П.

Микрокомпьютеры. - М.: Наука, 1985.

5. Василевский А. М., Кропоткин М.А.. Тихонов В. В, Оптическая электроника. -Л.: Энергоатомиздат, 1993.

6. Васильев Б.М., Частиков А.П Микропроцессоры (история, применение, технология) //Информатика и образование. - 1993. -N 5. -С. 71-83.

7. Гершензон Е. М., Полянина Г. Д., Соина Н. В. Радиотехника. - М.: Просвещение, 1989.

8. Гутер Р. С., Полунов Ю. Л. От абака до компьютера. - М.: Знание, 1975.

9.Джордейн Р.

Справочник программиста персональных компьютеров типа IBM PC, XT и AT. - М.: Финансы и статистика, 1992.

10. Еремин Е.А.

Компилятор? Это очень просто. Компьютер УКНЦ. - М.: Компьютика, 1995.-N3.-С. 25-33.

11. Еремин Е.А., Пономарева Л. В. Методические рекомендации по изучению основных принципов работы ПК. - Пермь: ПГПУ, 1989.

12. Еремин Е.А.

Как работает современный компьютер. - Пермь: из-во ПРИПИТ, 1997.

13. Зальцман Ю.А.

Архитектура и программирование на языке ассемблера БК-0010.//Информатика и образование. 1990.-N4-6: 1991.-N1-5.

14. Крук Б. И., Попов Г.Н. ...И мир загадочный за занавесом цифр... цифровая связь. - М.: Радио и связь, 1992.

15. Лин В.

PDP-11 и VAX-11. Архитектура ЭВМ и программирование на языке ассемблера. - М.: Радио и связь, 1989.

16. Майоров С.А., Кириллов В.В., Приблуда А.А. Введение в микро-ЭВМ. - Л.:

Машиностроение, 1988.

17. Манаев Е.И.

Основы радиоэлектроники. - М.: Радио и связь, 1990.

18. Мнеян М.Г.

Физические принципы работы ЭВМ. - М.: Просвещение, 1987.

19. Нортон П.. Соухэ Д. Язык ассемблера для IBM PC. - М.: Финансы и статистика, 1992.

20. Нортон П.

Персональный компьютер фирмы IBM и операционная система MS DOS. М.: Радио и связь, 1992.

21. Перегудов М.А., Халамайзер А. Я. Бок о бок с компьютером. - М.: Высшая школа,1987.

22. Поляков В. Т.

Посвящение в радиоэлектронику. - М.: Радио и связь, 1990.

23. Смит Б.Э., Джонсон М.Т.

Архитектура и программирование процессора INTEL 80386. - М.: Конкорд. 1992.

24. Токхейм Р.

Основы цифровой электроники. - М.: Мир, 1988.

25. Толковый словарь по вычислительным системам / Под ред. В.Иллингуорта и др. - М.: Машиностроение, 1989.

26. Частиков А. П.

История компьютера. - М.: Журнал «Информатика и образование», 1996.

27. Эндерлайн Р.

Микроэлектроника для всех. - М.: Мир, 1979.

28. Ямпольский В. С. Основы автоматики и электронно-вычислительной техники. -М.: Просвещение, 1991.

Левин В. И. Уравнения математической

1. Араманович И. Г., Левин В. И. Уравнения математической физики. - М.: Наука, 1969.

2. Акулич И. Л.

Математическое программирование в примерах и задачах. - М.: Высшая школа, 1993.

3. Беллман Р.

Математические методы в медицине: Пер. с англ. - М.: Мир, 1987.

4. Белошапка В К

Информационное моделирование в примерах и задачах. -Омск: Из-во ОГПИ, 1992.

5. Бигон М., Харпер Дж., Таунсенд К. Экология. Особи, популяции и сообщества: Пер. с англ. В двух книгах. Кн. 1. - М.: Мир, 1989.

6. Воеводин В. В.

Численные методы алгебры. - М.: Наука, 1966.

7. Гнеденко Б. В.

Курс теории вероятностей. - М.: Наука, 1965.

8. Гнеденко Б. В., Коваленко И. Н. Введение в теорию массового обслуживания. -М.: Наука, 1966.

9. Горстко А. Б.

Познакомьтесь с математическим моделированием. - М.: Знание, 1991.

10. Горстко А. Б., Угольницкий Г. А. Введение в моделирование эколого-зкономических систем. - Ростов: Из-во РГУ, 1990.

11.Гулд X., Тобочник Я. Компьютерное моделирование в физике: Пер. с англ. Т. 1, 2.-М.: Мир, 1990.

12. Демидович Б. П., Марон И. А. Основы вычислительной математики. - М.: Наука,1970.

13. Заварыкин В.М., Житомирский В. Г,. Лапчик М.П. Численные методы. - М.: Просвещение,1990.

14. Зайденберг А. П., Павлович Е.С. Законы распределения случайных величин. -Омск: Изд-во ОГПИ, 1971.

15. Зуховицкий СИ., Авдеева Л. И. Линейное и выпуклое программирование. - М.:

Наука,1967.

16. Кондаков В.М.

Математическое программирование. Элементы линейной алгебры и линейного программирования - Пермь: Из-во ПГУ, 1992.

17. Марчук Г.И.

Математическое моделирование в иммунологии. - М.: Наука, 1991.

18. Математическое моделирование: Пер. с англ. / Под ред. Дж. Эндрюса, Р. Мак-Лоуна. - М.: Мир, 1979.

19. Матюшкин-Герке А. Учебно-прикладные задачи в курсе информатики. Информатика и образование, № 3-4, 5-6, 1992.

20. Мигулин В. В., Медведев В. И., Мустель Е.Р., Парыгин В.Н. Основы теории колебаний. - М.: Наука, 1988.

21. Риклефс Р.

Основы общей экологии: Пер. с англ. - М.: Мир, 1979.

22. Саати Т.

Элементы теории массового обслуживания и ее приложения: Пер. с англ. - М.: Сов. радио, 1971.

23. Сайдашев А. А., Хеннер Е.К. Компьютер на уроке математики. - Пермь: Из-во ПГУ.1991.

24. Самарский А. А., Гулин А.В. Численные методы. - М.: Наука, 1989.

25. Стрелков С П.

Введение в теорию колебаний. - М.: Наука, 1964.

26. Шеннон Р.

Имитационное моделирование систем - искусство и наука: Пер. с англ. - М.: Мир, 1978.

27. Электронные вычислительные машины. / Под ред. АЯ.Соловьева. В 8 книгах. Книга 8. Решение прикладных задач. - М.: Высшая школа, 1987.

ДВИЖЕНИЕ НЕБЕСНЫХ ТЕЛ

Как движется Земля и другие планеты в пространстве? Что ждет комету, залетевшую из глубин космоса в Солнечную систему? Многовековая история поиска ответов на эти и другие вопросы о движении небесных тел хорошо известна; для многих людей, внесших большой вклад в науку, именно интерес к астрономии, устройству большого мира, был первым толчком к познанию.

По закону всемирного тяготения сила притяжения, действующая между двумя телами, пропорциональна их массам и обратно пропорциональна квадрату расстояния между ними. Если поместить начало системы координат на одном из тел (размерами тел по сравнению с расстоянием между ними будем пренебрегать), математическая запись силы, действующей на второе тело, имеет вид (рис. 7.14)

(7.20)

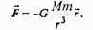
Здесь G = 6,67•10-11 м3/кг•с2) - гравитационная постоянная.

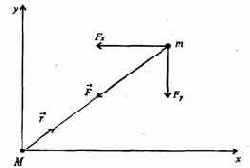
Рис. 7.14. Выбор системы координат при решении задачи двух тел

Знак «минус» в формуле (7.20) связан с тем, что гравитационная сила является силой притяжения, т.е. стремится уменьшить расстояние г между телами.

Далее мы ограничимся лишь изучением взаимного движения двух тел. При этом возникает непростой вопрос: с какой позиции (в какой системе координат) изучать это движение? Если делать это из произвольного положения - например, наблюдатель с Земли изучает взаимное движение Солнца и планеты Юпитер - задача станет для нас слишком сложной. Ограничимся лишь простейшей ситуацией: рассмотрим движение одного из тел с точки зрения наблюдателя, находящегося на втором, т.е., например, движения планеты или кометы относительно Солнца, Луны относительно Земли, пренебрегая при этом относительно небольшими силами притяжения от всех прочих небесных тел. Разумеется, мы тем самым произвели ранжирование факторов, и наши последующие действия имеют отношение к реальности лишь в меру соблюдения определенных условий.

Уравнение, описывающее движение тела m в указанной системе координат, имеет вид

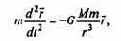
или в проекциях на оси х, у

(7.21)

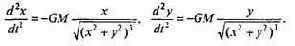
Интересующая нас орбита сильно зависит от «начальной скорости» тела т и «начального расстояния».
Мы взяли эти слова в кавычки, так как при изучении движения космических тел нет столь отчетливо выделенного «начального момента», как в ранее рассмотренных ситуациях. При моделировании нам придется принять некоторое положение условно за начало, а затем изучать движение дальше. Очень часто космические тела движутся практически с постоянной скоростью по орбитам, близким к круговым. Для таких орбит легко найти элементарное соотношение между скоростью и радиусом. В этом случае сила тяготения выступает в роли центростремительной, а центростремительная сила при постоянной скорости выражается известной из начального курса физики формулой mv2/r. Таким образом, имеем

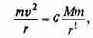
или

(7.22)

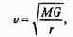
- искомое соотношение.

Период движения по такой орбите



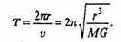
Заметим, что отсюда вытекает один из законов Кеплера, приведший Ньютона к открытию закона всемирного тяготения: отношение кубов радиусов орбит любых двух планет Солнечной системы равно отношению квадратов периодов их обращения вокруг Солнца, т.е. . Более точная формулировка дана ниже (так как реально орбиты планет не вполне круговые). Если соотношение (7.22) нарушено, то орбита не будет круговой. Выяснить, какой она будет, можно в ходе численного моделирования. Сведем (7.21) к системе четырех дифференциальных уравнений первого порядка:

(7.23)

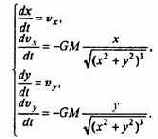
В этой задаче особенно неудобно работать с размерными величинами, измеряемыми миллиардами километров, секунд и т.д. В качестве величин для обезразмеривания удобно принять характерное расстояние от Земли до Солнца ? = 1,496•1011 м, (так называемая, астрономическая единица), период круговой орбиты , соответствующий этому расстоянию, скорость движения по ней , т.е. принять



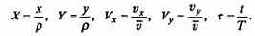
После обезразмеривания получаем

(7.24)

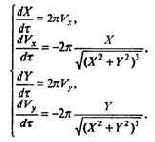
Отметим замечательное обстоятельство: в безразмерных переменных уравнения вообще не содержат параметров! Единственное, что отличает разные режимы движения друг от друга - начальные условия.

Можно доказать, что возможные траектории движения, описываемые уравнениями (7.24) - эллипс, парабола и гипербола.





Рис. 7.15. Иллюстрация второго закона Кеплера

Напомним законы Кеплера, рис. 7.15.

1. Всякая планета движется по эллиптической орбите с общим фокусом, в котором находится Солнце.

2. Каждая планета движется так, что ее радиус-вектор за одинаковые промежутки времени описывает равные площади; на рисунке промежутки времени движения от A1 к A2 и от B1 к B2 считаются одинаковыми, а площади секторов F1A1А2 и F1B1B2 равны. Это означает, что чем ближе планета к Солнцу, тем у нее больше скорость движения по орбите.

3. Отношение кубов больших полуосей орбит двух любых планет Солнечной системы равно отношению квадратов периодов их обращения вокруг Солнца.

Уравнения (7.24) описывают движение не только планет, но и любых тел, попадающих в поле тяготения большой масcы. Так, в Солнечной системе существует огромное количество комет, движущихся по чрезвычайно вытянутым эллиптическим орбитам с периодами от нескольких земных лет до нескольких миллионов земных лет. Судьбы небесных тел, не являющихся постоянными членами Солнечной системы, а залетевших в нее издалека, определяются их скоростью - если она достаточно велика, то орбита будет гиперболической, и. облетев Солнце, тело покинет Солнечную систему, если нет - перейдет на эллиптическую орбиту и станет частью системы; пограничная между ними орбита - параболическая.

Все эти утверждения можно проверить и детально исследовать с помощью уравнений (7.24). При этом полезно и удобно использовать одно важнейшее свойство обсуждаемой системы, которого не было у рассмотренных ранее - сохранение полной энергии движущегося тела (такое свойство называется «консервативность»). Полная энергия движущегося небесного тела т в системе двух тел имеет значение



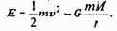
Первое слагаемое - кинетическая, второе - потенциальная энергия. В безразмерных переменных



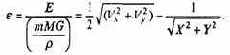
Наличие неизменного параметра е в ситуации, когда изменяются Vx, Vy, X, Y, позволяет контролировать процесс решения системы дифференциальных уравнений, проверять устойчивость метода, подбирать шаг интегрирования.

ДВИЖЕНИЕ ТЕЛА С ПЕРЕМЕННОЙ МАССОЙ: ВЗЛЕТ РАКЕТЫ

Рассмотрим указанную задачу в максимально упрощенной постановке. Наши цели:

а) достичь качественного понимания того, как скорость ракеты меняется во время взлета, как влияют на полет разные факторы;

б) оценить оптимальное соотношение параметров, при котором ракета достигнет первой космической скорости и сможет вывести на орбиту полезный груз.

Таким образом, обсуждаемая модель имеет черты как дескриптивной, так и оптимизационной.

Взлет ракеты - сложный процесс, который неизбежно следует огрубить в попытке получения относительно простых и качественно верных результатов. Например, примем, что сила тяги двигателя - величина постоянная на всем этапе разгона. Реально это, скорее всего, не так. но при упрощенном анализе колебаниями силы тяги пренебрежем, равно как и влиянием случайных порывов ветра и множеством других случайных и неслучайных факторов. Но при таком, даже самом упрощенном, анализе нельзя пренебречь наличием сопротивления воздуха, которое при высоких скоростях очень велико. Ни в коем случае нельзя пренебречь и убыванием массы ракеты в процессе взлета - оно огромно и составляет большую часть исходной массы. Так, у одной из крупнейших отечественных ракет «Энергия» стартовая масса составляет 20000 тонн, а к концу взлета всего 200 тонн.

Поиск математического описания проблем не составляет - в его основе все тот же второй закон Ньютона. Поскольку ракета очень быстро набирает столь высокую скорость, что линейной составляющей силы сопротивления заведомо можно пренебречь, то Fconp = k2v2. Примем, что топливо расходуется равномерно вплоть до его полного выгорания, т.е.

где m0 - начальная масса ракеты, ткон - конечная (т.е. масса полезного груза, выводимого на орбиту), ? - расход топлива; это допущение согласуется с допущением о постоянной силе тяги. Уравнение движения принимает вид в проекции на вертикальную ось

 (7.17)

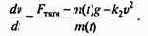
Казалось бы, можно задаться некоторыми значениями величин Fтяги, т0, ?, k2 и проводить моделирование, но это была бы чисто формальная деятельность, не учитывающая еще одного важнейшего обстоятельства.
Поскольку ракета взлетает на огромную высоту (сотни километров), ясно, что сила сопротивления в менее плотных слоях атмосферы не может быть такой же, как вблизи поверхности Земли (при равных скоростях). Действительно, в коэффициент k2

входит величина r -плотность окружающей среды, которая на «космических» высотах во много раз меньше, чем вблизи поверхности. Заглянем в справочник: на высоте 5,5 км плотность воздуха вдвое меньше, чем у поверхности, на высоте 11

км - вчетверо и т.д. Математически зависимость плотности атмосферы от высоты хорошо передается формулой

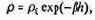
где b = 1,29•10-4

(h измеряется в метрах, ?0 - плотность вблизи поверхности Земли). Поскольку величина h

меняется в ходе полета, уравнение для изменения h(t) следует добавить к уравнению (7.17) и записать следующую систему дифференциальных уравнений:

 (7.18)

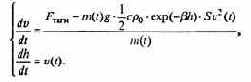
Наша модель становится все более реалистической. Ее совершенствование можно продолжить - например, учесть наличие у ракеты нескольких ступеней, каждая из которых имеет свой запас топлива и тягу двигателя - считая, что после уменьшения массы до некоторого значения сила тяги скачком изменяется; оставим это для самостоятельных размышлений. Перед решением уравнений удобно обезразмерить переменные. Естественной характерной скоростью в данной задаче является первая космическая скорость v* ? 7,8 км/с, при которой возможен вывод на орбиту полезного груза; характерное время - момент полной выработки горючего



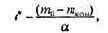
где mкон - масса груза. Реально t* - две-три минуты. За характерную высоту можно взять, например, h* - ту, на которой плотность атмосферы уменьшается в 10 раз (примерно 17 км). Последняя величина может показаться несколько произвольной (впрочем, она таковой и является), но все равно удобнее измерять расстояния в данной задаче относительно величины, равной нескольким километрам, чем в метрах в системе СИ. Итак, введя безразмерные переменные



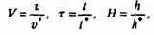
после несложных преобразований получим уравнения



(7.19)

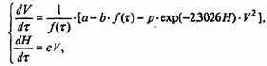
где f(?) - известная функция:



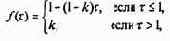
а безразмерные параметры a, b, p, e, k выражаются через исходные так:



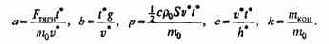
То, что f(?) определяется двумя формулами, связано с наличием двух этапов полета: до и после выработки топлива. Безразмерное время, разделяющее эти этапы - ? = 1; если к этому моменту безразмерная скорость V ? 1, то первая космическая скорость достигнута, в противном случае - нет. Параметр а

управляет режимом полета; если при достижении величиной V значения, равного единице, топливо еще не все выработано (т.е. ? < 1), можно с этого момента либо положить а = 0 («выключить двигатель»), либо продолжать разгон - в зависимости от постановки задачи. Рис. 7.13 иллюстрирует влияние изменения параметра о на динамику взлета ракеты в рамках принятых выше предположений при фиксированных значениях остальных параметров.



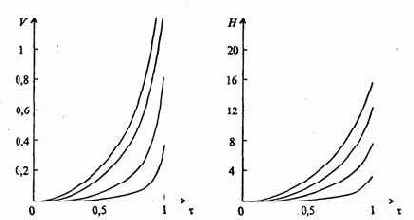
Рис. 7.13. Зависимости V(?) и H(?) при а =

0,2, a = 0,3, a = 0,4 и а = 0,5

 (кривые на рисунках слева направо)

ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ

Закон Кулона, описывающий взаимодействие точечных зарядов, так похож на закон всемирного тяготения, что очевидна близость подходов к моделированию движения заряженной частицы в электростатическом поле и движения малого небесного тела в поле тяжести.

Напомним закон Кулона: между двумя зарядами Q и q разных (одинаковых) знаков действует сила притяжения (отталкивания)

(7.25)

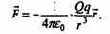
где ?0 = 8,85•10-12

Ф/м - так называемая электрическая постоянная, подробности - в любом курсе физики; Ф/м - «фарада на метр»

Выбор в (7.25) знака «минус» соответствует тому же выбору координат и направлений, что на рис. 7.14, иллюстрирующем закон тяготения.

Первая из задач, которую можно рассмотреть - движение «малого» заряда некоторого знака в поле, создаваемом «большим» неподвижным зарядом другого знака. Эта задача после обезразмеривания уравнений (оставим его читателю) в точности та же, что и рассмотренная выше задача движения «малого» небесного тела. В электростатике, однако, есть возможность рассмотрения широкого круга задач, не имеющих аналога в гравитации. Перечислим простейшие из них:

1) движение «малого» заряда в поле «большого» при взаимном отталкивании;

2) движение заряженного тела в поле, созданном несколькими фиксированными зарядами произвольных знаков (рекомендуем начать со случая, когда все фиксированные заряды лежат в одной плоскости и начальное положение и скорость движущегося заряда - в той же плоскости);

3) движение заряженного тела между пластинами конденсатора (рекомендуем ограничиться плоским движением).

В последнем случае закон Кулона «в лоб» применить трудно - ведь заряженая пластина не может рассматриваться как «точечный заряд». При моделировании можно воспользоваться таким приемом: разбить пластину на несколько маленьких квадратиков, каждому из них приписать приходящийся на его долю заряд и заменить пластину эффективным набором «точечных» зарядов, взаимодействующих с пролетающей частицей. Этот прием - замена непрерывного дробным (дискретизация) обсуждается в следующих разделах.

Моделируя движение заряда, можно получать самые замысловатые траектории, помогающие, с одной стороны, лучше понять закон Кулона, а с другой - научиться визуализации динамических процессов на экране компьютера.

Для решения первой задачи рассмотрим сначала модель, характеризующую движение «малого» заряда в поле «большого», если заряды имеют разные знаки.

Получаем

(7.26)

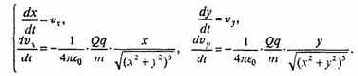
Как обычно, удобно провести обезразмеривание полученной системы. В качестве параметров, с помощью которых проводим обезразмеривание, можно выбрать те, которые характерны для движения «малого» заряда по круговой орбите. Предлагаем читателю самостоятельно проделать эту работу, после чего получаем систему дифференциальных уравнений, практически полностью совпадающую с (7.24), поэтому вновь выписывать здесь ее не будем.



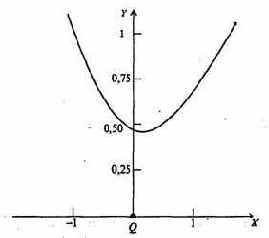
Рис. 7.16. Траектория движения малого положительного заряда

в поле большого положительного заряда при Vx(0) = -2; Vy(0) = -1; X(0) = 1,5; У(0) = 1

Возвращаясь к задаче, когда заряды являются одинаково заряженными и потому отталкиваются, можно заметить, что уравнения будут аналогичными, лишь во втором и в четвертом уравнениях знаки «минус» сменятся на «плюс».

В качестве примера на рис. 7.16 приведена типичная траектория движения при взаимном отталкивании зарядов.

ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ

Особая значимость двоичной системы счисления в информатике определяется тем, что внутреннее представление любой информации в компьютере является двоичным, т.е. описываемым наборами только из двух знаков (0 и 1).

Конкретизируем описанный выше способ в случае перевода чисел из десятичной системы в двоичную. Целая и дробная части переводятся порознь. Для перевода целой части (или просто целого) числа необходимо разделить ее на основание системы счисления и продолжать делить частные от деления до тех пор, пока частное не станет равным 0. Значения получившихся остатков, взятые в обратной последовательности, образуют искомое двоичное число. Например:

                                    Остаток

25 : 2 = 12                                          (1),

12 : 2 = 6                                            (0),

6 : 2 = 3                                              (0),

3 : 2 = 1                                              (1),

1 : 2 = 0                                              (1).

Таким образом

25(10)=11001(2).

Для перевода дробной части (или числа, у которого «0» целых) надо умножить ее на 2. Целая часть произведения будет первой цифрой числа в двоичной системе. Затем, отбрасывая у результата целую часть, вновь умножаем на 2 и т.д. Заметим, что конечная десятичная дробь при этом вполне может стать бесконечной {периодической) двоичной. Например:

0,73 • 2 = 1,46 (целая часть 1),

0,46 • 2 = 0,92 (целая часть 0 ),

0,92 • 2 = 1,84 (целая часть 1),

0,84 • 2 = 1,68 (целая часть 1) и т.д.

В итоге

0,73(10) =0,1011...(2).

Над числами, записанными в любой системе счисления, можно; производить различные арифметические операции. Так, для сложения и умножения двоичных чисел необходимо использовать табл. 1.5.

Таблица 1.5. Таблицы сложения и умножения в двоичной системе

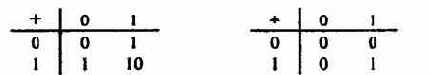
Заметим, что при двоичном сложении 1 + 1 возникает перенос единицы в старший разряд - точь-в-точь как в десятичной арифметике:

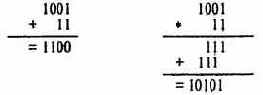
ЕДИНИЦЫ КОЛИЧЕСТВА ИНФОРМАЦИИ: ВЕРОЯТНОСТНЫЙ И ОБЪЕМНЫЙ ПОДХОДЫ

Определить понятие «количество информации» довольно сложно. В решении этой проблемы существуют два основных подхода. Исторически они возникли почти одновременно. В конце 40-х годов XX века один из основоположников кибернетики американский математик Клод Шеннон развил вероятностный подход к измерению количества информации, а работы по созданию ЭВМ привели к «объемному» подходу.

Вероятностный подход

Рассмотрим в качестве примера опыт, связанный с бросанием правильной игральной .кости, имеющей N граней (наиболее распространенным является случай шестигранной кости: N = 6). Результаты данного опыта могут быть следующие: выпадение грани с одним из следующих знаков: 1,2,... N.

Введем в рассмотрение численную величину, измеряющую неопределенность -энтропию (обозначим ее Н). Величины N и Н связаны между собой некоторой функциональной зависимостью:

H = f (N),                                                                  (1.1)

а сама функция f

является возрастающей, неотрицательной и определенной (в рассматриваемом нами примере) для N = 1, 2,... 6.

Рассмотрим процедуру бросания кости более подробно:

1) готовимся бросить кость; исход опыта неизвестен, т.е. имеется некоторая неопределенность; обозначим ее H1;

2) кость брошена; информация об исходе данного опыта получена; обозначим количество этой информации через I;

3) обозначим неопределенность данного опыта после его осуществления через H2. За количество информации, которое получено в ходе осуществления опыта, примем разность неопределенностей «до» и «после» опыта:

I = H1 - H2                                                               (1.2)

Очевидно, что в случае, когда получен конкретный результат, имевшаяся неопределенность снята (Н2

= 0), и, таким образом, количество полученной информации совпадает с первоначальной энтропией. Иначе говоря, неопределенность, заключенная в опыте, совпадает с информацией об исходе этого опыта. Заметим, что значение Н2 могло быть и не равным нулю, например, в случае, когда в ходе опыта следующей выпала грань со значением, большим «З».

Следующим важным моментом является определение вида функции f

в формуле (1.1). Если варьировать число граней N

и число бросаний кости (обозначим эту величину через М), общее число исходов (векторов длины М, состоящих из знаков 1,2,.... N)

будет равно N в степени М:

X=NM.

                                                                      (1.3)

Так, в случае двух бросаний кости с шестью гранями имеем: Х = 62 = 36. Фактически каждый исход Х есть некоторая пара (X1, X2), где X1 и X2 - соответственно исходы первого и второго бросаний (общее число таких пар - X).

Ситуацию с бросанием М

раз кости можно рассматривать как некую сложную систему, состоящую из независимых друг от друга подсистем - «однократных бросаний кости». Энтропия такой системы в М раз больше, чем энтропия одной системы (так называемый «принцип аддитивности энтропии»):

f(6M) = M • f(6)

Данную формулу можно распространить и на случай любого N:

                                                  F(NM) = M • f(N)                                                    (1.4)

Прологарифмируем левую и правую части формулы (1.3): ln X = M • ln N,

М = ln X/1n M.  Подставляем полученное для M значение в формулу (1.4):



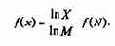
Обозначив через К

положительную константу , получим: f(X) = К • lп Х, или, с учетом (1.1), H=K • ln N. Обычно принимают К = 1 / ln 2. Таким образом

H = log2 N.                                                                (1.5)

Это - формула Хартли.

Важным при введение какой-либо величины является вопрос о том, что принимать за единицу ее измерения. Очевидно, Н будет равно единице при N = 2. Иначе говоря, в качестве единицы принимается количество информации, связанное с проведением опыта, состоящего в получении одного из двух равновероятных исходов (примером такого опыта может служить бросание монеты при котором возможны два исхода: «орел», «решка»). Такая единица количества информации называется «бит».

Все N



исходов рассмотренного выше опыта являются равновероятными и поэтому можно считать, что на «долю» каждого исхода приходится одна N-я часть общей неопределенности опыта: (log2 N)1N. При этом вероятность i-го исхода Рi равняется, очевидно, 1/N.

Таким образом,



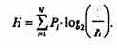
Та же формула (1.6) принимается за меру энтропии в случае, когда вероятности различных исходов опыта неравновероятны (т.е. Рi

могут быть различны). Формула (1.6) называется

формулой Шеннона.

В качестве примера определим количество информации, связанное с появлением каждого символа в сообщениях, записанных на русском языке. Будем считать, что русский алфавит состоит из 33 букв и знака «пробел» для разделения слов. По формуле (1.5)

Н

= log2 34 ? 5 бит.

Однако, в словах русского языка (равно как и в словах других языков) различные буквы встречаются неодинаково часто. Ниже приведена табл. 1.3 вероятностей частоты употребления различных знаков русского алфавита, полученная на основе анализа очень больших по объему текстов.

Воспользуемся для подсчета Н формулой (1.6); Н ? 4,72 бит. Полученное значение Н,

как и можно было предположить, меньше вычисленного ранее. Величина Н, вычисляемая по формуле (1.5), является максимальным количеством информации, которое могло бы приходиться на один знак.

Таблица 1.3. Частотность букв русского языка

i	Символ	Р(i)	i	Символ	P(i)	i	Символ	Р(i)
1	Пробел	0,175	13		0,028	24	Г	0.012
2	0	0,090	14	М	0,026	25	Ч	0,012
3	Е	0,072	15	Д	0,025	26	И	0,010
4	Ё	0,072	16	П	0,023	27	X	0,009
5	А	0,062	17	У	0,021	28	Ж	0,007
6	И	0,062	18	Я	0,018	29	Ю	0,006
7	Т	0,053	19	Ы	0,016	30	Ш	0.006
8	Н	0,053	20	З	0.016	31	Ц	0,004
9	С	0,045	21	Ь	0,014	32	Щ	0,003
10	Р	0,040	22	Ъ	0,014	33	Э	0,003
11	В	0,038	23	Б	0,014	34	Ф	0,002
12	Л	0,035

<


Аналогичные подсчеты Н

можно провести и для других языков, например, использующих латинский алфавит - английского, немецкого, французского и др. (26 различных букв и «пробел»). По формуле (1.5) получим

H = log2 27 ? 4,76 бит.

Как и в случае русского языка, частота появления тех или иных знаков не одинакова.

Если расположить все буквы данных языков в порядке убывания вероятностей, то получим следующие последовательности:

АНГЛИЙСКИЙ ЯЗЫК:                             «пробел», E, T, A, O, N, R, …

НЕМЕЦКИЙ ЯЗЫК:                                  «пробел», Е, N, I, S, Т, R, …

ФРАНЦУЗСКИЙ ЯЗЫК:                           «пробел», Е, S, А, N, I, Т, …

Рассмотрим алфавит, состоящий из двух знаков 0 и 1. Если считать, что со знаками 0 и 1 в двоичном алфавите связаны одинаковые вероятности их появления (Р(0) = Р(1) = 0,5), то количество информации на один знак при двоичном кодировании будет равно

 H = 1оg2 2 = 1 бит.

Таким образом, количество информации (в битах), заключенное в двоичном слове, равно числу двоичных знаков в нем.

Объемный подход

В двоичной системе счисления знаки 0 и 1 будем называть битами (от английского выражения Binary digiTs - двоичные цифры). Отметим, что создатели компьютеров отдают предпочтение именно двоичной системе счисления потому, что в техническом устройстве наиболее просто реализовать два противоположных физических состояния: некоторый физический элемент, имеющий два различных состояния: намагниченность в двух противоположных направлениях; прибор, пропускающий или нет электрический ток; конденсатор, заряженный или незаряженный и т.п. В компьютере бит является наименьшей возможной единицей информации. Объем информации, записанной двоичными знаками в памяти компьютера или на внешнем носителе информации подсчитывается просто по количеству требуемых для такой записи двоичных символов. При этом, в частности, невозможно нецелое число битов (в отличие от вероятностного подхода).

Для удобства использования введены и более крупные, чем бит, единицы количества информации.Так, двоичное слово из восьми знаков содержит один, байт информации, 1024 байта образуют килобайт (кбайт), 1024 килобайта - мегабайт (Мбайт), а 1024 мегабайта - гигабайт (Гбайт).

Между вероятностным и объемным количеством информации соотношение неоднозначное. Далеко не всякий текст, записанный двоичными символами, допускает измерение объема информации в кибернетическом смысле, но заведомо допускает его в объемном. Далее, если некоторое сообщение допускает измеримость количества информации в обоих смыслах, то они не обязательно совпадают, при этом кибернетическое количество информации не может быть больше объемного.

В дальнейшем тексте данного учебника практически всегда количество информации понимается в объемном смысле.

ФИЗИКА И МОДЕЛИРОВАНИЕ

Физика - наука, в которой математическое моделирование является чрезвычайно важным методом исследования. Наряду с традиционным делением физики на экспериментальную и теоретическую сегодня уверенно выделяется третий фундаментальный раздел - вычислительная физика (computational physics). Причину этого в целом можно сформулировать так: при максимальном проникновении в физику математических методов, порой доходящем до фактического сращивания этих наук, реальные возможности решения возникающих математических задач традиционными методами очень ограниченны. Из многих конкретных причин выделим две наиболее часто встречающиеся: нелинейность многих физических процессов (примеры - ниже в тексте) и необходимость исследования совместного движения многих тел, для которого приходится решать системы большого числа уравнений. Часто численное моделирование в физике называют вычислительным экспериментом, поскольку оно имеет много общего с лабораторным экспериментом.

Таблица 7.1

Аналогии между лабораторным и вычислительным экспериментами

Лабораторный эксперимент		Вычислительный эксперимент
Образец Физический прибор Калибровка прибора Измерение . Анализ данных		Модель Программа для компьютера Тестирование программы Расчет Анализ данных

Численное моделирование (как и лабораторные эксперименты) чаще всего является инструментом познания качественных закономерностей природы. Важнейшим его этапом, когда расчеты уже завершены, является осознание результатов, представление их в максимально наглядной и удобной для восприятия форме. Забить числами экран компьютера или получить распечатку тех же чисел не означает закончить моделирование (даже если числа эти верны). Тут на помощь приходит другая замечательная особенность компьютера, дополняющая способность к быстрому счету - возможность визуализации абстракций. Представление результатов в виде графиков, диаграмм, траекторий движения динамических объектов в силу особенностей человеческого восприятия обогащает исследователя качественной информацией. Во многих рассматриваемых ниже физических задачах фундаментальную роль играет второй закон Ньютона - основа всей динамики:

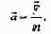
В уточненной редакции закон утверждает: ускорение, с которым движется тело в данный момент времени, пропорционально действующей на него в этот момент силе и обратно пропорционально имеющейся в данный момент у тела массе.

Разные записи этого утверждения:

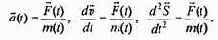
Связывая мгновенные значения величин, второй закон Ньютона позволяет изучать движение тел при произвольных изменениях во времени силы и массы.

ФОРМАТЫ ДАННЫХ

Почти каждая команда процессора нацелена на обработку данных, местонахождение которых определяется значениями адресов операндов. Для понимания работы процессора существенно представлять, какого рода данные он может обрабатывать.

Если в ходе исполнения программы ее остановить, прочитать содержимое какой-нибудь ячейки памяти ОЗУ, к которой в это мгновение обращается процессор, и попытаться понять, что именно хранится в этой ячейке, то это чаще всего невозможно сделать, не расшифровав код выполняемой операции - сам по себе хранимый в ячейке двоичный код может быть и числом, и командой, и кодом символа, и чем-то еще. Все дело в том, как его интерпретирует работающая с ним команда.

Перечислим некоторые форматы данных, типичные для 16- разрядной ЭВМ.

8- битовые целые числа без знака. Каждое такое число занимает 1 байт и воспринимается процессором как целое положительное число. Следовательно, диапазон представимости чисел в этом формате от 00000000 до 11111111, т.е. от 0 до FF в шестнадцатеричной системе (от 0 до 255 в десятичной).

8- битовые целые числа со знаком. В этом случае величина числа задается семью битами, а значение старшего бита определяет знак числа (0 - положительное, 1 -отрицательное). Например, в этом формате код 01101011 означает число +6В.

Однако код 11101011 не означает, как можно подумать, число -6В, так как для кодирования отрицательных чисел применяется, так называемый, дополнительный код. Он образуется следующим образом:

• находится восьмиразрядное двоичное представление абсолютной величины числа;

• найденный код инвертируется, т.е. в нем нули заменяются на единицы и наоборот;

• к полученному коду арифметически прибавляется единица.

Например, процесс получения дополнительного кода десятичного числа -75 таков:

01001011      10110100      10110101

/

Использование дополнительного кода облегчает организацию арифметических действий в процессоре (который, как правило, не имеет даже аппаратно реализованной операции вычитания - все удается свести к сложению целых чисел).

Обратная процедура - восстановление значения числа по дополнительному коду - осуществляется по тому же правилу, что и прямая.

Диапазон представимости чисел в этом формате: от-128 до +127.

16- битовые целые числа со знаком и без знака. Они в точности аналогичны 8-битовым, но код имеет вдвое большую длину. Соответственно, многократно возрастает диапазон представимости: для чисел без знака от 0000 до FFFF (т.е. от О до 65535 в десятичной системе), для чисел со знаком - от -8000 до +7FFF (т.е. в десятичной системе от -32768 до +32767).

8- битовые символы.

В этом формате двоичный код интерпретируется обрабатывающей его командой как код символа. При работе с персональными ЭВМ обычно используется система кодирования ASCII, о которой говорилось в главе 1. В этой системе стандартизированы (закреплены за определенными символами) коды, у которых значение старшего бита равно 0; все прочие коды остаются за символами национальных алфавитов и дополнительными специальными символами.

Битовые поля.

В этом формате значащим является не весь 8- или 16- разрядный код в целом, а каждый из составляющих его битов. Один из примеров битового поля - содержимое регистра состояния процессора (см. выше). Другой пример -форма хранения множеств в языке «Паскаль».

Существуют и другие форматы данных - двоично-десятичные числа, строки и т.д.

ФОРМЫ. УПРАВЛЯЮЩИЕ КОНСТРУКЦИИ В ЛИСП-ПРОГРАММЕ

Программа состоит не только из функций, но и из форм. Простейшими формами являются константы, переменные, лямбда-вызовы, вызовы функций.

Остановимся более подробно на специальных формах, предназначенных для управления обработкой программы и контекстом. У каждой формы определенный синтаксис и семантика, основанные на едином способе записи и интерпретации.

Управляющие предложения Лиспа внешне выглядят как вызовы функций - в виде скобочных выражений, первый элемент которых действует как имя управляющей структуры, а остальные элементы - как аргументы. Наиболее важные формы можно разделить на следующие группы:

работа с контекстом

• QUOTE или блокировка вычисления,

• вызов функции и лямбда-вызов,

• предложения LET и LET*;      

последовательное исполнение

• предложения PROG1, PROG2 и PROGN;

разветвление исполнения

• условные предложения COND, IF, WHEN, UNLESS,

• выбирающее предложение CASE;

итерации

• циклические предложения DO, DO*, LOOP, DOTIMES, DOUNTIL;

передачи управления

• предложения PROG, GO и RETURN;

динамическое управление вычислением

• THROW, CATCH, а также BLOCK.

Эти управляющие формы (кроме QUOTE и лямбда-вызова, а также вызовов функций), в основном, используются в теле лямбда-выражений, определяющих функции.

Предложение LET используется для создания связи переменных внутри формы:

(LET ((пep1 знач1) (пер2 знач2)...) форма1 форма2 ...).

При вычислении этого выражения статические переменные пep1, пер2, ... связываются (одновременно) с соответствующими значениями знач1, знач2, ..., а затем вычисляются значения форм форма1, форма2, ... Значение последней формы возвращается как общий результат. Форма LET* отличается от LET лишь тем, что связывание переменных и вычисление форм происходит не одновременно, а последовательно, вначале 1-е, потом 2-е и т.д.

Например:

(let*((x2)(y(*3x)))

(list x у)

Результат: (2 6).

Предложения PROG1, PROG2 и PROGN позволяют организовывать последовательные вычисления из нескольких вычисляемых форм:

(PROG1 форма1 форма2 ... формаn)

(PROG2 форма1 форма2 .. формаn)

(PROGN форма1 форма2 . формаn).

Различие этих форм лишь в возвращаемых ими в качестве общего значения результатах. Форма PROG1 возвращает значение формы1, PROG2-формы2, PROGN -последней формы n.

Например:

(progn (setq x 2) (setq у (* 3 х)))

Результат: 6.

Предложение COND является основным средством разветвления обработки. Структура условного предложения такова:

(COND (р1 а1) (р2 а2)... (pn an)).

pi - это предикаты (выражения-условия, которые могут быть либо истинными (Т), либо ложными (NIL)). Их значения вычисляются слева направо, пока не будет получено значение «истина» (Т), затем вычисляется и возвращается в качестве результата результирующее выражение ai. соответствующее 1-му истинному предикату pi. Если истинного предиката нет. то значение COND - NIL. Форма ai для соответствующего предиката может отсутствовать (тогда возвращается значение этого предиката в случае его истинности), или, наоборот, может быть задана последовательность форм для предиката pi - тогда эти формы вычисляются последовательно и возвращается значение последней.

В следующем примере с помощью предложения COND определена функция, устанавливающая тип выражения:

(defun тип (1)

(cond ((null 1) 'пусто)

((atom 1) 'атом)

(t 'список)))

Результат: ТИП.

Примеры применения этой функции:

(тип ' (a b с))

Результат: СПИСОК.

(тип (atom ' (а т о м)))

Результат: ПУСТО.

Для организации ветвления можно использовать и  формулы IF, WHEN, UNLESS:

(IF условие то-форма иначе-форма),

что эквивалентно

(COND (условие то-форма) (Т иначе форма));

(WHEN условие форма1 форма2 ...),

что эквивалентно

(UNLESS (NOT условие) форма! форма2 ...)

или

(COND (условие форма1 форма2 ...)).

Можно применять и выбирающее предложение CASE:

(CASE ключ (список ключей1 форма11 форма12 ...)

(список ключей2 форма21 форма22 . . .)

В этой форме сначала вычисляется значение ключевой формы «ключ», затем происходит сравнение с элементами списков ключей и, если найдено значение ключевой формы, вычисляется последовательность соответствующих форм, значение последней из которых возвращается как значение всего выражения CASE.

Предложения PROG, GO и RETURN аналогичны конструкциям неструктурных языков программирования (типа FORTRAN, Бейсик); пользоваться ими не рекомендуется.

ФУНКЦИИ

Функции в Лиспе аналогично математическим функциям ставят в соответствие элементам из одного множества - определения (аргументов) - единственный элемент из множества значений. В программах следует различать определение функций и вызов (применение) функции.

В языке Лисп принята единообразная префиксная форма записи, при которой как имя функции или действия, так и аргументы записываются внутри скобок:

(f x)

(g x y) (сумма_квадратов 2 3).

Аналогично записываются и арифметические действия:

(+ х у)

(*x(+yz))

(+ (^ х х) (+ у у)).

Определение функций и их вычисление в Лиспе основано на лямбда-исчислении Черча. В 1-исчислении Черча функция записывается в виде

1(х1,х2,... ,xn) .fn

В Лиспе 1-выражение имеет вид (LAMBDA (xl, x2,..., xn).fn).

Символ LAMBDA означает, что мы имеем дело с определением функции. Символы xi являются формальными параметрами, они образуют список, называемый лямбда-списком; fn - это тело функции, которая может иметь произвольную форму, допускаемую интерпретатором Лиспа. Телом функции может быть, например, константа или композиция из вызовов функций. Функцию, вычисляющую сумму квадратов двух чисел, можно, например, определить так:

(lambda(xy)(+(*xx)(*yy))).

Лямбда-выражение - это безымянная функция, которая может быть использована для связывания формальных и фактических параметров на время вычислений. Вызов такой функции происходит по форме

(лямбда-выражение а1 а2 ... an)

Здесь ai - фактические параметры, с которыми происходит вычисление.

Например

((lambda (х у) (+ (* х х) (* у у))) 3 4).

Результат: 25.

Определить новую функцию и дать ей имя для последующих вызовов можно с помощью функции DEFUN (define function):

(DEFUN имя лямбда-список тело).

DEFUN соединяет символ с лямбда-выражением, и символ начинает представлять (именовать) определенные этим лямбда-выражением вычисления. Значением этой формы является имя новой функции:

(defun sumsquare (х у) (+ (* х х) (* у у))) .

Результат: sumsquare.

Вызов (применение) этой функции:

(sumsquare 34)

Результат: 25.

Определение функции задается списком, поэтому его можно модифицировать в ходе выполнения программы. Кроме того, некоторый символ может быть и именем функции и переменной.

В Лиспе передача параметров происходит по значению. Формальные параметры функций являются статическими и локальными, т.е. действительны только внутри той формы, в которой они определены.

Основу для построения различных функций образует набор небольшого числа примитивных встроенных функций. Базовыми функциями обработки S-выражений являются функции

CAR, CDR, CONS, ATOM, EQ, EQL, =

и другие, смысл которых отражен в табл. 3.7.

Таблица 3.7

Базовые функции обработки S-выражений

Функция	Вызов	Действие	Пример использования
CAR	(CAR список)	Возвращает головною часть	(CAR(1 234))
		списка - его 1-й элемент	Результат:1
CDR	(CDR список)	Возвращает хвостовую часть	(CDR(! 234))
		списка- все. кроме 1-го элемента	Результат:(2 3 4)
CONS	(CONS S-выра-	Строит список из переданных в	(CONS I (2 3 4))
	жение список)	качестве аргументов головы и хвоста	Результат: (1234)
ATOM	(ATOMS-выра-	Предикат; проверяет, является ли	(ATOM A) : t
	жение)	аргумент атомом, и возвращает либо t	(ATOM (1 2 3)): Nil
		(истина), либо Nil или ("(ложь)
EQ	(EQ символ	Предикат: проверяет тождественность	(EQ A A): t
	символ)	символов-аргументов, неприменим	(EQ X (CAR (X Y Z))): t
		для чисел
EQL	(EQL число	Предикат, проверяет тождественность	(EQL 3.0 3.0): t
	число)	чисел одного типа
=	(= число	Предикат, проверяет тождественность
	число)	чисел различных типов	(=30.3el):t
EQUAL	(EQUAL число	Аналогична EQL,	(EQUAL(xyz)(xyz)):t
	или список	но, кроме того, проверяет идентичность
	число или список)	Списков
EQUALP	(EQUALP	Проверка наиболее общего равенства
	объект объект)
NULL	(NULL список)	Проверка, является ли аргумент
		пустым списком
NOT	(NOT логическая	Логическое отрицание
	величина)
NTH	(NTH n список)	Выделение n-го элемента списка	(NTH 2 (1 2 3)): 3
			(индексы начинаются с 0)
FIRST		Предикаты, выделяющие
SECOND		Соответствующие элементы списка
LAST
LIST	(LIST apr	Строит из аргументов список	(LIST a b (с)): (a b c)
	арг2 ...)

<


Отметим, что в программах на Лиспе надо тщательно отличать значения от их обозначений.

В Лиспе константы обозначают самих себя. Выражения типа (* 2 2) сразу вычисляются. Чтобы избежать нежелательного вычисления выражения используется функция QUOTE или знак апострофа (') перед выражением:

(* 2 2) : 4

' (* 2 2) :' (* 2 2) – список

Произвольный символ можно использовать как переменную, и он может обозначать произвольное выражение. При первом использовании символу должно быть присвоено или с ним связано некоторое значение с помощью функции SET, например,

(SET 'операции' (+ - * /))

Знак ' используется для подавления вычисления аргументов функции SET. Функция SETQ не вычисляет значения 1-го аргумента (а 2-го вычисляет).

На значение символа можно сослаться, указав его без апострофа (').

Для занесения значений в ячейку памяти, связанной с символом, можно пользоваться обобщенной функцией присваивания SETF, размещающей значения в соответствующей ячейке памяти:

(SETF ячейка_памяти значение).

Переменная «ячейка_памяти» без апострофа указывает на ячейку памяти. Присвоение, выполняемое функциям» SET, SETQ и SETF, является побочным эффектом , этих функций, помимо того, данные функции возвращают присваиваемые значения.

ФУНКЦИИ ЧЕЛОВЕКА И МАШИНЫ В СИСТЕМАХ УПРАВЛЕНИЯ

Хорошо изученной сферой применения кибернетических методов является технологическая и производственная сфера, управление промышленным предприятием. Задачи, возникающие в управлении предприятием среднего и большого масштаба, уже весьма сложны, но допускают решение с использованием электронно-вычислительных машин. Системы управления хозяйством предприятий или территорий (регионов, городов), использующие ЭВМ для переработки и хранения информации, получили название автоматизированных систем управления (АСУ). По своему характеру такие системы являются человеко-машинными, т.е. наряду с использованием мощных компьютеров предполагающими наличие в них человека с его естественным интеллектом. В человеко-машинных системах предполагается следующее разделение функций человека и машины: машина хранит и перерабатывает большие массивы информации, осуществляет информационное обеспечение принятия решений человеком; человек принимает управленческие решения.

Чаще в человеко-машинных системах компьютеры выполняют рутинную, нетворческую, трудоемкую переработку информации, освобождая человеку время для творческой деятельности. Однако целью развития компьютерной (информационной) технологии управления является полная автоматизация деятельности, включающая частичное или полное освобождение человека от необходимости принятия решений. Это связано не только со стремлением разгрузить человека, но и с тем, что развитие техники и технологий привело к ситуациям, когда человек в силу присущих ему физиологических и психических ограничений просто не успевает принимать решения в реальном масштабе времени протекания процесса, что грозит катастрофическими последствиями. Примеры - необходимость включения аварийной защиты ядерного ректора, реакция на события, проистекающие при запусках космических аппаратов и т.д.

Система, заменяющая человека, должна будет обладать интеллектом, в какой-то мере подобным человеческому - искусственным интеллектом. Исследовательское направление в области систем искусственного интеллекта также относится к кибернетике, однако вследствие его важности для перспектив всей информатики в целом мы рассмотрим его в отдельном параграфе.

ФУНКЦИИ ВВОДA-ВЫВОДА

Средства ввода-вывода не являются составной частью языка Си. Имеется ряд библиотечных функций Си. обеспечивающих стандартною систему ввода-вывода для программ на Си. Макроопределения, описания переменных и определения этих функций содержатся в файле стандартных заголовков stdio h Поэтому, как указывалось выше, каждая пользовательская программа должна содержать в начале ссылку

#include <stdio.h>.

В примерах программ мы неоднократно использовали форматные функции ввода (scanf()) и вывода (printf()). Набор стандартных функций ввода и вывода значительно шире и включает большое число функций для работы с данными различного типа, различными устройствами, буферизованного и небуферизованного, форматного и бесформатного ввода и вывода.

Система ввода-вывода Си обеспечивает некоторый уровень абстракции между программистом и используемым устройством. Эта абстракция называется потоком, а фактическое устройство ввода-вывода называется файлом. Буферизованная файловая система преобразует каждое физическое устройство в логическое устройство, называемое потоком. Существуют потоки двух типов: текстовые и двоичные.

Текстовый поток - это последовательность символов, которая организуется в строки, завершающиеся символами новой строки. Обработка текстового потока предполагает преобразование данных из текстового (внешнего) представления в машинное (внутреннее) или наоборот. При обработке двоичного потока последовательность его байтов взаимно однозначно соответствует байтам во внешнем устройстве.

В языке программирования Си файл - это логическое понятие, которое система может относить к чему угодно (от дисковых файлов до терминалов). Поток связывается с конкретным файлом выполнением операции «открыть» Как только файл открывается, можно обмениваться информацией между ним и программой. Закрытие выводимого потока заставляет ЭВМ записывать содержимое этого потока на внешнее устройство Этот процесс обычно называется промыванием потока. В начале выполнения программы ЭВМ открывает три предопределенных текстовых потока stdin, stdout и stderr, связанных со стандартными устройствами ввода-вывода (консоль - клавиатура и дисплей).
Допускается переадресация ввода-вывода к другим устройствам.

Простейшими функциями консольного ввода-вывод являются функция getche(), которая читает символ с клавиатуры, и функция putchar(), которая печатает символ на экране. Функция getche() ждет, пока не будет нажата клавиша, а затем возвращает ее значение, автоматически выдавая на экран «эхо» нажимаемой клавиши. Функция putchar() записывает ее символьный аргумент на экран в текущую позицию курсора.

Ниже приводится пример простой программы, которая принимает один символ с клавиатуры и выводит его на экран.

Программа 106

#include<stdio.h>

main()

(

char ch;

ch = getchar() ;

putchar(ch);

)

Есть две важные версии функции getche(). Первая – getchar() - буферирует ввод до тех пор, пока не введен возврат каретки. Второй версией является функция getch(), которая работает точно так же, как getchar(), за исключением того, что getch() не возвращает на экран эхо введенного символа.

Функции gets() и puts() позволяют читать и писать цепочки символов (строки) с консоли. Функция gets() читает цепочку символов, которая вводится с клавиатуры (ввод оканчивается возвратом каретки), помещает ее с адреса, который указывает ее аргумент - указатель символа. Функция puts() выводит на экран ее аргумент - цепочку символов, а затем символ новой строки. Например, нижеследующая программа читает цепочку в массив str и тут же печатает ее.

Программа 107

main ()

(

char str[80] ;

gets (str) ;

puts(str) ;

)

Функция puts() занимает меньше памяти и работает быстрее, чем printf() при выводе символьных цепочек, поэтому программисты часто используют функцию puts() в тех случаях, когда важно иметь высоко минимизированный код.

Таблица 3.4

Некоторые функции буферизованной сисгемы ввода-вывода

Имя	Функция
fopen() fclose() putc() getc() fseek() fprintf() fscanfl() feof() ferror() rewind() remove()	Открывает поток Закрывает поток Выводит символ в поток Вводит символ из потока Ищет указанный байт в потоке Форматный вывод в поток Форматный ввод из потока Возвращает истину, если достигается метка EOF (конец файла) Возвращает истину, если встретилась ошибка Устанавливает начальную позицию файла Стирает файл

<


Для работы с файлами в Си используются функции буферизованной системы ввода-вывода, табл. 3.4. Обращение к ним использует указатель файла, который определяет различные характеристики файла, включая его имя, статус и текущую позицию; используется связанным с этим файлом потоком для привязки каждой функции буферированного ввода-вывода к месту, над которым она выполняет свои операции. Указатель файла является переменной типа FILE, которая определяется в файле заголовков stdio.h.

Функция fopen() вызывается так:

fореn(<имя_файла>, <режим>);

Имя файла должно быть цепочкой символов, которая составляет правильное имя файла для операционной системы и может включать спецификацию пути. Режим задает желаемый статус открытия, табл.3.5.

Таблица 3.5

Значения режимов в Турбо-Си

Режим	Смысл
"r" "w" "а" "r+" "w+" ''а+"	Открыть файл для чтения Создать файл для записи Добавлять в файл Открыть файл для чтения/записи Создать файл для чтения/записи Открыть или создать файл для чтения/записи

Например, для того чтобы открыть файл с именем test для записи, можно написать

fp = fopen("test", "w");

где fp -переменная типа FILE*. Переменная fp является указателем файла.

Следующий оператор обнаруживает любую ошибку при открытии файла, такую, как, например, попытку открыть защищенный от записи диск или заполненный диск, прежде чем состоится попытка записи на него:

if((fp = fopen("tesf, "w"))==NULL)

{

рuts("Нельзя открыть файл!\n");

exit(l);

}

NULL - это макро, которое определяется в файле заголовка stdio.h.

Функция putc() в виде

рuts(<символ>, fp);

используется для записи символа в поток, который предварительно открыт для записи с помощью функции fopen(); fp - возвращаемый функцией fopen() указатель файла.

Функция getc() в виде

getc(fp)

используется для чтения символов, которые она возвращает из потока, открытого в режиме чтения функцией fopen().


fp является указателем файла типа FILE, который возвращается функцией fopen(). В тех случаях, когда достигается конец файла, функция getc() возвращает маркер его конца EOF. Например, для чтения текстового файла до маркера конца файла можно использовать следующие операторы:

ch = setc(fp);

while(ch!=EOF)

{

ch = getc(fp);

}

Функция feof() использует аргумент указателя-файла и возвращает 1, если достигнут конец файла, или 0, если не достигнут. Например, приведенная ниже программа читает двоичный файл до тех пор, пока ЭВМ не встречает маркер конца файла:

while(!feof(fp)) ch = getc(fp);

Функцию fdose() используют для закрытия потока, который был открыт с помощью функции foреn(). Все потоки необходимо закрыть перед завершением программы. Аргументом функции является указатель файла, который закрывается.

Функции foреn(), getc(), putc() и fdose() составляют минимальный набор функций ввода-вывода. Простым примером использования функций putc(), foреn() и fdose() является программа, которая приведена ниже. Эта программа просто читает символы с клавиатуры и записывает иx в дисковый файл до тех пор, пока не введен знак $. Имя выходного файла задается из командной строки. Например, если вы назовете программу ktod («клавиша - на диск»), то набор на клавиатуре ktod test будет позволять вам вводить строки текста в файл с именем test.

Программа 108

#include

.h"

main(argc,argv)                      /*ktod

- клавиша на диск */

int argc;

char *argv[];

(

FILE *fp;

char ch;

if(argc!=2)

{

printf("Bы забыли ввести имя файла\n);

exit(l);

)

if((fp=fopen(argv[l], "w"))== NULL)

(

printf("He может открыть файл\n);

exit(l);

}

do

(

ch = getchar();

putc(ch, fp);

)

while (ch!='s');

fclose (fp) ;

}

Еще одним примером является программа dtos, которая будет читать любой ASCII файл и выводить его содержимое на экран.

Программа 109

#include "studio.h"

main (argc, argv)         /*dtos-wicK на экран*/



int argc;

char *argv[] ;

(

FILE *fp;

char ch;

if(argc!=2) {

printf("Вы забыли ввести имя файла\n"};

exit(l);

}

if((fp=fopen(argv[l], "r"))==NOLL)(

printfC'He может открыть файл\n"};

exit(l);

}

ch=getc(fp);          /* читать один символ */

while(ch!=EOF)

{

putchar(ch);     /* печать на экран */

ch=getc(fp);

}

fclose(fp) ;

}

Под управлением буферизованной системы ввода- вывода можно выполнять операции чтения и записи с произвольным доступом с помощью функции fseek(), которая устанавливает файловую позицию.

Например, для чтения 234-го байта в файле с именем test можно использовать следующую функцию:

funcl()

{

FILE *fp;

if((fp=fopen("test" ,"r"))==NULL)

{

printf("He могу открыть фаил\n");

exit(l);

}

fseek(fp,234L,0);

return getc(fp); /*читать один символ в 234-й позиции*/

}

В дополнение к рассмотренным до сих пор основным функциям ввода-вывода буферизованная система ввода-вывода включает функции fprintf() и fscanf(). Эти функции ведут себя точно так же, как функции printf() и scanf(), за исключением того, что они работают с дисковыми файлами. Обращения к функциям fprintf() и fscanf() имеют следующий вид:

fprintf(1р,<формат>,<список аргументов>);

fscanf(1р,<формат>,<список аргументов>);

где fp является файловым указателем, который возвращается вызовом функции fopen().

ГЕОИНФОРМАЦИОННЫЕ СИСТЕМЫ

Когда о человеке говорят «он прочно стоит на земле», то имеют в виду не только прямой смысл этих слов, но и нечто основательное в характере, положении, профессиональной квалификации. В информации, окружающей нас, тоже удивительно много «стоит на земле», хотя мы не всегда об этом задумываемся. Огромное количество практически необходимых знаний просто «подвисают», не будучи привязанными к тому участку земли, информацию о котором они несут. Те информационные системы, которые хранят эти знания, позволяют их актуализировать, сопоставлять, использовать для решения прикладных задач, называются географическими информационными системами, короче-геоинформационными системами (ГИС).

Как и многие виды информационных систем, ГИС уходят корнями в 60-е годы нашего века. Однако, их истинный расцвет состоялся лишь тогда, когда появились адекватные технические средства - огромные по емкости и скорости доступа носители информации и высококачественные графические визуальные устройства отображения информации - ведь в ГИС почти все разыгрывается на фоне географической карты. В нашей стране ГИС еще только «становятся на ноги»; специалисты предрекают им большое будущее.

Приведем пример возможной ГИС. Муниципальная ГИС большого города (прообразы таковых имеются и в России) обслуживает всех тех, для кого информация привязана к месту ее нахождения в городе: городские власти, архитектурное управление, транспортников, предприятия по обслуживанию городских коммунальных сетей, энергетиков, связистов, работников торговли (магазинов, торговых баз), милицию, медицинские службы (особенно скорой помощи), налоговые службы, строительные организации, санитарно-эпидемиологические службы, органы социальной защиты и т.д. - всех трудно перечислить, ибо современный город является сложным социальным, экономическим и техническим образованием, и количество служб и учреждений, поддерживающих его жизнедеятельность, велико. Почти всегда нужная им информация привязана к карге города - как проехать скорой помощи, где произошел выброс вредных веществ и куда они распространяются, где перекрыгь трубопровод при аварии, в каком состоянии транспортные магистрали и как проехать, если некоторые из них временно перекрыты, и прочее, и прочее.
Потенциальный клиент такой ГИС - как любая городская служба, так и рядовые граждане, которые используют ее как информационно-справочную систему.

Для развертывания такой ГИС необходимо решить рад сложных и дорогостоящих организационных задач, в том числе

• создания и ведения регулярно обновляемой цифровой ^компьютерной) топографической основы;

• организации согласованного обновления пространственной информации, собираемой различными ведомствами;

• создания общегородских классификаторов основных структурных единиц города (улиц, микрорайонов и т.д.);

• создания единого координационного центра для ведения муниципальной ГИС.

По-видимому, муниципальный уровень является самым низким, на котором возможно создание многоцелевой ГИС того типа, который описан выше. На уровне региона или государства в целом информация столь велика по объему и столь тематически многообразна, что целесообразно создание тематических ГИС. Одной из важнейших задач, для решения которых такие региональные и общегосударственные ГИС должны быть вскоре разработаны, является создание государственного земельного кадастра, производимое на основе постановления правительства по федеральной целевой программе, принятой в августе 1996 г. Слово «кадастр» означает реестр, содержащий сведения об объекте. Цель разработки земельного кадастра - способствовать проведению единой политики в области земельных отношений, обеспечению интересов государства и населения страны, создание цивилизованного рынка земли, защиты прав ее владельцев, арендаторов и т.д. Информация эта колоссальна по объему и требует постоянной актуализации, фиксирующей все изменения в сфере землепользования.

Создание ГИС может быть и объектом международного сотрудничества. Так, в период 1993 - 96 гг. усилиями шести стран создана ГИС «Черное море». Будучи жизненно важным для нескольких стран, море претерпевает катастрофические изменения, приводящие к сокращению и гибели целых экосистем. ГИС «Черное море» включает огромный объем картографической информации (более 2000 карт), базы данных по геологии, метеорологии, физической океанографии, загрязнениям, биоресурсам, рыбным ресурсам.


Таким образом, государственные органы прибрежных стран, научные работники, да и просто все заинтересованные в судьбе моря получили возможность доступа к комплексу информации о нем.

Не следует думать, что каждая ГИС является столь огромной. Достаточно широкое распространение получили, так называемые, настольные ГИС. Они также хранят картографическую информацию и базы данных, привязанные к ней, но в гораздо более локальных вариантах. Скажем, для автовладельца большой интерес может представить ГИС, содержащая сведения о дорогах в районе, их покрытиях (асфальтовые, грунтовые и т.д.).

Рис. 6.11. Типовая структура ГИС

Для создания ГИС используют специализированные инструментальные программные средства, различные для разных классов ГИС. «Тяжелые» профессиональные системы типа Intergraph не предназначены для персональных компьютеров (хотя и существуют их усеченные версии). Для создания локальных ГИС на ПК существуют специальные программные средства, работающие в среде MS Windows. Так, отечественные программы GeoDraw и GeoGraph 1.5 позволяют создать ГИС на основе многослойной топологической модели географических данных. Такая модель позволяет описать не только координаты объектов, но и их качественные характеристики (например, взаимное расположение), что важно при преобразованиях изображений. К каждому слою изображения может быть подключено несколько таблиц баз данных; наоборот, каждая таблица может быть подключена к нескольким слоям. Пользователь этой инструментальной системы может наполнить ее конкретным содержанием, рис. 6,11.

Особой проблемой в ГИС является ввод графической (особенно картографической) информации и выбор ее форматов. Если ввод карты может быть осуществлен сканированием, то, в отличие от многих других задач хранения, обработки и вывода изображений, растровый формат изображения, создаваемый при сканировании, в ГИС менее удобен, чем векторный. Дело в том, что графическая информация в ГИС часто подвергается манипуляциям типа «растянуть», «сжать» и более сложным геометрическим преобразованиям.Поэтому первоначальное растровое изображение в ГИС-системах обычно подвергается векторизации, т.е. установлению геометрических и формульных соотношений между линиями и точками, образующими изображение.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНФОРМАТИКИ

Нет столь великой вещи, которую не превзошла бы еще большая.

Козьма Прутков

ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ЭВМ

Многие вещи нам непонятны не потому, что наши понятия слабы, но потому, что сии вещи не входят в круг наших понятий

Козьма Прутков

ЯЗЫКИ И МЕТОДЫ ПРОГРАММИРОВАНИЯ

Прохожий спросил у фермера, сооружающего небольшую деревянную постройку, что тот строит. - Пока не знаю, -ответил фермер. Если мне удастся сдать это сооружение, тогда оно - очаровательный сельский домик, а если не удастся, то это будет курятник.

Из журнала Reader's Digest

ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА

«... Ибо это недостойно совершенства Человеческого - подобно рабам тратить часы на вычисления».

Готфрид Вильгельм Лейбниц

§ ГЛОБАЛЬНЫЕ МОДЕЛИ РАЗВИТИЯ ЧЕЛОВЕЧЕСТВА

«Для человеческого ума недоступна совокупность причин явлений. Но потребность отыскивать причины вложена в душу человека. И человеческий ум, не вникнувши в бесчисленность и сложность условий явлений, из которых каждое отдельно может представляться причиною, хватается за первое, самое понятное сближение и говорит: вот причина».

Л. Н. Толстой. Война и мир, т.4, ч,2.

Рассмотренные выше модели представляли собой математические образы отдельных процессов и явлений. Каждая из них интересна по-своему, важна для конкретной науки или вида деятельности. Но все это по своей общечеловеческой важности уступает самому значимому для нас всех вопросу: каково ближайшее будущее человечества как вида в целом? Как будет развиваться мир в обозримом будущем?

Подчеркнем, что речь идет не о политических или экономических прогнозах для какой-то конкретной страны или общества - такие прогнозы, во-первых, в стабильных ситуациях тривиальны, а в нестабильных - мало что значат, а во-вторых, представляют собой интерес, в основном, для жителей этой страны или территории. Речь идет именно о человечестве в целом - какое у него (у нас всех, живущих на Земле) будущее?

Люди в текущей жизни имеют много конкретных проблем и мало склонны к таким общим размышлениям. Жизнь отдельного человека слишком коротка, и еще век-другой назад глобальные изменения в мире на протяжении жизни одного человека были не очень заметны - даже если он жил в достаточно бурную эпоху. Но в XX веке темпы событий ускорились так, как этого никогда не было в истории человечества, и мы стали все чаще слышать предсказания грядущих глобальных катастроф - гибель природы из-за промышленных загрязнений, невесть откуда взявшиеся «озоновые дыры» в защищающей нас от космических излучений стратосфере, истощение средств воспроизведения кислорода из-за массовой вырубки лесов и т.д. Хотя часть этих страхов нагнетается шарлатанами или заинтересованными в запугивании людей деятелями без каких-либо серьезных обоснований, это не означает отсутствия проблемы - наоборот, она более чем реальна.
Даже не столь катастрофические события - например, истощение природных ископаемых - может привести к совершенно радикальным переменам в образе жизни человечества, и при этом, в первую очередь, в странах, которые сегодня являются наиболее промышленно развитыми.

Будущее человечества определяется столь огромным количеством процессов, частично им контролируемых, частично нет, и эти процессы столь взаимосвязаны и имеют столь противоречивые последствия, что лишь математическое моделирование их во всей разумной совокупности, реализуемое на современных компьютерах, может дать качественно верный прогноз. При этом замечательно высказанная великим русским писателем мысль, вынесенная в эпиграф, никогда не должна забываться. Как бы велико ни было неизбежное огрубление реальности при таком моделировании, остаются столько обобщенных факторов «первого ранга», что проследить их неизбежную интерференцию не под силу даже самому могучему уму.

Такие модели, получившие название глобальных (всеохватывающих), начали возникать в 70-х годах нашего века. Наиболее известны модели МИР-1, МИР-2, МИР-3, сформулированные и изученные группой сотрудников Массачусетского технологического института (США) под руководством Д.Х.Медоуз и Д.Форрестера. Работы были начаты по поручению «Римского клуба» - международной неправительственной группы выдающихся государственных деятелей, ученых, бизнесменов. Результаты в свое время произвели в западном мире сенсацию, ибо большинство сценариев возможного развития событий вели к результатам, которые можно назвать концом света (разумеется, с точки зрения человечества). Вместе с тем авторы не раз подчеркивали, что речь идет не о заведомо предопределенном будущем, а о выборе путей развития человечества, среди которых есть и ведущие к стабильности.

Что является причиной возможной нестабильности? - Характерной чертой жизни человечества в эпоху после начала промышленной революции стал быстрый -часто экспоненциально быстрый - рост многих показателей. Период удвоения численности населения Земли составляет примерно 40 лет (наличие такого постоянного периода - характерная черта экспоненциального роста).


Биологи и экологи хорошо знают, что экспоненциальное наращивание численности популяции чаще всего кончается катастрофой - истощаются источники, поддерживающие ее существование. С точки зрения существования вида это не трагедия (кроме уникальных случаев, когда данный вид весь сводится к одной популяции). Однако, в наше время человечество израсходовало почти все ресурсы для экстенсивного роста и распространения «вширь». Объем промышленного производства в XX веке также растет практически экспоненциально с годовым темпом прироста в среднем 3,3%. Это приводит к истощению природных ресурсов - полезных ископаемых, чистой воды, чистого воздуха. Содержание в атмосфере одного из устойчивых соединений углерода (диоксида) в результате сжигания органического топлива и истощения лесов возросло с начала века на треть; потенциально это ведет к глобальному потеплению на Земле с самыми катастрофическими последствиями. Чем больше людей, тем больше необходимо продуктов питания, и мировой объем вносимых минеральных удобрений растет экспоненциально с периодом удвоения около 15 лет. Ясно и без всякого моделирования, что подобная жизнь с безудержным ростом всего и вся не может длиться долго — а ныне «долго» сопоставимо со сроком жизни двух-трех поколений.

В то же время для глобальных процессов характерно то, что каждый отдельно взятый процесс нельзя однозначно назвать «хорошим» или «плохим» с точки зрения влияния на судьбу человечества. Увеличение производства удобрений ведет к увеличению производства продуктов питания - «хорошо», но оно же ведет к уменьшению запасов чистой пресной воды, которую портят удобрения, попадающие через почву с дождями в реки и подземные источники, ведет к необходимости увеличения производства энергии для добычи удобрений и связанному с этим химическому и тепловому загрязнения почвы и атмосферы и т.д. - «плохо». Взвесить последствия всего этого на развитие человечества можно лишь при комплексном учете всех факторов разом.

В чем же заключаются возможности избежать катастрофических последствий для развития человечества? Были сформулированы следующие три правила, соблюдение которых необходимо для глобальной устойчивости (прийти к ней необходимо после прекращения нынешних процессов неконтролируемою роста).



1.Для возобновимых ресурсов (лес, вода, рыба и т.д.) темпы потребления не должны превышать темпов естественного восстановления.

2. Для невозобновимых ресурсов (уголь, нефть, руды и т.д.) темпы потребления не должны превышать темпов их замены на возобновимые (развитие солнечной и ветровой энергетики, посадка лесов и т.д.) и темпов развития новых технологий для обеспечения смены ресурсов для того, чтобы после исчезновения, к примеру, нефти был обеспечен приток энергии от нового ресурса.

3. Для загрязняющих веществ предельная интенсивность выбросов не должна превышать темпов, с которыми эти вещества перерабатываются или теряют вредные для окружающей среды свойства.

В настоящее время человечество отнюдь не руководствуется этими правилами (хотя и есть соответствующие попытки - например, соглашения о квотах на рыбную ловлю). Если в прошлые века это не представляло опасности для вида в целом, то в наши дни ситуация изменилась. Достаточно сказать, что если бы при сегодняшней численности населения Земли каждый человек потреблял бы столько энергии и других ресурсов, сколько их сегодня потребляет в среднем гражданин США (при существующих технологиях), это привело бы к немедленной вселенской катастрофе.

Модель WORLD-3 (МИР-3). Модель состоит из пяти секторов:

• стойкие загрязнения;

• невозобновимые ресурсы;

• население;

•сельское хозяйство (производство продуктов питания, плодородие земель, освоение земель);

• экономика (промышленное производство, производство услуг, рабочие места). Исходными являются первичные взаимосвязи, такие как

• численность населения и запасы промышленного капитала;

• численность населения и площадь возделываемых земель;

• площадь возделываемых земель и объем промышленного капитала;

• численность населения и капитал сектора услуг;

• капитал сектора услуг и промышленный капитал и т.д.

В каждом секторе прослеживаются все первичные взаимосвязи и выражаются математическими соотношениями. По мере необходимости учитываются процессы материального и информационного запаздывания, так как реакция, скажем, численности населения на улучшение питания является не мгновенной, а запаздывающей.


Это типично для большинства рассматриваемых процессов.

Модель WORLD-3 по приведенной в начале главы классификации носит черты дескриптивные и оптимизационные. Ее основное назначение - представить возможные пути достижения экономикой (в широком смысле термина) такой численности населения планеты, которая может поддерживаться окружающей средой неопределенно долгое время. Она не предсказывает нечто отдельное для России или Египта, не решает никаких локальных вопросов. Модель исходит из того, что на Земле существует глобальное сообщество.

Динамика численности населения - интегральная характеристика, которая вбирает в себя все факторы. Чисто умозрительно возможны два типа устойчивых динамик (непрерывный рост и «сигмоидное» приближение к равновесию) и три типа неустойчивых, связанных с выходом за пределы допустимого (колебания с последующим выходом на стационар, хаотические колебания и коллапс, т.е. исчезновение вида). Непрерывный рост представляется совершенно нереалистическим, последняя из неустойчивых динамик - трагедией для человечества, а за резкими колебаниями, как нетрудно догадаться, стоят войны, эпидемии, голод-то, что мы и без всяких моделей видим в реальности.

Типичные для модели WORLD взаимосвязи, находящие выражения математическими средствами (дифференциальными и «обычными» уравнениями) приведены на рис. 7.51. Он демонстрирует связи между численностью населения, промышленным капиталом, площадью возделываемых земель и загрязнением окружающей среды. Каждая стрелка на рисунке указывает наличие причинной связи, которая может быть непосредственной или запаздывающей, положительной или отрицательной.

Понятия положительной и отрицательной обратной связи взяты из теории автоматического регулирования (раздела кибернетики). Причинно-следственная связь между двумя элементами называется отрицательной, если изменение одного элемента передается второму, возвращается от него к первому и изменяет его в направлении, противоположном первоначальному (подавляет), и положительной, если это изменение, возвращаясь к первому, усиливает его.


Если элементов не два, а больше, то говорят о контуре обратной связи, через которую сигнал проходит по кругу, возвращаясь к источнику и влияя на него.

Некоторый набор таких рисунков графически исчерпывает модель WORLD. Однако, за каждой стрелкой - первичные взаимосвязи, за каждой из них - уравнения, в которые входит ряд параметров. Фактически именно значения этих параметров и определяют результаты решения, поэтому к их анализу привлекаются как многочисленные узкие специалисты, так и многие эмпирические (статистические) данные, собранные в десятках справочников, отчетов ООН и отдельных государств. Количество взаимосвязанных переменных в модели WORLD-3 равно 225, параметров - еще больше.

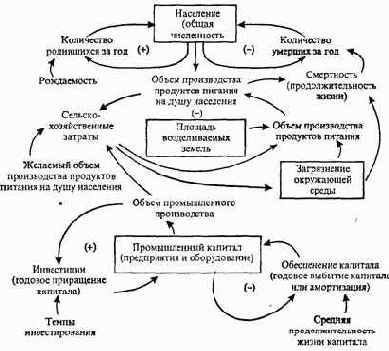
Рис. 7.51. Контуры обратных связей численности населения, капитала, сельскохозяйственного производства и загрязнения окружающей среды

Результаты глобального моделирования.

Опубликованные «сценарии» развития человечества, следующие из моделей WORLD, охватывают промежуток времени от 1900 до 2100 гг. Первые 90 лет, уже прошедшие, позволяют «настраивать» модель, понять степень ее достоверности.

Первый из сценариев основан на гипотезе, что все будет развиваться без серьезных изменений, глобальных политических катаклизмов, без особых усилий по сохранению ресурсов и уменьшению загрязнения окружающей среды. Весьма печальные результаты такого развития иллюстрирует рис. 7.52 (заимствовано из того же источника).

Разумеется, временные шкалы здесь весьма расплывчаты. Что будет, если на Земле обнаружатся и окажутся доступными (например, в океанах) дополнительные залежи нефти и газа, других ресурсов? Моделирование безжалостно утверждает, что это не изменит качественно характер эволюции, а лишь сдвинет вправо точки экстремумов кривых.

Вместе с тем модель WORLD позволяет нащупать пути регулируемого развития, которое ведет к плавному («сигмоидному») поведению основных переменных. Этот путь связан с самоограничениями и переходом на усовершенствованные промышленные и сельскохозяйственные технологии.Иллюстрацией тому является рис. 7.53.

Итак, математическое компьютерное моделирование вторгается даже в такую сверхзадачу, как самосохранение человека как вида.



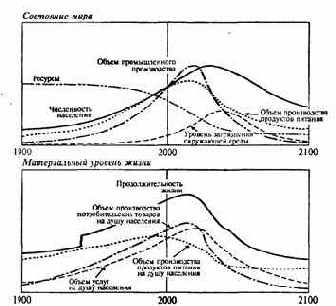
Рис. 7.52. Возможный вариант развития человечества на период 1900-2100 гг.



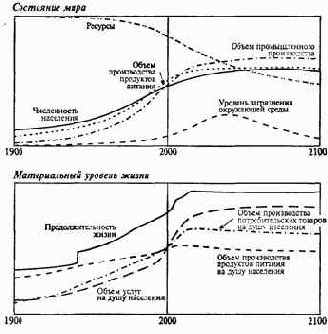
Рис. 7.53. Более оптимистичный вариант развития человечества на тот же период времени

ГРАФИЧЕСКИЕ РЕДАКТОРЫ

Создать объекты иллюстративной графики, включая динамические ролики, можно средствами программирования, а также графическими редакторами и системами. Рассмотрим два из них.

Редактор Paint

 

Графический редактор Paint, входящий в комплект стандартных программ MS Windows 95, позволяет, используя манипулятор «мышь», выполнять черно-белые и цветные рисунки, обрамлять их текстом, выводить на печать. В Paint можно рабо­тать с фрагментами графических изображений: копировать, перемещать, поворачи­вать, изменять размеры, записывать на диск и считывать с диска. С помощью Paint можно обрабатывать графические изображения, а также считывать и записывать в файл полностью или частично изображение с дисплея, если монитор работает в графическом режиме.

Рис. 2.18. Рабочее окно программы Paint

После загрузки пакета появляется рабочий экран редактора (рис. 2.18). Большую часть экрана занимает рабочее поле, окрашенное в фоновый цвет. Над рабочим полем - меню, позволяющее выполнять команды редактирования. Слева от рабоче­го поля расположена панель инструментов, на которой высвечен инструмент, в данный момент являющийся рабочим. Под рабочим полем находится палитра. С левого края палитры показаны два вложенных квадрата, внутренний из которых окрашен в рабочий цвет, а внешний - в фоновый. В левом нижнем углу экрана выводится калибровочная шкала, которая позволяет устанавливать ширину рабочего инструмента (кисти, резинки и т.д.). Установленная в данный момент ширина инструмента отмечена стрелкой. Вдоль нижнего правого и правого края рабочего поля находятся линейки прокрутки для перемещения рабочего поля по картинке, если размеры картинки больше размеров рабочего поля.

Общие правила работы с редактором таковы. Для выбора (установки) параметров работы и выполнения команд в Paintbrush необходимо поместить указатель мыши на пункт меню и щелкнуть левой кнопкой. Выход из программы: File/Quit.

Программа Freeze предназначена для сохранения выводимого на экран изображения в графическом PCX-файле с одновременным сохранением оформления экрана, возможностью последующего редактирования данного изображения и вставки его в качестве иллюстрации в текстовые редакторы и настольные издательские системы.
Установка программы происходит автоматически при запуске Paintbrush.

Редактор CorelDraw

Начиная работать с графическим редактором CorelDraw, мы прежде всего видим его рабочее окно, рис. 2.19.

Рис. 2.19. Рабочее окно программы CorelDraw

Чтобы активизировать меню выбора (установки) параметров

работы или выполнения команд, установите указатель мыши на пункт меню и щелкните левой кнопкой или нажмите клавишу Alt и клавишу, соответствующую выделенной букве. В некоторых случаях для облегчения выполнения наиболее часто употребляемых команд ввод их с клавиатуры осуществляется нажатием комбинации клавиш или определенной клавиши. Выполнение команд происходит после подтверждения правильности установки всех параметров или выбора значений активизацией экранной кнопки ОК в диалоговой панели или нажатием клавиши Enter.

Выход из меню - переместить указатель мыши за пределы меню и щелкнуть кнопкой или нажать клавишу Esc.

Выход из программы: File/Quit или Alt + F4.

Для вызова диалоговой панели выбора (установки) параметров работы или выполнения команд необходимо установить указатель мыши на пункт меню или команду и щелкнуть кнопкой или нажать клавишу Alt и клавишу, соответствующую выделенной букве. Выполнение команд происходит после подтверждения правильности установки всех параметров (выбора значений) активизацией экранной кнопки ОК или нажатием клавиши Enter.

Для редактирования рисунка следует активизировать пиктограмму с помощью мыши или нажатием клавиши Пробел, переместить указатель на любую точку контура рисунка и щелкнуть кнопкой. Выбранный рисунок будет окружен восемью квадратами черного цвета. Можно выделить одновременно несколько объектов, последовательно выбирая их с помощью мыши при нажатой клавише Shift или отмечая на экране прямоугольную область, в которой они расположены. Для одновременного выбора всех рисунков на экране необходимо активизировать пиктограмму, переместить указатель мыши в один из углов выбираемого прямоугольного контура, нажать кнопку и, не отпуская ее, переместить указатель в противоположный угол и отпустить кнопку.


Контур будет изображен штриховой линией. Для отмены выбора - переместить указатель мыши за контур и щелкнуть кнопкой.

Для изменения масштаба выводимого на экран рисунка необходимо активизировать соответствующую пиктограмму.

Работа с текстом

начинается с активизации пиктограммы текста. Для перемещения по тексту в диалоговой панели Техt необходимо переместить указатель мыши и щелкнуть левой кнопкой. Однако в программе для перемещения предусмотрены также специальные клавиши.

Для выделения фрагмента текста необходимо активизировать пиктограмму с помощью мыши или клавиши Пробел. Переместите указатель мыши в один из углов выбираемого прямоугольного контура, нажмите кнопку К, не отпуская ее, переместите указатель в противоположный угол, отпустите кнопку. Весь контур будет окружен штриховой линией. Для выделения отдельного символа 'необходимо активизировать пиктограмму, переместить указатель мыши в один из углов выбираемого прямоугольного контура, нажать кнопку и, не отпуская ее, переместить указатель в противоположный угол. Выбранный объект не будет окружен рамкой из квадратов, однако на нем будут выделены все узловые точки. Выбор нескольких символов осуществляется аналогично при нажатой клавише Shift.

Прежде чем начать оформление ранее введенного текста, его необходимо выделить одним из выше описанных способов.

ГРАФИЧЕСКИЕ ВОЗМОЖНОСТИ

Для получения графических образов необходимо задать графический экран (например, SCREEN 9) и масштаб или окно экрана WINDOW (х1,у1) - (х2,у2). Здесь (х1,у1), (х2,у2) - координаты угловых точек экрана, расположенных на диагонали. Если ограничиться этим, то цвет фона будет черным. Для задания фона другого цвета используется оператор COLOR zl, z2, где zl- цвет текста, z2- цвет фона. Например, зададим графический экран, с размерами по горизонтали и по вертикали, соответственно 32 и 24 единицы, с началом координат в центре экрана. Цвет фона- синий (z2=l), а цвет надписей -желтый (zl=14).

10 *********** иыгтый лист *********************

20 SCREEN 9

30 WINDOW (-16,-12)-(16, 12)

40 COLOR 14,1

Изображение точки с координатами (х,у) и заданным цветом осуществляется командой PSET(x,y),z. Здесь z - номер цвета. Точку на бумаге можно изобразить маленьким кружком. Иногда, когда требуется изображение точки покрупнее, буквально рисуют кружок и закрашивают его В этой связи, изображение точки на экране дисплея можно создавать, выводя образ окружности и закрашивая ее в тот или иной цвет. Для создания окружности используется оператор CIRCLE (\,y),r,z, где х,у - координаты центра окружности, г - радикс окружности, z - номер цвета окружности. Закрашивают окружность оператором PAINT (x,y),zl,z , где zl - номер цвета которым закрашивают, z - номер цвета окружности.

Пример. При запуске программы на экране появятся 4 «точки» в )гла\ квадрата 10*10, окрашенные в зеленый цвет (10), и пятая «точка» красного цвета (12) вдвое большего размера в центре экрана Их границы окрашены в белый цвет (15).

Программа 61

10 '**************** Точки *********************

20 SCREEN 9

30 WINDOW (-16,-12) - (16,12)

40 COLOR 14, 1

50 '********** изображение точек *********************

60 CIRCLE (-5, -5). .25, 15 : PAINT (-5, -5), 10, 15

70 CIRCLE (-5, 5), .25, 15 : PAINT (-5, 5), 10, 15

80 CIRCLE (5, 5), .25, 15 : PAINT (5, 5), 10, 15

90 CIRCLE (5, -5), .25, 15 : PAINT (5, -5), 10, 15

100 CIRCLE (0, 0), .5, 15 : PAINT (0, 0), 12, 15

Допустим, что в компьютерной демонстрации надо обратить внимание на какую-либо точку графического образа. В этом сл>чае точку делают мигающей. Для этого меняют с определенной частотой ее цвет.

Программа 62

10 '*************** чистый лист **********************

20 SCREEN 9

30 WINDOW (-16, -12) - (16, 12)

40 COLOR 14, 1

50 '*************** мигающая точка *******************

60 FOR 1=1 TO 5

70 CIRCLE (0. 0), .5, 15 : PAINT (0, 0), 14, 15 : DELAY .2

80 'FOR k=l TO 200 : NEXT k

90 CIRCLE (0, 0),.5, 15 : PAINT (0, 0), 12, 15 : DELAY .5

100 'FOR k=l TO 500 : NEXT k

110 NEXT I

Обратим внимание на то, что в этой программе время выдержки красного цвета (12) полсекунды (DELAY .5, либо пустой цикл), а желтого цвета (14) - две десятых секунды. В результате получается красная мигающая точка.

Для акцентирования внимания мигание точки можно сопроводить звуковыми сигналами. Для этого используют оператор ВЕЕР стандартной частоты и длительности. Для издания звукового сигнала заданной частоты и длительности применяют оператор SOUND cl,t, где cl - частота сигнала, t -длительность.

Программа 63

10   ************** Клаксон **************************

20 SCREEN 9

30 WINDOW (-16, -12) - (16,12)

40 COLOR 14, 1

110 '***** мигающие точки со звуковым сигналом ВЕЕР *******

120 FOR i=l TO 5

130 CIRCLE (-5, -5), .25, 15 : PAINT (-5, -5), 6, 15

140 CIRCLE (-5, 5), .25. 15 : PAINT (-5, 5), 6, 15

150 CIRCLE (5, 5), .25, 15 : PAINT (5, 5). 6, 15

160 CIRCLE (5, -5), .25, 15 : PAINT (5, -5), 6, 15

170 DELAY .2 : BEEP

180 CIRCLE (-5, -5), .25, 15 : PAINT (-5, -5), 10, 15

190 CIRCLE (-5, 5), .25, 15 : PAINT (-5, 5), 10, 15

200 CIRCLE (5. 5), .25, 15 : PAINT (5, 5), 10, 15

210 CIRCLE (5, -5), .25, 15 : PAINT (5, -5). 10, 15

220 DELAY .5

230 NEXT i

240 '***** Мигающая точка со звуковым сигналом SOUND ******

250 FOR i=l TO 5

260 CIRCLE (0, 0), .5, 15 : PAINT (0, 0), 14, 15

270 SOUND 600, .2 : DELAY .2



280 CIRCLE (0,0), .5, 15 : PAINT (0, 0), 12, 15

290 SOUND 300, .5 : DELAY .5

300 NEXT i

В следующем примере демонстрируется работа с окружностями и эллипсами, которые достаточно часто встречаются в графических образах различных объектов. Изображение окружности или дуги окружности выводится тонкими линиями с помощью оператора CIRCLE.

Программа 64

 '************0кружности и дуги **********************

20 SCREEN 9

30 WINDOW (-16,-12) - (16,12)

40 COLOR 14,1

50 г*************** задание числа PI ****************

60 pi=4*atn(l)

iq >********** изображение окружности и дуг **********

80 CIRCLE

(0, 0), 4, 15

90 CIRCLE (5. 5), 4, 14, 0, pi/2 'дуга в первой четверти

100 CIRCLE

(-5, 5). 4, 14. pi/2, pi

'во второй

110 CIRCLE

(-5,-5) ,4, 14, 0, pi, 3*pi/2 'в третьей

120 CIRCLE

(5,-5), 4, 14, 3*pi/2,2*pi 'в четвертой

Для изображения линий используется оператор LINE, который строит линии одной и той же толщины. Однако, при создании графических образов в компьютерных Демонстрациях требуются линии различной толщины. Например, выделяются оси координат на фоне координатной сетки или рисуется график линейной зависимости и т.д. Существует очень быстрый способ получения изображений вертикальных и горизонтальных линий различной толщины. Это достигается выводом на экран узких прямоугольников. Этот прием иллюстрируется на примере построения осей координат:

LINE(-16.-.l)-(16,.l),15,bf LINE(-.l,-12)-(.l,12),15,bf

Линии произвольной формы и толщины, в том числе и прямые, выводятся на экран дисплея при помощи оператора CIRCLE. Заключенный в цикл с достаточно малым шагом, оператор CIRCLE действует аналогично плакатному перу с шириной линии, равной диаметру окружности:

FOR х =-4 ТО 4 STEP .01

у = 0.5*\''2

CIRCLE (x,y),.1,15 NEXTx

Если требуется провести очень тонкую линию, то вместо CIRCLE используется оператор PSET (\,y). z, где z - номер цвета, а (х,у) - координаты точки (PSET -точка). Иногда изображения соседних точек соединяют отрезками прямых линий. График функции в этом случае будет представляться ломаной линией.



Программа 65

I ********* тонкие линии и ломаные кривые ************

10 SCREEN 9

20 WINDOW (-16,-12) - (16,12)

30 COLOR 14,1

4о у**************** тонкая линия ********************

50 FOR х = -15 TO 15 STEP .01

60 у = 3*sin(x/3)

70 PSET (х, у+7), 14

80 NEXT х

90 г**************** ломаная линия - 1 ***************

100 FOR х = -15 TO 15 STEP .1

110 у = 3*sin(x/3)

120 PSET (x,y), 11

130 IF x>-15 THEN LINE (x,y) - (xl.yl), 11

140 у1=-У : xl=x

150 NEXT

х

160 ***************** ломаная линия - 2 ***************

170 FOR х = -15 TO 15.STEP .1

180 у = 3*sin(x/3)

190 CIRCLE

(х, у-7), .1, 15

200 IF x>-15 THEN LINE (х, у-7) - (xl, yl- 7), 10

210 CIRCLE (xl, yl- 7), .1, 15 : PAINT (xl.yl - 7), 14, 15

220 у1=У : х1=х

230 NEXT х

340 '********************** Оси ***********************

250 LINE (-16, 7) - (16, 7), 15

260 LINE (-16, 0) - (16, 0), 15

270 LINE (-16, -7) - (16, -7), 15

Выше упоминалось о способе закрашивания областей, ограниченных линией одного цвета, с помощью оператора PAINT. Оператор LINE (\l,yl)-(x2,y2),z,bf позволяет получать закрашенные прямоугольники. Существуют специальные приемы закрашивания. Они основаны на повторении оператора, закрашивающего элементарную площадку. Причем, это может производиться либо по определенному закону, либо случайным образом. Ниже приведена программа, иллюстрирующая два способа закрашивания (хотя можно придумать и другие).

Программа 66

10 **************** закрашивание **********************

20 SCREEN 9

30 WINDOW

(-16, -12) -(16, 12)

40 COLOR

14, 1

50 '************ постепенное закрашивание ************

60 LINE (-10.1, -5.1) - (10.1, 5.1), 15, b

70 FOR x = -10 TO 10 STEP .01

80 LINE (x, -5) - (x, 5), 12

90 NEXT x

100 DELAY 2 : ' FOR k=l to 2000 : NEXT k

110 CLS

120 'а*************** гаситель экрана *****************

130 FOR i = 1 ТО 2000

140 x = .5*INT(RND*64) - 16

150 у = INT(RND*24) - 12

160 LINE

(x, у) - (Х+.5, у+1), 15, bf

170 NEXT i

Следующая программа аналогична программе 31 на Паскале и строит столбчатую диаграмму, наглядно отражающую числовую информацию о населении 6 крупных городов мира: Токио, Гамбурга, Москвы, Бангкока, Мехико и Парижа.



Программа 67 (см. программу 31)

Ю **************** столбчатая диаграмма ****************

20 SCREEN 9

30 COLOR 14, 1

40 DATA 11500, 2300, 9700, 5100, 12400, 8200

45 DATA "Токио", "Гамбург", "Москва", "Бангкок", "Мехико", "Париж"

50 LINE (40, 300) - (550, 300): LINE (40, 300) - (40, 20)

60 FOR k = 1 ТО б

70 READ m(k)

80 NEXT k

90 a = m(l)

100 FOR k = 2 TO 6

110 IF m(k) > a THEN a = m(k)

120 NEXT k

130 FOR k = 1 TO 6

140 READ name$(k)

150 NEXT k

160 FOR k = 1 TO 6

170 n =

10 * k + 3

180 LOCATE 23, n: PRINT name$(k)

190 m(k) = 300 - m(k) / a * 200

200 LINE (k * 80, 300) - (80 + k * 80, 300 - m(k)), k + 3, BF

210 NEXT k

220 c$ = HEX$(a)

230 LOCATE 3, 1: PRINT c$

240 c$ = HEX$(0)

250 LOCATE 22, 3: PRINT c$ 260 END

Дадим короткие пояснения к использованным в данной программе и не использовавшимся ранее средствам. В представленном примере использован не встречавшийся ранее оператор LOCATE X,Y, останавливающий курсор на позицию х,у координатной сетки дисплея. Сочетание команд LOCATE ... PRINT позволяет выводить на экран, находящийся в графическом режиме, тексты. Функция HEXS преобразует числа в соответствующие символы. Отсутствие команды WINDOW приводит к максимально возможному графическому окну.

ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ АЛГОРИТМОВ

Алгоритм, составленный для некоторого исполнителя, можно представить различными способами: с помощью графического или словесного описания, в виде таблицы, последовательностью формул, записанным на алгоритмическом языке (языке программирования). Остановимся на графическом описании алгоритма, называемом блок-схемой. Этот способ имеет ряд преимуществ благодаря наглядности, обеспечивающей, в частности, высокую «читаемость» алгоритма и явное отображение управления в нем.

Прежде всего определим понятие блок-схемы. Блок-схема - это ориентированный граф, указывающий порядок исполнения команд алгоритма; вершины такого графа могут быть одного из трех типов (рис. 1.12).

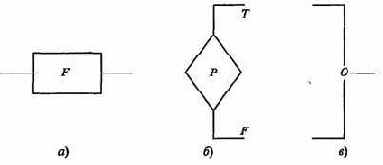
Рис. 1.12. Три типа вершин графа

На рис. 1.12 изображены «функциональная» (a) вершина (имеющая один вход и один выход); «предикатная» (б) вершина, имеющая один вход и два выхода (в этом случае функция Р передает управление по одной из ветвей в зависимости от значения Р (Т,

т.е. true, означает «истина», F, т.е. false - «ложь»); «объединяющая» (в) вершина (вершина «слияния»), обеспечивающая передачу управления от одного из двух входов к выходу. Иногда вместо Т пишут «да» (либо знак +), вместо F- «нет» (либо знак -).

Из данных элементарных блок-схем можно построить четыре блок-схемы (рис. 1.13), имеющих особое значение для практики алгоритмизации.

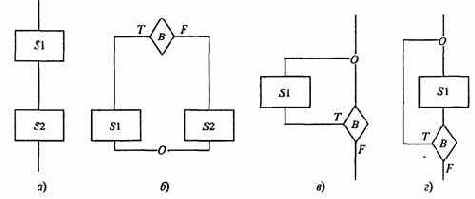
Рис. 1.13. Основные алгоритмические структуры

На рис. 1.13 изображены следующие блок-схемы: а -

композиция, или следование; б - альтернатива, или развилка, в

и г -

блок-схемы, каждую из которых называют

итерацией, или циклом

(с предусловием (в), с постусловием (г)). S1 и S2 представляют собой в общем случае некоторые серии команд для соответствующего исполнителя, В - это условие, в зависимости от истинности (Т) или ложности (F) которого управление передаётся по одной из двух ветвей. Можно доказать, что для составления любого алгоритма достаточно представленных выше четырех блок-схем, если пользоваться их последовательностями и/или суперпозициями.

Блок-схема «альтернатива» может иметь и сокращенную форму, в которой отсутствует ветвь S2 (рис. 1.14, а). Развитием блок-схемы типа альтернатива является блок-схема «выбор» (рис. 1.14, б).

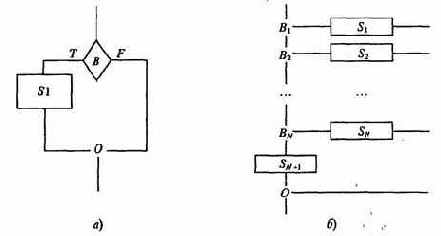
Рис. 1.14. Развитие структуры типа «альтернатива»;

о) - неполная развилка; б) -

структура «выбор»

На практике при составлении блок-схем оказывается удобным использовать и другие графические знаки (некоторые из них приведены на рис. 1.15).

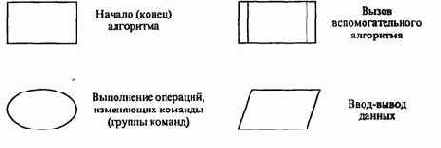
Рис. 1.15. Некоторые дополнительные конструкции для изображения блок-схем алгоритмов

ГРАММАТИКА ЯЗЫКОВ ПРОГРАММИРОВАНИЯ

Описанию грамматики языка предшествует описание его алфавита. Алфавит любого языка состоит из фиксированного набора символов, однозначно трактуемых. Алфавит языков программирования, как правило, связан с литерами клавиатуры печатной машинки. Клавиатуры персональных компьютеров близки к ним по наличию литер.

Алфавиты большинства языков программирования близки друг другу и основываются на буквах латинского алфавита, арабских цифрах и общепринятых спецсимволах, таких как знаки препинания, математических операций, сравнений и обозначений. Большинство популярных языков программирования в своем алфавите содержат следующие элементы:

<буква> : : = AaBbCcDdEeFf и т.д.

<цифра> ::=0123456789

<знак арифметической операции >::=*/+-

<разделитель> ::=.,;:()[]{}':=

<служебное слово> :: = begin end if then else for next и т.д.

<спецсимвол> :: = <знак арифметической операции> | <разделитель> |

<служебное слово>

<основной символ>::=<буква> | <цифра> | <спецсимвол>

<комментарий>::=<любая последовательность символов>

Несмотря на значительные различия между языками программирования, ряд фундаментальных понятий в большинстве из них схожи. Приведем часть этих понятии.

Оператор - одно из ведущих понятий всех языков программирования (теоретически, за исключением чисто декларативных; но в действительности и они используют родственное понятие). Каждый оператор представляет собой законченную фразу языка и определяет однозначно трактуемый этап обработки данных В соответствии с теорией алгоритмов выделяют основные (базисные) операторы языка: присвоения, условный и безусловный переход, пустой оператор. К производным, не основным, относят составной оператор, оператор выбора, оператор цикла и оператор присоединения.

Все операторы языка в тексте программы отделяются друг от друга явными или неявными разделителями, например:

Sl;S2;...;Sn

Операторы выполняются в порядке их следования в тексте программы.
Лишь с помощью операторов перехода этот естественный порядок может быть нарушен.

Большая часть операторов ведет обработку величин. Величины могут быть постоянными и переменными. Значения постоянных величин не изменяются в ходе выполнения программы. Величина характеризуется типом, именем и значением. Наиболее распространенные типы величин - числовые (целые и вещественные), символьные, логические. Тип величины определяется ее значением.

Другая важная классификация величин - простые и структурированные. Простая величина в каждый момент может иметь не более одного значения. Ей соответствует одна ячейка памяти (поскольку термин «ячейка» несколько устарел, часто говорят «машинное слово») или ее эквивалент во внешней памяти компьютера. Структурированная величина, имея одно имя, может иметь разом несколько значений. Эти значения представляют собой элементы (компоненты) величины. Самый широкоизвестный пример - массив, у которого элементы различаются по индексам (номерам). Вопрос о структурировании величин - входных, выходных и промежуточных - для успеха решения прикладной задачи не менее важен, чем вопрос о правильном написании последовательности операторов.

Важнейшие характеристики структурированной величины таковы: упорядоченность (да или нет), однородность (да или нет), способ доступа к элементам, фиксированность числа элементов (да или нет). Так, массив является упорядоченной однородной структурой с прямым доступом к элементам и фиксированным их количеством.

Всем программным объектам в языках даются индивидуальные имена. Имя программного объекта называют идентификатором

(от слова «идентифицировать»). Чаще всего идентификатором является любая конечная последовательность букв к цифр, начинающаяся с буквы:

<идентификатор>::=<буква> | <идентификатор> | <буква>

 <идентификатор><цифра>

Как правило, в большинстве языков программирования в качестве идентификатора запрещается использовать служебные слова языка.

Многим слово «идентификатор» не нравится, и в настоящее время чаще употребляют слово «имя», поскольку



<имя>::=<идентификатор>.

Программисты выбирают имена по своему усмотрению. Принципы выбора и назначения имен программным объектам естественны. Следует избегать мало выразительных обозначений, не гоняться за краткими именами. Имена должны быть понятны, наглядны, отражать суть обозначаемого объекта. Например,

Summa, Time, i, j, integral, init и т. п.

Некоторым идентификаторам заранее предписан определенный смысл и их называют стантартными, например, Sin - это имя известной математической функции.

Описания или объявления программных объектов связаны с правилами обработки данных. Данные бывают разные и необходимо для каждого из них определить его свойства. Например, если в качестве данных выступает массив, то необходимо задать его размерность, границы индексов, тип элементов массива. Описательная часть языка программирования является необходимой как для системных программистов - разработчиков трансляторов, которые должны, в частности, проводить синтаксическую и семантическую диагностику программ, - так и для «прикладного» программиста, которому объявления программных

объектов часто облегчают процесс разработки и отладки программ.

В некоторых языках стандартные описания простых числовых и символьных данных опускают (описания по умолчанию), или в них задаются правила описания по имени объекта. Например, в Фортране переменные, имена которых начинаются с букв I, J, К, L, M, N, могут принимать целые значения (при отсутствии явного описания типа, которое возможно), т.е. определены как числовые данные целого типа. В Бейсике-MSX данные строкового типа присваиваются переменным, имена которых заканчиваются специальным символом $: A$, S1$.

Особый интерес представляют в языках программирования описания нестандартных структур данных, таких как запись, файл, объект, список, дерево и т.п.

Приведем список наиболее употребительных обозначений типов данных, используемых в описаниях:

Целый                        - Integer

Вещественный         - Real



Логический                - Boolean

Символьный              - Char

Строковый               - String

Массив                       - Array

Множество              -Set

Файл                          - File

Запись                                    - Record

Объект                      - Object

 

Переменные играют важнейшую роль в системах программирования. Понятие «переменная» в языках программирования отличается от общепринятого в математике. Переменная - это программный объект, способный принимать некоторое значение с помощью оператора присваивания. В ходе выполнения программы значения переменной могут неоднократно изменяться. Каждая переменная после ее описания отождествляется с некоторой ячейкой памяти, содержимое которой является ее значением. Синтаксис переменной, точнее, ее идентификатора, как правило, имеет вид:

<имя переменной>::=

——><буква>———>

—><буква>———>

—><цифра>——>

—><спецсимвол>

Семантический смысл переменной заключается в хранении некоторого значения. соответствующего ее типу (например, переменная целого типа может принимать значение произвольного целого числа), а также в выполнении с ней операций пересылки в нее и извлечения из нее этого значения.

Функция - это программный объект, задающий вычислительную процедуру определения значения, зависимого от некоторых аргументов. Вводится в языки программирования для задания программистом необходимых ему функциональных зависимостей. В каждом языке высокого уровня имеется в наличии библиотека стандартных функций: арифметических, логических, символьных, файловых и т.п. Функции -стандартные и задаваемые программистом - используются в программе в выражениях.

Выражения строятся из величин - постоянных и переменных, функций, скобок. знаков операций и т.д. Выражение имеет определенный тип, определяемый типом принимаемых в итоге его вычисления значений. Возможны выражения арифметические, принимающие числовые значения, логические, символьные, строковые и т.д.


Выражение 5+ 7 является, несомненно, арифметическим, выражение А + В может иметь cамый разный смысл - в зависимости от того, что стоит за идентификаторами А и В.

Процедура - это программный объект, представляющий некоторый самостоятельный этап обработки данных. По сути, процедуры явились преемниками подпрограмм, которые были введены для облегчения разработки программ еще на самых ранних стадиях формирования алгоритмических языков. Процедура имеет входные и выходные параметры, называемые формальными. При использовании процедуры формальные параметры заменяются на фактические.

Модуль (Unit) - это специальная программная единица, предназначенная для создания библиотек и разделения больших программ на логически связанные блоки.

По сути, модуль - это набор констант, типов данных, переменных, процедур и функций. В состав модуля входят разделы: заголовок, интерфейс, реализация, инициализация.

Заголовок

необходим для ссылок на модуль.

Интерфейс содержит объявления, включая процедуры и функции.

Раздел «реализация»

содержит тела процедур и функций, перечисленных в интерфейсной части.

Раздел «инициализация» содержит операторы, необходимые для инициализации модуля.

Каждый модуль компилируется отдельно, и каждый элемент модуля можно использовать в программе без дополнительного объявления.

Контрольные вопросы и задания

1. Какие преимущества имеют языки программирования высокого уровня по сравнению с машинно-ориентированными языками?

2. Каковы основные составляющие языка программирования высокого уровня?

3. В чем различия понятий языков программирования от аналогичных понятий математического «языка»?

4. С какой целью используются и что представляют собой металингвистические формулы Бэкуса-Наура?

5. Что представляет собой синтаксическая диаграмма Вирта?

6. В чем различие между постоянными и переменными величинами? Чем характеризуется величина?

7. В чем принципиальная разница между величинами простыми и структурированными?

8. Для чего служит описание величин в программах?

9. В чем состоит назначение функций? процедур? модулей?

И НЕ ТОЛЬКО ПЕРСОНАЛЬНЫЕ КОМПЬЮТЕРЫ...

Массовость использования ПК, огромные рекламные усилия производителей и коммерсантов не должны заслонить тот факт, что кроме ПК есть и другие, многократно более мощные, вычислительные системы Всегда есть круг задач, для которых недостаточно существующих вычислительных мощностей и которые столь важны, что для их решения не жалко никаких средств. Это, например, может быть связано с обороноспособностью государства, решением сложнейших научно-технических задач, созданием и поддержкой гигантских банков данных. В настоящее время лишь немногие государства способны производить, так называемые, супер-ЭВМ - компьютеры, на фоне которых «персоналки» кажутся игрушками. Впрочем, сегодня ПК часто становится терминалом - конечным звеном в гигантских телекоммуникационных системах, в которых решением непосильных для ПК задач обработки информации занимрются более мощные ЭВМ.

Схема классификации компьютеров, исходящая из их производительности, размеров и функционального назначения, приведена на рис. 4.9. Следует отметить, что вопрос об отнесении конкретного компьютера к одной из категорий этой схемы может иметь неоднозначный ответ, привязанный к конкретной исторической обстановке или доминирующему поколению ЭВМ.

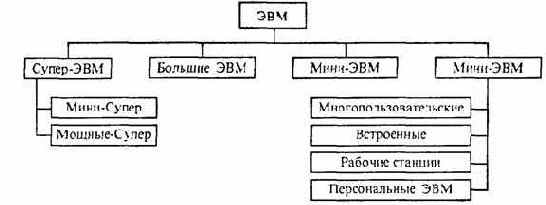
Рис. 4.9.

Классификация ЭВМ

Место супер-ЭВМ в этой иерархии уже обсуждалось. Определить супер-ЭВМ можно лишь относительно: это самая мощная вычислительная система, существующая в соответствующий исторический период. В настоящее время наиболее известны мощные супер-ЭВМ «Cray» и «IBM SP2» (США). Модель «Сгау-3», выпускаемая с начала 90-х годов на основе принципиально новых микроэлектронных технологий, является 16-процессорной машиной с быстродействием более 10 млрд. операций в секунду (по другим данным 16) над числами с «плавающей точкой» (т.е. длинными десятичными числами; такие операции гораздо более трудоемки, чем над целыми числами); в модели CS 6400 число процессоров доведено до 64. Супер-ЭВМ требуют особого температурного режима, зачастую водяного охлаждения (или даже охлаждения жидким азотом).
Их производство по масштабам несопоставимо с производством компьютеров других классов (так, в 1995 г. корпорацией «Cray» было выпущено всего около 70 таких компьютеров).

Большие ЭВМ более доступны, чем «супер». Они также требуют специального помещения, иногда весьма немалого, поддержания жесткого температурного режима, высококвалифицированного обслуживания. Такую ЭВМ в 80-е годы мог себе позволить завод, даже крупный вуз. Классическим примером служат выпускавшиеся еще недавно в США машины серии IBM 370 и их отечественные аналоги ЕС ЭВМ. Большие ЭВМ используются для производства сложных научно-технических расчетов, математического моделирования, а также в качестве центральных машин в крупных автоматизированных системах управления. Впрочем, скорость прогресса в развитии вычислительной техники такова, что возможности больших ЭВМ конца 80-х годов практически по всем параметрам перекрыты наиболее мощными «супер-мини» середины 90-х. Несмотря на это, выпуск больших машин продолжается, хотя цена одной машины может составлять несколько десятков миллионов долларов.

Мини-ЭВМ появились в начале 70-х годов. Их традиционное использование -либо для управления технологическими процессами, либо в режиме разделения времени в качестве управляющей машины небольшой локальной сети. Мини-ЭВМ используются, в частности, для управления станками с ЧПУ, другим оборудованием. Среди них выделяются «супер-мини», имеющие характеристики, сравнимые с характеристиками больших машин (например, в 80-х годах таковыми считалось семейство VAX-11 фирмы DEC и его отечественные аналоги - СМ 1700 и др.).

Микро-ЭВМ обязаны своим появлением микропроцессорам. Среди них выделяют многопользовательские, оборудованные многими выносными терминалами и работающие в режиме разделения времени; встроенные, которые могут управлять станком, какой-либо подсистемой автомобиля или другого устройства (в том числе и военного назначения), будучи его малой частью. Эти встроенные устройства (их часто называют контроллерами) выполняются в виде небольших плат, не имеющих рядом привычных для пользователя компьютера внешних устройств.



Термин «рабочая станция» используется в нескольких, порой несовпадающих, смыслах. Так, рабочей станцией может быть мощная микро-ЭВМ, ориентированная на специализированные работы высокого профессионального уровня, которую нельзя отнести к персональным компьютерам хотя бы в силу очень высокой стоимости. Например, это графические рабочие станции для выполнения работ по автоматизированному проектированию или для высокоуровневой издательской деятельности. Рабочей станцией могут называть и компьютер, выполняющий роль хост-машины в подузле глобальной вычислительной сети. Компьютеры фирм «Sun Microsystems», «Hewlett-Packard», стоимостью в десятки раз большей, чем персональные компьютеры, являются одно- или многопроцессорными машинами с огромным (по меркам ПК) ОЗУ, мультипроцессорной версией операционной системы, несколькими CD ROM- накопителями и т.д.

Нельзя, наконец, не сказать несколько слов об устройствах, приносящих большую пользу и также являющихся ЭВМ (поскольку они чаще всего и электронные, и вычислительные),-аналоговых вычислительных машинах (АВМ). Они уже полвека хотя и находятся на обочине развития современной вычислительной техники, но неизменно выживают. Известны системы, в которых АВМ сопрягаются с цифровыми, значительно увеличивая эффективность решения задач в целом. Основное в АВМ - они не цифровые, обрабатывают информацию, представленную не в дискретной, а в непрерывной форме (чаще всего в форме электрических токов). Их главное достоинство - способность к математическому моделированию процессов, описываемых дифференциальными уравнениями (порой очень сложных) в реальном масштабе времени. Недостаток - относительно низкая точность получаемых решений и неуниверсальность.

И ПРОЦЕССОВ В ПРИБЛИЖЕНИИ СПЛОШНОЙ СРЕДЫ

Абстрактное понятие «сплошная среда» широчайшим образом используется в науке. Во многих ситуациях жидкости, газы, твердые тела, плазму можно рассматривать как «сплошные», отвлекаясь от их молекулярного и атомарного устройства. Например, при распространении волн в жидкости или газе реальная дискретность этих сред практически не сказывается на свойствах волн, если длина волны много больше характерного межмолекулярного расстояния; при изучении процессов распространения тепла или диффузии тоже до поры-до времени можно «забыть» об атомарном строении вещества и оперировать такими характеристиками как теплоемкость, теплопроводность, скорость диффузии и др., которые можно обсуждать и практически использовать в технике без выяснения их микроскопической природы. Вообще, «макрофизика» может быть очень полезной чисто практически без привлечения «микрофизики», которая стремится докопаться до объяснения природы явлений, исходя из атомарных и еще более «микроскопических» представлений.

В приближении сплошной среды свойства объекта описываются математически с помощью непрерывных функций от координат и времени: f(

,t)). За каждым «свойством» закрепляется такая функция, и их взаимосвязаный вид дает полное описание среды.

Существующие задачи можно разделить на два класса: статические и динамические. В первом случае значения величин, характеризующих сплошную среду, не зависят от времени, и требуется найти их пространственное распределение. Хорошо известные примеры: как распределено в пространстве значение электрического поля, созданного неподвижным точечным зарядом? как распределены электрическое поле в конденсаторе? поле постоянного магнита? скорости в стационарно движущемся по трубе потоке жидкости? На рис. 7.24 дан (схематически) ответ на последний вопрос: чем ближе к стенке трубы, тем меньше скорость из-за естественной вязкости жидкости и трения о стенку трубы. Качественно понять указанную закономерность можно, вероятно, без всяких уравнений, но определить профиль скоростей, т.е.
форму огибающей векторов скорости без математического моделирования невозможно. Таких задач, представляющих огромный практический интерес, очень много, а связанные с их решением математические проблемы столь сложны, что чаще всего соответствующее математическое моделирование может быть реализовано лишь на компьютере.

Рис. 7.24. Распределение скоростей в потоке жидкости, движущейся в трубе

Как правило, еще сложнее решение динамических задач. Если электрическое поле создается движущимися зарядами, то определить, как оно меняется во времени в каждой точке пространства - задача очень непростая. Не менее трудно определить эволюцию скорости в разных местах в жидкости, если в некотором месте пульсирует давление; изменения значений температуры в разных точках некоторого тела, которое подогревают изнутри или извне от источников тепла, интенсивность которых изменяется со временем.

Подобные задачи привлекают неослабевающее внимание физиков, научных работников смежных областей, инженеров уже не менее 200 лет. Практическая необходимость в их решении велика; без этого не спроектировать ни современных технических устройств и механизмов, ни строений, ни космических аппаратов, ни многого другого. Главный способ решения таких задач - математическое моделирование. Любопытно, что и сами компьютеры, и входящие в них микроэлементы невозможно спроектировать без оценок электрических полей и потоков тепла от этих устройств.

Поскольку математический аппарат такого моделирования бывает весьма сложен, мы ограничимся лишь двумя относительно простыми задачами, в которых отражается часть общих закономерностей. Одна из них - статическая, другая -динамическая.

Распределение электростатического поля. Что стоит за электрической (кулоновской) силой, заставляющей двигаться заряженную частицу q? – Ответ хорошо известен: электрическое поле , существующее в каждой точке пространства, созданное другими заряженными телами (которые будем считать неподвижными). Если это поле создается одним точечным зарядом Q, то величина напряженности поля зависит от расстояния r



от Q до данной точки пространства: , ее направление - по радиусу от заряда (если Q положителен). Поле это существует совершенно независимо от «пробного» заряда q и может рассматриваться как сплошная среда. Существуют две взаимосвязаные характеристики электрического поля: напряженность E (векторная характеристика) и потенциал ? - скалярная. Для поля точечного заряда .

Если поле создано не одним, а несколькими зарядами, то напряженность и потенциал в каждой точке можно найти из известного принципа суперпозиции:



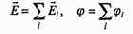
где  и ?i создаются в этой точке i-м зарядом, рис. 7.25. По отношению к  принцип суперпозиции означает необходимость векторного сложения, к ? — «обычного» (с учетом знаков отдельных потенциалов).

Зная потенциал в каждой точке поля, т.е. функцию Ф = ? (х, у, z), можно найти напряженность в каждой точке чисто математическим путем, отражающим тот факт, что проекция вектора напряженности на любое направление есть скорость изменения потенциала в этом направлении:

(7.43)



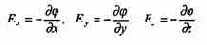
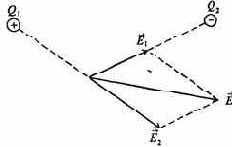
Рис. 7.25. Нахождение напряженности электрического поля по принципу суперпозиции

Частным случаем (7.43) являются формулы  и  для одного точечного заряда. Действительно, фиксируем некоторую точку А

поля на расстоянии r от заряда Q и введем локальную систему координат с центром в А; у этой системы ось r является продолжением радиуса-вектора r, а две другие оси –х и у -

перпендикулярны к ней. Примем, что , и найдем ,

опираясь на формулы (7.43). Поскольку ?A от х и у

не зависит, то  =

0,  = 0, а



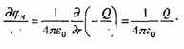
таким образом,  - т.е. мы пришли к известному результату о величине и направлении поля, созданного точечным зарядом.

Расчет электрического поля - важная в прикладном плане задача. В реальных конструкциях поле создается не одним-двумя точечными зарядами, а достаточно причудливо расположенными в пространстве заряженными телами самых разнообразных форм: пластины, плоские и изогнутые; штыри; правильные и деформированные сфероиды и т.д. Для инженера и научного работника важно иметь наглядную картину поля, изображенного некоторым условным образом.


Самое неудобное изображение, почти не используемое - нарисовать много стрелок, соответствующих напряженности поля в разных точках, так, чтобы длины стрелок были пропорциональны напряженностям. Такой рисунок является громоздким, стрелки на нем пересекаются, мелкие детали выявить трудно. Есть два классических способа для наглядного изображения поля: поверхностями (или линиями) равного потенциала и силовыми линиями поля.

Можно доказать, что для любого электростатического поля множество точек, потенциал в которых одинаков, т.е. точек, удовлетворяющих уравнению ? (х, у, г) = ?0, при любом ?0 образует замкнутую поверхность (так называемую, эквипотенциальную поверхность). Для одного точечного заряда это сфера; в общем случае эта поверхность может быть очень сложной. Для многих технических приложений знать форму таких поверхностей просто необходимо - например, чтобы, располагая детали конструкции, избежать между ними большой разности потенциалов. Линии равного потенциала являются сечениями поверхности равного потенциала той плоскостью, в которой строится изображение.

Силовые линии, как известно из любого учебника физики, есть такие линии, касательные к которым в каждой точке задают направление вектора напряженности поля. Силовые линии никогда не пересекаются между собой. Они начинаются на положительных зарядах и либо заканчиваются на отрицательных, либо уходят «на бесконечность». По обычному соглашению число силовых линий, исходящих из точечного заряда, пропорционально величине этого заряда; коэффициент пропорциональности выбирается таким, чтобы изображение было легко читаемым.

Обсудим практический метод построения картины поверхностей равного потенциала для системы, состоящей из нескольких точечных зарядов произвольной величины и знака, любым способом расположенных в пространстве. Введем некоторую систему координат, начало которой удобнее расположить в «пустой» точке, т.е. ни на одном из зарядов. Пусть в этой системе координаты зарядов имеют значения  = (хj,уj,zj), j= 1,2,...р, где р - число зарядов.



Поскольку изображать трехмерные поверхности - дело достаточно сложное, рассмотрим вначале построение линий равного потенциала (изолиний), образованных сечением поверхности равного потенциала некоторой плоскостью; пусть, для определенности, это будет плоскость л'}'. Воспользуемся методом сеток, играющим в моделировании свойств сплошных сред исключительно важную роль.

Выберем по осям х

и у некоторые шаги hx

и hy и покроем плоскость сеткой, образованной прямыми, параллельными осям х

и у и отстоящими друг от друга на расстояниях hx

и hy

соответственно. Точки пересечения этих прямых — узлы сетки. Пронумеруем их так: начало координат (0, 0), следующий по оси x вправо - (0, 1), влево - (0, -1); по оси у вверх - (1, 0), вниз (-1, 0) и т.д. Значения потенциала, создаваемого системой зарядов Q1 … Qp

в узле (i ,k), согласно принципу суперпозиции, таково (обратим внимание, что здесь и ниже i

- номер строки, k -

столбца сетки):



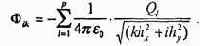
Ограничимся прямоугольной областью в плоскости ху: [-mhx, mhx] по оси х

и [-nhy, nhy] по оси у. В этой области (2m + l) • (2n + l) узлов. Вычислим значения потенциала в каждом из них по указанным формулам; для ЭВМ эта задача совершенно элементарна, даже если т и n составляют несколько десятков или сотен. В результате получим матрицу значений потенциала.

Фиксируем некоторое значение потенциала Ф и построим изолинию, соответствующую этому значению. Для этого проходим, к примеру, по i-ой горизонтальной линии сетки и ищем среди ее узлов такие соседние, значения потенциала в которых «захватывают» Ф между собой; признаком этого может служить выполнение неравенства



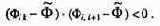
Если такая пара узлов найдена, то координату точки, в которой Ф = Ф , найдем приближенно с помощью линейной интерполяции:

(7.44)

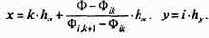
Найдя в данной горизонтали все такие точки, переходим к следующей горизонтали, пока не исчерпаем их все. Для этого надо совершить двойной циклический проход: во внешнем цикле перебирать i от -п до +п, во

внутреннем перебирать k

от - т до +т.

После этого следует аналогично заняться поиском нужных точек на вертикальных линиях сетки.


Детали процедуры очевидны; формулы, аналогичные (7.44), имеют вид:

(7.45)

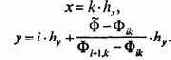
После прохождения всех горизонтальных и вертикальных линий сетки находятся все те точки на этих линиях, в которых потенциал равен . Проведя — мысленно или на бумаге — кривую, плавно проходящую через ближайшие точки, получаем искомую изолинию (разумеется лишь в том случае, если значение  выбрано разумно и такая линия есть в пределах рассматриваемой области). Затем берем другие значения  и повторяем указанную процедуру, получая таким образом семейство изолиний.

Приведенная ниже программа реализует указанные построения. Предполагается, что все заряды лежат в одной плоскости, и изолинии строятся тоже лишь в этой плоскости.

Программа 149.

Программа построения линий равного потенциала.

Program Potential;

Uses Crt, Graph;

Const N = 100; (Размер сетки NxN}

Var X, У, Q, G : Array[1..10] Of Real; F : Array[0..N, 0..N] Of Real;

    I, J, M, L, K: Integer; A, B, R: Real;

Begin

 WriteLn('Сколько зарядов? (не более 10)'); ReadLn(K);

 Write('Ведите координаты x, у и величины зарядов q');

 WriteLn('(координаты - в диапазоне 0-1)');

 For I := 1 То К Do

Begin Write('х[', I, ']=');

ReadLn(X[I]); Write('y[', I, ']='); ReadLn(Y(I]);

Write('q[', I, ']= '); ReadLn(Q[I])

  End;

For I := 0 To N Do

For J := 0 To N Do

For M := 1 To K Do

Begin

R := Sqrt(Sqr(I / N - X[M]) + Sqr(J / N - Y[M]));

  If R>=1E-6 Then F(I,J]:= F(I,J]+Q[M]/R Else F[I,J]:=1E+8

       End;

Write('Сколько построить изолиний? (не более 10)'); ReadLn(L);

WriteLn('Введите значения потенциала g для построения изолиний');

For I := 1 То L Do

Begin Write ('g[', I, ']='); ReadLn(G(I]) End;

DetectGraph(I, J); InitGraph(I, J, ");

For I := 1 To К Do

Begin

A := X[I] * GetMaxX; В := (1 - Y[I]) * GetMaxY;

Circle(Round(A), Round(B), 4); FloodFill(Round(A), Round(B),

GetColor) ;

End;

For M := 1 To L Do

Begin

B := G[M]; SetColor(M);

For I := 0 To N Do

For J := 0 To N - 1 Do

If (F[I, J] - B) * (F[I, J + 1] - В) < О



Then Begin

A:=(J+(B-F[I,J])/(F[I,J+1]-F[I,J]))/N;

Circle(Round;I/N*GetMaxX), Round((1-A)*GetMaxY), 1)

     End;

For J := 0 To N Do

For I := 0 To N - 1 Do

If (F[I, J] - B) * (F[I + 1, J] - В) < 0 Then Begin

A:=(I+(B-F[I,J])/(F[I+1,J]-F[I,J]))/N;

Circle(Round(A*GetMaxX), Round((1-J/N)*GetMaxY), 1)

                       End

                  End;

SetColor(15); OutTextXY(10, 50, 'для продолжения нажмите любую клавишу');

Repeat Until KeyPressed; CloseGraph;

End.

Несколько примеров использования этой программы приведены на рис. 7.26, 7.27.



Рис. 7.26. Поле создано семью зарядами q1 = q2 = q3 = q4

= 1, q5

= q6

= q7 = -1,

имеющими соответственно координаты (0,2;0,2), (0,8;0,8), (0,2;0,8), (0,8;0,2), (0,2;0,5), (0,5;0,5), (0,8;0,5). Изолинии построены для потенциалов -4, -3, -2, -1,0, 1, 2, 3,4



Рис. 7.27. Поле создано пятью зарядами q1 = 1, q2 = -2, q3 = 2, q4 = -3, q5 = 1, имеющими соответственно координаты (0,3; 0,75), (0,2; 0,5), (0,7; 0,2), (0,5; 0,9), (0,5; 0,5). Изолинии построены для потенциалов -4, -3, -2, -1,0, 1, 2, 3,4

Оставим технические вопросы на самостоятельное решение и обсудим некоторые принципиальные. Допустим, между двумя ближайшими узлами выполняется записанное выше неравенство - означает ли это, что между ними действительно лежит одна

точка, в которой Ф = ? Ответить нетрудно: да, если потенциал между этими узлами меняется монотонно. Если же узлы столь редки (т.е. hx

и (или) hy

слишком велики), что потенциал между соседними узлами меняется немонотонно, то числа, полученные по формулам (6.44), (6.45), не имеют практически никакого отношения к реальным точкам, в которых Ф = ; это утверждение проиллюстрировано рис. 7.28.

Очевидно, что для получения изолиний следует брать достаточно малые hx

и hy. Проверка достоверности (эмпирическая) состоит в том, что строится картина изолиний с некоторыми hx и hy (часто берут hx = hy), а затем с вдвое меньшими значениями; если картины близки, то построение на этом завершается.



Даже если все заряды лежат в одной плоскости (как это было на рис. 7.26 и 7.27), поле существует, конечно, и вне этой плоскости. Один из способов наглядного построения изображения поля - найти изолинии, соответствующие некоторому фиксированному набору значений Ф; в нескольких параллельных плоскостях и представить их на общем рисунке, дающем представление о поверхностях равного потенциала. Для этого программу, приведенную выше, следует слегка дополнить.

Метод сеток в разных задачах физики сплошных сред принимает разное обличие; еще один пример впереди. Однако, во всех случаях за ним скрыта общая идея, обладающая большой познавательной силой - идея дискретизации, т.е. представления непрерывной величины, имеющей бесконечно много значений, отдельными порциями, описываемыми конечным набором значений. Эта идея продуктивна не только в физике, но и в прикладной математике, информатике, других науках.



Рис. 7.28 На верхнем рисунке ? - точка, в которой Ф = Ф0. ? ? ? - найдено линейной интерполяцией. На нижнем рисунке точек, в которых Ф = Ф0, много; ? формально найдено линейной интерполяцией

Для построения силовых линии поля можно поступить следующим образом. Выберем некоторую точку с координатами (?0, ?0, ?0) и найдем в ней напряженность поля



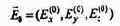
по правилу суперпозиции

(7.46)

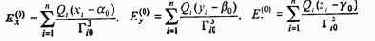
где



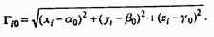
Проведем мысленно в точке (?0, ?0, ?0) касательную к  и возьмем вдоль нее небольшой отрезок длины h, начинающийся в  ; координаты конца отрезка

(7.47)

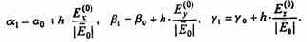
Тем самым получаем координаты точки А', лежащей на касательной к силовой линии (вместо точки А, лежащей на самой линии) Если h

мало, то А' близко к А. Далее, отправляясь от А', найдем по той же схеме следующую точку В' вблизи силовой линии и т.д. Ломаная OA'B''... приблизительно передает силовую линию. Построение целесообразно начать вблизи какого-нибудь положительного заряда (если он есть) и закончить тогда, когда силовая линия подойдет вплотную к отрицательному заряду или уйдет «на бесконечность».

Построение картины силовых линий, дающих представление о поле - дело неформальное, требующее понимания физической сущности.Два семейства взаимно перпендикулярных линий - равного потенциала и силовых - дают весьма наглядную и исчерпывающую характеристику электростатического поля.

Учитывая трудности визуализации трехмерных изображений, целесообразно ограничиться (по крайней мере вначале) рассмотрением ситуаций, когда все заряды лежат в одной плоскости; тогда силовая линия, начинающаяся из любой точки данной плоскости, из этой плоскости не выйдет, и получится легко воспринимаемая картина.

Способ получения формул (7.47) есть частный случай приема линеаризации -сведения сложной зависимости к простейшей линейной для малых расстояний (или времен). Это мощнейший прием в моделировании физических процессов и в построении многих методов численного анализа. Фактически он лежит в основе дифференциального исчисления - само понятие производной возникает при линеаризации функции.

---

---