СХЕМНАЯ РЕАЛИЗАЦИЯ ЭЛЕМЕНТАРНЫХ ЛОГИЧЕСКИХ ОПЕРАЦИЙ. ТИПОВЫЕ ЛОГИЧЕСКИЕ УЗЛЫ
Мы уже знаем, что любую достаточно сложную логическую функцию можно реализовать, имея относительно простой набор базовых логических операций. Первоначально этот тезис был технически реализован «один к одному»: были разработаны и выпускались микросхемы, соответствующие основным логическим действиям. Потребитель, комбинируя имеющиеся в его распоряжении элементы, мог получить схему с реализацией необходимой логики. Довольно быстро стало ясно, что подобное «строительство здания из отдельных кирпичиков» не может удовлетворить практические потребности. Промышленность увеличила степень интеграции МС и начала выпускать более сложные типовые узлы: триггеры, регистры, счетчики, дешифраторы, сумматоры и т.д. (продолжая аналогию со строительством, этот шаг, видимо, следует уподобить панельному способу домостроения). Новые микросхемы давали возможность реализовывать еще более сложные электронные логические устройства, но человеку свойственно не останавливаться на достигнутом: рост возможностей порождает новые потребности. Последовал переход к большим интегральным схемам (БИС), представлявшим из себя функционально законченные узлы, а не отдельные компоненты для их создания (как тут не вспомнить блочный метод постройки здания из готовых комнат). Наконец, дальнейшая эволюция технологий производства ИМС привела к настолько высокой степени интеграции, что в одной БИС содержалось функционально законченное изделие: часы, калькулятор, небольшая специализированная ЭВМ...
Если посмотреть на внутреннее устройство типичного современного компьютера, то там присутствуют ИМС очень высокого уровня интеграции: микропроцессор, модули ОЗУ, контроллеры внешних устройств и др. Фактически каждая микросхема или небольшая группа микросхем образуют функционально законченный блок. Уровень сложности блока таков, что разобраться в его внутреннем устройстве для неспециалиста не только нецелесообразно, а просто невозможно. К счастью, для понимания внутренних принципов работы современной ЭВМ достаточно рассмотреть несколько типовых узлов, а изучение поведения БИС заменить изучением функциональной схемы компьютера.
Обработка информации в ЭВМ происходит, как уже не раз отмечалось выше, путем последовательного выполнения элементарных операций. Эти операции менее многочисленны, нежели набор команд ЭВМ (которые реализуются через цепочки этих операций). К элементарным операциям относятся: установка - запись в операционный элемент (например, регистр) двоичного кода; прием - передача (перезапись) кода из одного элемента в другой; сдвиг - изменение положения кода относительно исходного; преобразование - перекодирование; сложение - арифметическое сложение целых двоичных чисел - и некоторые другие. Для выполнения каждой из этих операций сконструированы электронные узлы. являющиеся основными узлами цифровых вычислительных машин - регистры, счетчики, сумматоры, преобразователи кодов и т.д.
В основе каждой из элементарных операций лежит некоторая последовательность логических действий, описанных в предыдущем параграфе. Проанализируем, например, операцию сложения двух чисел: 3+6. Имеем:
011
+ 110
1011
На каждом элементарнейшем шаге этой деятельности двум двоичным цифрам сопоставляется двоичное число (одно- или двузначное) по правилам: (0,0) => О, (0,1) => 1, (1.0) =>
1, (1,1) => 10. Таким образом, сложение цифр можно описать логической бинарной функцией. Если дополнить это логическим правилом переноса единицы в старший разряд (оно будет сформулировано ниже при описании работы сумматора), то сложение полностью сведется к цепочке логических операций.
Для дальнейшего рассмотрения необходимо знать условные обозначения базовых логических элементов. Они приведены на рис. 4.21. Соответствующие таблицы истинности приведены в предыдущем пункте.
Отметим, что на практике логические элементы могут иметь не один или два, а значительно большее число входов.
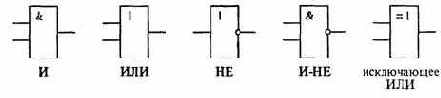
Рис. 4.21. Условные обозначения основных логических элементов
Итак, примем к сведению, что простейшие логические элементы, изображенные на рис. 4.21, можно реализовать аппаратно. Это означает, что можно создать электронные устройства на транзисторах, резисторах и т.п., каждое из которых имеет один или два входа для подачи управляющих напряжений и один выход, напряжение на котором определяется соответствующей таблицей истинности.
На практике логическому «да» («истина», или цифра 1 в таблицах истинности) соответствует наличие напряжения, логическому «нет» («ложь», или цифра 0) - его отсутствие.
Вопрос, на который мы должны ответить, таков: как с помощью таких элементарных схем реализовать сложные цифровые устройства, необходимые для работы ЭВМ? При этом, учитывая существование прямых соответствий между логическими и электронными схемами, вполне достаточно достичь понимания на уровне логических схем.
В качестве характерных устройств выберем два наиболее важных и интересных -триггер (рис. 4.22) и сумматор. Первый - основа устройств оперативного хранения информации, второй служит для сложения чисел.
Перейдем к описанию работы триггера. Соответствующая его работе таблица истинности (табл. 4.7) приведена ниже.
Как видно из рис. 4.22, простейший вариант триггера собирается из четырех логических элементов И-НЕ, причем два из них играют вспомогательную роль. Триггер имеет два входа, обозначенные на схеме R и S, а также два выхода, помеченные буквой Q - прямой и инверсный (черта над Q у инверсного выхода означает отрицание). Триггер устроен таким образом, что на прямом и инверсном выходах сигналы всегда противоположны.
Как же работает триггер? Пусть на входе R установлена 1, а на S - 0. Логические элементы D1 и D2 инвертируют эти сигналы, т.е. меняют их значения на противоположные. В результате на вход элемента D3 поступает 1, а на D4 - 0. Поскольку на одном из входов D4 есть 0. независимо от состояния другого входа на его выходе (он же является инверсным выходом триггера!) обязательно установится 1. Эта единица передается на вход элемента D3 и в сочетании с 1 на другом входе порождает на выходе D3 логический 0. Итак, при R=1 и S=0 на прямом выходе триггера устанавливается 0, а на инверсном - 1.
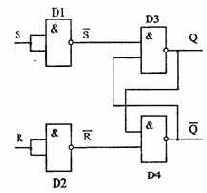
Рис. 4.22. Логическая схема триггера
Таблица 4.7
Таблица истинности RS-тригтера
|
S |
R |
 |
 |
Q |
 |
Примечания |
|
0 0 1 1 |
0 1 0 1 |
1 1 0 0 |
1 0 1 0 |
X 0 1 (1 |
X 1 0 1) |
Хранение Запрещено |
Обозначение состояния триггера по договоренности связывается с прямым выходом. Тогда при описанной выше комбинации входных сигналов результирующее состояние можно условно назвать нулевым: говорят, что триггер «устанавливается в 0» или «сбрасывается». Сброс по-английски называется «Reset», отсюда вход, появление сигнала на котором приводит к сбросу триггера, обычно обозначают буквой R.
Проведите аналогичные рассуждения для «симметричного» случая R =0 и S = 1. Вы увидите, что на прямом выходе получится логическая 1, а на инверсном - 0. Триггер перейдет в единичное состояние - «установится» (установка по-английски - «Set»).
Теперь рассмотрим наиболее распространенную и интересную ситуацию R = 0 и S = 0 - входных сигналов нет. Тогда на входы элементов D3 и D4. связанные с R и S будет подана и их выходной сигнал будет зависеть от сигналов на противопо-ложных входах. Нетрудно убедится, что такое состояние будет устойчивым. Пусть, например, на прямом выходе 1. Тогда наличие единиц на обоих входах элемента D4 «подтверждает» нулевой сигнал на его выходе. В свою очередь, наличие 0 на инверсном выходе передается на D3 и поддерживает его выходное единичное состояние. Аналогично доказывается устойчивость картины и для противоположного состояния триггера, когда Q = 0.
Таким образом, при отсутствии входных сигналов триггер сохраняет свое «предыдущее» состояние. Иными словами, если на вход R подать 1, а затем убрать, триггер установится в нулевое состояние и будет его сохранять, пока не поступит сигнал на другой вход S. В последнем случае он перебросится в единичное состояние и после прекращения действия входного сигнала будет сохранять на прямом выходе 1. Мы видим, что триггер обладает замечательным свойством: после снятия входных сигналов он сохраняет свое состояние, а значит может служить устройством для хранения одного бита информации.
В заключение проанализируем последнюю комбинацию входных сигналов: R = 1 и S = 1. Нетрудно убедиться (проделайте необходимые рассуждения самостоятельно), что в этом случае на обоих выходах триггера установится I! Такое состояние помимо своей логической абсурдности еще и является неустойчивым: после снятия входных сигналов триггер случайным образом перейдет в одно из своих устойчивых состояний.
Вследствие этого, комбинация R = 1 и S = 1 никогда не используется на практике и является запрещенной.
Мы рассмотрели простейший RS-триггер. Существуют и другие разновидности этого интересного и полезного устройства. Все они различаются не столько принципом работы, сколько входной логикой, усложняющей «поведение» триггера.
Триггеры очень широко применяются в вычислительной технике. На их основе изготовляются всевозможные регистры для хранения и некоторых видов обработки (например, сдвига) двоичной информации, счетчики импульсов и даже интегральные микросхемы статического ОЗУ, не требующие для сохранения информации специальных процессов регенерации. Множество триггеров входят в состав любого микропроцессора.
В качестве второго примера применения логических элементов в вычислительной технике рассмотрим устройство, называемое сумматором. Его назначение состоит в нахождении суммы двух двоичных чисел. Этот узел интересен для нас тем, что он лежит в основе арифметического устройства ЭВМ и иллюстрирует некоторые принципы выполнения вычислительных операций в компьютере.
Для простоты начнем с изучения логической структуры простейшего возможного устройства, являющегося звеном сумматора. Это устройство - полусумматор - реализует сложение двух одноразрядных двоичных, чисел, которые обозначим А и В. В результате получается, вообще говоря, двухразрядное двоичное число. Его младшую цифру обозначим S, а старшую, которая при сложении многоразрядных чисел будет перенесена в старший разряд, через Со (от английских слов «Carry out»- «выходной перенос»). Для лучшего понимания происходящего вспомните правило типа «ноль пишем, один в уме».
Обе цифры можно получить по следующим логическим формулам:

(черта над символом обозначает операцию NOT, знак ^ - конъюнкцию, знак v -дизъюнкцию). Это легко проверить перебором всех четырех возможных случаев сочетания значений А и В, пользуясь табл. 4.5 и табл. 4.8.
Таблица 4.8
Таблица истинности для полусумматора
|
А |
В |
S |
Со |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
Мысленно объединим в табл. 4.8 столбцы А, В и Со. Полученная таблица напоминает базовый логический элемент И. Аналогично, сравнив первые три столбца А.В и S с имеющимися в предыдущем разделе таблицами истинности для распространенных логических элементов, обнаружим подходящий для наших целей элемент «исключающее ИЛИ». Таким образом, для реализации полусумматора достаточно соединить параллельно входы двух логических элементов (рис. 4.23).
Ниже приведены два варианта логической схемы полусумматора: с использованием лишь базовых логических элементов и с использованием логического элемента «исключающее ИЛИ». Видно, что вторая схема существенно проще.
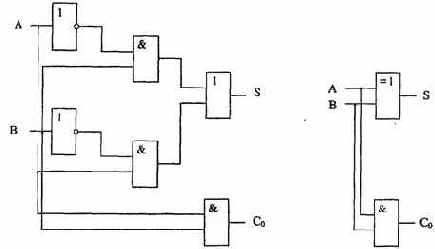
Рис. 4.23. Логическая схема полусумматора (два варианта)
Полный одноразрядный сумматор «умеет» при сложении двух цифр учитывать возможное наличие единицы, переносимой из старшего разряда (той, которая при обычном сложении столбиком остается «в уме»). Обозначим этот «бит переноса» через Ci (от английского «Carry in» - «входной перенос»).
Таблица 4.9
Таблица истинности для полусумматора
|
Входы |
Выходы |
||||
|
А |
В |
Ci |
S |
Со |
|
|
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
1 |
1 |
0 |
|
|
0 |
1 |
1 |
1 |
0 |
|
|
0 1 |
1 0 |
0 |
0 |
1 |
|
|
1 |
1 |
0 |
|||
|
1 |
0 |
0 |
0 |
1 |
|
|
1 1 |
1 |
0 |
0 |
1 |
|
|
1 |
1 |
1 |
1 |
||
Заметим, что для суммирования младших разрядов чисел полусумматора уже достаточно, так как в этом случае отсутствует сигнал входного переноса.
Соединив два полусумматора как показано на рис. 4.24, получим полный сумматор, способный осуществить сложение двух двоичных разрядов с учетом возможности переноса.
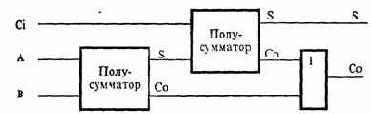
Рис. 4.24. Сумматор, составленный из двух полусумматоров
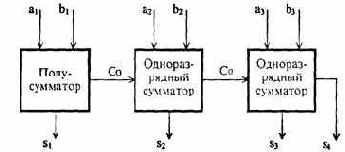
Рис. 4.25. Логическая схема суммирования двух трехразрядных двоичных чисел
Перейти к многоразрядным числам можно путем последовательного соединения соответствующего количества сумматоров. На рис. 4.25 представлена схема суммировання двух трехразрядных двоичных чисел А + В = S; в поразрядной записи эта-операция имеет следующие обозначения:
(a3a2a1) + (b3b2b1) = (S4S3S2S1)
Последовательность логических схем на рис. 4.23 - 4.25 отражает важнейшую в современной цифровой электронике и вычислительной технике идею последовательной интеграции. Такая интеграция позволяет реализовать все более функционально сложные узлы современного компьютера.
СИ И ПАСКАЛЬ
При знакомстве с языком Си, особенно после изучения Паскаля и Бейсика, погружение в детали его изобразительных средств может затушевать важную мысль: хотя на Си можно написать практически любую прикладную программу, он изначально для этого не предназначен. Си является результатом эволюционного развития языков создания системных программных средств. Если в прикладном программировании эволюция шла от Фортрана к Алголу, Коболу, Паскалю и т.д., то в системном - от Ассемблеров, привязанных к архитектуре ЭВМ, к Си, для которого созданы трансляторы, делающие его хоть и независимым от архитектуры, но не меняющим основного предназначения.
С помощью Си можно сделать то, что на Паскале сделать невозможно (или почти невозможно) - например, написать фрагмент операционной системы (или новую операционную систему), утилиты и т.п. Так, ряд трансляторов с Паскаля написаны на Си; обратное невозможно представить. В то же время, не раз отмечалось, что прикладные программы, написанные на Паскале, отличаются большей надежностью, чем написанные на Си; их легче читать, передавать от одного программиста другому для совершенствования и сопровождения. Это связано с тем, что Паскаль содержит существенно больше ограничений и является языком более высокого уровня с сильной типизацией данных. Для языка же. который предназначен для разработки системного программного обеспечения, чем меньше ограничений, тем лучше; так, в Си возможны неявные преобразования всех базовых типов данных и указателей друг в друга, что крайне желательно при создании системных средств, но при невнимательности программиста приводит к ошибкам, не улавливаемым транслятором с Си (Паскаль же подобные недопустимые операции пресекает немедленно).
Разумеется, сказанное выше не следует абсолютизировать. Программисты, привыкшие к Си, успешно пишут на нем программы различных классов. Это касается не только Си - вспомните об экспертных системах, написанных на Бейсике. В то же время, при массовом программировании придерживаться «разделения труда» между языками представляется более естественным.
Контрольные вопросы и задания
1. Охарактеризуйте назначение и особенности языка Си.
2. Какие символы образуют алфавит языка Си?
3. Что называется лексемами, идентификаторами, литералами? Приведите примеры.
4. Какие типы данных используются в Си? Приведите примеры описания переменных.
5. Охарактеризуйте арифметические, логические и битовые операции Си.
6. Какие разновидности оператора присваивания имеются в Си?
7. Как на языке Си можно описать ветвление?
8. Охарактеризуйте возможности цикла for. Приведите примеры.
9. Какие логические циклы имеются в Си? Приведите примеры их использования.
10. Какие операторы управления имеются в Си?
11. Какова структура программы на Си? Что такое функция?
12. Приведите примеры использования функций (с аргументами и без, возвращающих и не возвращающих значения).
13. Для чего в качестве аргументов функций используются указатели? Приведите примеры.
14. Для чего в Си существуют классы памяти?
15. Что такое потоки и файлы в Си?
16. Охарактеризуйте стандартные функции ввода и вывода в Си.
17. Что такое препроцессор Си? Приведите примеры директив препроцессора.
СИМПЛЕКС-МЕТОД
Для решения ряда задач линейного программирования существуют специальные методы. Есть, однако, общий метод решения всех таких задач. Он носит название симплекс-метода и состоит из алгоритма отыскания какого-нибудь произвольного допустимого решения и алгоритма последовательного перехода от этого решения к новому допустимому решению, для которого функция f изменяется в нужном направлении (для получения оптимального решения).
Пусть система ограничений состоит лишь из уравнений
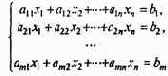
и требуется отыскать минимум линейной функции (7.81). Для отыскания произвольного опорного решения приведем (7.85) к виду, в котором некоторые r неизвестных выражены через остальные, а свободные члены неотрицательны (как это сделать - обсудим позднее):
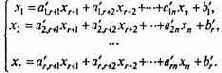
Неизвестные x1, x2, ..., xr - базисные неизвестные, набор {x1, x2, ..., xr} называется базисом, а остальные неизвестные {xr+1, xr+2, ..., xn} - свободные. Подставляя (7.86) в (7.81), выразим функцию
f через свободные неизвестные:
f
= c0
+ c'r+1xr+1
+ c'хr+2 +…+ с'nxn.
Положим все свободные неизвестные равными нулю:
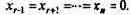
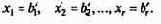
Полученное таким образом допустимое решение
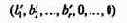
отвечает базису x1, х2, ..., xr,
т.е. является базисным решением. Допустим для определенности, что мы ищем минимум f. Теперь нужно отданного базиса перейти к другому с таким расчетом, чтобы значение линейной функции f при этом уменьшилось. Проследим идею симплекс-метода на примере.
Пример
1. Дана система ограничений
 |
x1 – 3x2 + 5x3 – x4 = 2
x1 + x2 + x3 + x4
= 4
Требуется минимизировать линейную функцию
f = х2 – x3. В качестве свободных переменных выберем х2
и х3. Тогда данная система ограничений преобразуется к виду
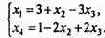
Таким образом, базисное решение (3, 0, 0, 1). Так как линейная функция уже записана в свободных неизвестных, то ее значение для данного базисного решения f = 0. Для уменьшения этого значения можно уменьшить x2 или увеличить x3. Но x2 в данном базисе равно нулю и потому его уменьшать нельзя.
Попробуем увеличить x3. Первое из уравнений имеет ограничение x3
= 1 (из условия x1 ? 0), второе - не дает ограничений. Далее, берем x3 = 1, х2
не меняем и получаем новое допустимое решение (0, 0, 1, 3), для которого f = -1 - уменьшилось. Найдем базис, которому соответствует это решение (он состоит, очевидно, из переменных x3, x4). От предыдущей системы ограничений переходим к новой:
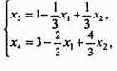
а форма в новых свободных переменных имеет вид
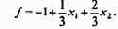
Теперь попробуем повторить предыдущую процедуру. Для уменьшения f надо уменьшить либо x1,
либо x2, но это невозможно, так как в этом базисе x1 = 0, x2 = 0.
Таким образом, данное базисное решение является оптимальным, и minf= -1 при x1
= 0, x2 = 0, x3 = 1, x4 = 3.
Приведем алгоритм симплекс-метода в общем виде. Обычно все вычисления по симплекс-методу сводят в стандартные таблицы.
Запишем систему ограничений в виде

а функцию f
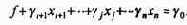
Тогда очередной шаг симплекс-процесса будет состоять в переходе от старого базиса к новому таким образом, чтобы значение линейной функции, по крайней мере, не увеличивалось.
Данные о коэффициентах уравнений и линейной функции занесем в табл. 7.12.
Таблица 7.12
Симплекс-таблица
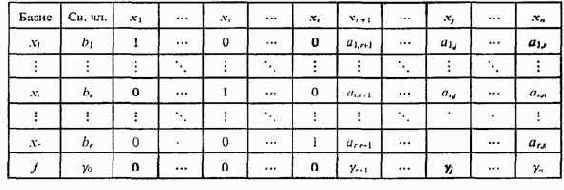
Сформулируем алгоритм симплекс-метода применительно к данным, внесенным в табл. 7.12.
1. Выяснить, имеются ли в последней строке таблицы положительные числа (?0 не принимается во внимание). Если все числа отрицательны, то процесс закончен; базисное решение (b1, b2, .... br, 0, ..., 0) является оптимальным; соответствующее значение целевой функции f = ?0. Если в последней строке имеются положительные числа, перейти к п.2.
2. Просмотреть столбец, соответствующий положительному числу из последней строки, и выяснить, имеются ли в нем положительные числа. Если ни в одном из таких столбцов положительных чисел нет, то оптимального решения не существует. Если найден столбец, содержащий хотя бы один положительный элемент (если таких столбцов несколько, взять любой из них), пометить этот столбец и перейти к п. 3.
3. Разделить свободные члены на соответствующие положительные числа из выделенного столбца и выбрать наименьшее частное. Отметить строку таблицы, соответствующую наименьшему частному. Выделить разрешающий элемент, стоящий на пересечении отмеченных строки и столбца. Перейти к п. 4.
4. Разделить элементы выделенной строки исходной таблицы на разрешающий элемент (на месте разрешающего элемента появится единица). Полученная таким образом новая строка пишется на месте прежней в новой таблице. Перейти к п. 5.
5. Каждая следующая строка новой таблицы образуется сложением соответствующей строки исходной таблицы и строки, записанной в п. 4. которая предварительно умножается на такое число, чтобы в клетках выделенного столбца при сложении появились нули. На этом процесс заполнения новой таблицы заканчивается, и происходит переход к п. 1.
Таким образом, используя алгоритм симплекс-метода применительно к симплекс-таблице, мы можем найти оптимальное решение или показать, что его не существует. Результативность симплекс-метода гарантируется следующей теоремой (приведем ее без доказательства): если существует оптимальное решение задачи линейного программирования, то существует и базисное оптимальное решение. Это решение может быть получено через конечное число шагов симплекс-методом, причем начинать можно с любого исходного базиса.
Ранее мы предполагали, что если система ограничений задана в виде (7.85), то перед первым шагом она уже приведена к виду (7.86), где bi ? 0 (i = 1, 2, ..., r). Последнее условие необходимо для использования симплекс-метода. Рассмотрим вопрос об отыскании начального базиса.
Один из методов его получения - метод симплексного преобразования.
Прежде всего проверяем, есть ли среди свободных членов отрицательные. Если свободные члены не являются числами неотрицательными, то добиться их неотрицательности можно несколькими способами:
1) умножить уравнения, содержащие отрицательные свободные члены, на-1;
2) найти среди уравнений, содержащих отрицательные свободные члены, уравнение с максимальным по абсолютной величине отрицательным свободным членом и затем сложить это уравнение со всеми остальными, содержащими отрицательные свободные члены, предварительно умножив его на-1.
Затем, используя действия, аналогичные указанным в пп. 3 - 5 алгоритма симплекс-метода, совершаем преобразования исходной таблицы до тех пор, пока не получим неотрицательное базисное решение.
Пример 2. Найти исходное неотрицательное базисное решение системы ограничений
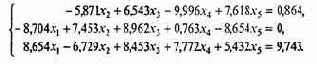
Так как условие неотрицательности свободных членов соблюдается, приступим к преобразованиям исходной системы, записывая результаты в таблицу. Согласно алгоритму просматриваем первый столбец. В этом столбце имеется единственный положительный элемент a31. Делим на 8,654 все коэффициенты и свободный член третьей строки, после чего умножаем каждый коэффициент на 8,704 и складываем с соответствующими коэффициентами второй строки. Первая строка преобразований не требует, так как коэффициент при неизвестном x1 равен нулю. В результате получаем
|
0,00000 0,00000 1,00000 |
-5,87100 0,68512 -0,77756 |
6,54300 17,46384 0,97677 |
-9,99600 8,57990 0,89808 |
7,61800 -3,19062 0,62769 |
0,86400 9,79929 1,11584 |
|
0,00000 0,00000 1,00000 |
0,00000 1,00000 0,00000 |
156,19554 25,49013 20,79687 |
63,52761 12,52318 10,63560 |
-19,72328 -4,65701 -2,99341 |
84,83688 14,30299 12,24727 |
x3. Неизвестные x4, х5
являются свободными:
|
0,00000 0,00000 1,00000 |
0,00000 1,00000 0,00000 |
1,00000 0,00000 0,00000 |
0,40672 2,15588 2,17713 |
-0,12627 -1,43829 -0,36733 |
0,54315 0,45815 0,95155 |
СИСТЕМА АНАЛИТИЧЕСКИХ ПРЕОБРАЗОВАНИЙ REDUCE
Развитие вычислительной техники начиналось с автоматизации выполнения арифметических действий. Вместе с тем известно, что компьютеры могут успешно оперировать математическими символами. Область вычислительной математики, связанная с аналитическими преобразованиями и получившая название компьютерной алгебры, в настоящее время развивается и получает широкое распространение в различных направлениях науки и образования. Основным объектом, над которым производит действие компьютер, является аналитическое (символьное) выражение, организованное и преобразуемое по заданным логическим правилам. Сегодня возможно компьютерное интегрирование и дифференцирование символьных выражений, перестановки и перегруппировки членов, приведение подобных членов, подстановки в выражения с последующим их преобразованием.
Очевидно, что известные системы программирования (Паскаль, СИ, Бейсик и т.п.) мало пригодны для анализа и преобразования символьной информации. Для этих целей созданы и развиваются специальные системы аналитических преобразований, которые можно разделить на универсальные, специализированные и общего назначения. Наибольшей популярностью пользуется универсальная система символьных вычислений REDUCE, автором которой является профессор А.Хиен. Система Reduce написана на языке высокого уровня ЛИСП.
Язык Reduce, составляющий ядро системы, трансляторы для которого разработаны для всех распространенных типов ЭВМ, предназначен прежде всего для проведения вычислении в аналитическом виде. Язык «знает» все операции алгебры с многочленами, приведением подобных членов, раскрытием скобок; все базовые элементарные функции, в том числе и в комплексной форме, ряд других функции; широкий набор операции над матрицами, включающий как входящие в обычные вузовские программы, так и выходящие за их пределы (например, функции от матриц); очень хорошо дифференцирует и несколько хуже вычисляет первообразные (но все же значительно лучше, чем большинство студентов, изучивших стандартный курс интегрального исчисления); умеет делать и ряд других действий.
Запуск программы на выполнение в системе осуществляется клавишей <Enter>.
Ниже приведем несколько примеров программ в системе Reduce, которые позволят получить первоначальные представления о системах аналитических преобразований символьной информации.
Пример 1.
А; XI; SS# ABCDIF; <Enter>
Листинг результата программы следующий:
А
XI
ABCDIF
Комментарий: все переменные являются свободными, т.е. их значения совпадают с именами.
Пример 2.
А:=123456789# В:= 123456789123456789#А*В; <Enter>
Листинг результата программы следующий:
15241578765432099750190521
Комментарий: переменным А и В присваиваются целочисленные значения и вычисляется их произведение, причем результат вычисления точный без округления.
Пример 3.
A:=S# A; A:=X*Y# A; Q:=X:=Y# Q; X; <Enter>
Листинг результата программы следующий:
S
Х*У
Y
Y
Комментарий: переменной А присваивается сначала значение S, затем - X*Y.
Пример 4.
13; 3+6; 2**64; 11-20; 25/(-125); 2*(3*A-6)/6; <Enter>
Листинг результата программы следующий:
139 18446744073709551616 (-9) (-1)/5А-2
Комментарий: при проведении алгебраических преобразований для записи сложных выражений используют имена переменных и знаки арифметических операций.
Пример5.
I**2; A:=X+I*Y# B:=X-I*Y# A*B; A**2; <Enter>
Листинг результата программы следующий:
-1
X-52-0+Y-52
' 2*I*X*Y + X-52-0-Y-52
Комментарий: для использования комплексных чисел за латинской буквой I закреплено значение мнимой единицы.
Пример 6.
OPERATOR F,W; W(X); F(5*X); (F(X)+A)**2; <Enter>
Листинг результата программы следующий:
W(X) F(5*X) F(X)-52-0 + 2*A*-F(x) + A-52
Комментарий: имена в скобках используют для обозначения операторов или функций, которые описываются предварительно командой OPERATOR.
Пример 7.
DF(X**2,X); DF(Y,Y,2); DF(X**3*Y*82*Z**3,X,3,Y,Z,2); DF(Y,X); <Enter>
Листинг результата программы следующий: 2*Х 0 72*Y*Z О
Комментарий: встроенный оператор DF используется для вычисления частных производных по отношению к одной или нескольким переменным, первым аргументом в скобках является дифференцируемое выражение, далее - аргументы, по которым проводится дифференцирование, и числа, указывающие порядок производной.
Пример 8.
INT(X**2,X); INT(SIN(X),X); <Enter>
Листинг результата программы следующий:
Х-53-0/3 - COS(X)
Комментарий: оператор INT используется для вычисления интегралов, на первом месте стоит интегрируемое алгебраическое выражение, на втором месте указывается переменная интегрирования.
Мы привели наиболее простые возможности системы Reduce. Подробнее ознакомиться с работой подобных систем читателю рекомендуется по специальным учебным пособиям и монографиям.
Контрольные вопросы
1. В чем основные отличия переменных в традиционных системах программирования от систем аналитических преобразований типа REDUCE?
2. В каких задачах предпочтительнее использовать методы компьютерной алгебры?
СИСТЕМА КОМАНД
Перейдем к самому важному - системе команд, которые умеет выполнять учебный процессор. Как мы уже знаем, машинная команда состоит из операционной и адресной частей: первая указывает, что надо сделать с данными, а вторая - где их взять и куда поместить результат. В этом разделе мы будем говорить, в основном, об операционной части, лишь коротко упоминая об адресной; в последней нас пока, главным образом, будет интересовать число операндов (адресов). Вопросам, связанным с подробностями адресации данных, будет посвящен следующий пункт.
Итак, рассмотрим структуру команды «Е97» (рис. 4.20). В зависимости от конкретной операции, ее формат может иметь некоторые особенности, но в наиболее полной форме он состоит из четырех частей по 4 бита каждая (см. рис. 4.20, б): модификатор МОД,
код операции КОП и два операнда ОП1 и ОП2. Назначение КОП и операндов было описано в предыдущем параграфе. Что же касается МОД, то он указывает варианты реализации команды, например, адресовать байт или слово, по каким управляющим битам переходить и др.
Наиболее простой формат команд из всех возможных, имеют две -нет операции (ее код 0) и останов (код F). Как видно из рис. 4.20, а, в этих командах задействован только КОП. остальные 12 бит значения не имеют. Основная масса команд, коды которых заключены в интервале от 1 до В. являются двухадресными и соответствуют уже упоминавшемуся ранее рис. 4.16, б. К ним относятся:
1 - перепись, 5 - умножение, 9 - исключающее «ИЛИ»,
2 - сложение, 6 - деление, А - ввод из порта,
3 - вычитание, 7 - логическое «И», В - вывод из порта.
4 - сравнение, 8 - «ИЛИ»,
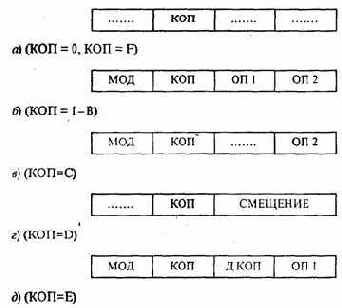
Рис. 4.20. Форматы команд учебного процессора «Е97»
Операция переписи выполняется достаточно тривиально: информация считывается из ОП1 и копируется в ОП2. Совершенно аналогично работают ввод и вывод из порта, с той лишь разницей, что в качестве одного из операндов указывается номер порта.
Все остальные двухадресные команды с кодами 2- 9 представляют собой определенные действия над двумя данными, выполняемые по универсальной схеме
ОП2 операция ОП 1 => ОП2
Например, по команде деления процессор извлекает ОП2, делит его на ОП1 и результат помещает вместо первоначального значения ОП2.
Некоторую особенность имеет команда сравнения. При ее исполнении производится вычитание ОП2 - ОП1, но результат никуда не записывается. («Тогда для чего же вычитать?» - спросите вы? - «Исключительно ради установки управляющих битов, которые в дальнейшем могут быть проанализированы командами условных переходов».)
Арифметические действия осуществляются над целыми числами и результаты их -целочисленные в формате «16-битные целые числа со знаком». При делении получается целая часть частного. Что же касается операций над вещественными числами, то они могут быть реализованы программным путем (соответствующие программы могут быть, например, помещены в одно из ПЗУ).
Перейдем теперь к рассмотрению команд переходов. Как мы уже знаем, они бывают абсолютные,
когда значение адреса для перехода задается явно, и относительные. когда адрес следующей команды вычисляется путем значения текущего программного счетчика и указанного в теле команды смещения. В соответствии с этим в «Е97» есть два типа переходов с кодами операций С и D; их форматы представлены на рис. 4.20, в, г.
Начнем с абсолютного перехода, код которого равен С. Если процессор встретит в программе команду из двух слов
1C0D
0056
то следующей будет выполняться команда с адресом 56. Иными словами, адрес перехода берется из самой команды. В команде 1C0D старшая шестнадцатеричная цифра - модификатор, соответствующий безусловному переходу; С - код операции; 0 - неиспользуемая цифра; D - операнд, указывающий что адрес перехода хранится в следующем слове, составляющем с 1C0D единое целое. Подробности такого способа адресации - в следующем пункте.
По-другому обстоит дело с относительным переходом, код которого D. В качестве примера возьмем команду
1D06
Для определенности будем считать, что эта команда находится в памяти по адресу 42. В строгом соответствии с основным алгоритмом работы процессора, после выборки рассматриваемой команды счетчик адреса команд PC автоматически увеличивается до 44. Затем, выполняя расшифрованную команду перехода, процессор прибавит к текущему содержимому PC смещение 06 и тем самым осуществит переход на адрес 44 + 6 = 4А. Обратите внимание, что итоговый адрес в случае относительного перехода зависит от расположения команды перехода в ОЗУ.
При отрицательном смещении возможно получение адреса меньшего, чем исходный. При обсуждении команд перехода мы незаметно включили в работу модификатор команд. Для переходов его роль проста и наглядна: МОД показывает, по какому условию осуществляется переход. Таблица всех используемых в «Е97» значений модификаторов выглядит так:
0 - возврат из подпрограммы;
1 - безусловный переход;
2 - N = 0 (?0);
3 - N = 1 (<0);
4 - Z =
0 (?0);
5 - Z =
1 (=0);
6 - N=1 orZ=l (?0);
'7 - N=0andZ=0(>0);
9 - вызов подпрограммы.
Становится очевидным, что рассмотренные в обоих предыдущих примерах команды с МОД = 1 являются наиболее простым вариантом перехода - безусловным.
Для работы с условными переходами следует твердо запомнить следующее правило:
«Если анализируемое условие справедливо, т. е. состояние управляющих признаков совпадает с требуемым, то переход происходит. В противном случае никаких действий не производится, а значит переход просто игнорируется и процессор, как обычно, выбирает следующую команду».
Кстати, так обстоит дело и в языках высокого уровня.
И еще об одном виде перехода следует поговорить особо - о переходе с возвратом или о переходе к подпрограмме, как его часто называют. На практике подпрограммы (процедуры) и функции играют очень важную роль. Подпрограммы полезны, когда в разных местах программы требуется выполнить одни и те лее действия. В этом случае имеет смысл оформить повторяющиеся действия в виде подпрограммы, а затем просто вызывать ее в нужных местах.
В каком- то смысле это похоже на публикацию текстов песен, когда припев пишется один раз, а в дальнейшем просто ставится ссылка на него в виде слова «ПРИПЕВ».
Наиболее важное отличие перехода к подпрограмме от безусловного перехода состоит в том, что требуется иметь возможность вернуться из подпрограммы в то же самое место, откуда она была вызвана. Применительно к процессору возможность возврата означает запоминание где-нибудь значения программного счетчика PC; для возврата достаточно будет просто восстановить в PC сохраненное значение.
Для обеспечения возможности вложения друг в друга подпрограмм необходимо уметь сохранять не одно значение PC, а несколько. Для реализации такого механизма памяти используется стек, который идеально подходит для любой вложенности конструкций и при этом требует наличия всего одного выделенного регистра-указателя стека SP.
Рассмотрим конкретный пример. Пусть в некотором месте программы находится команда из двух слов
9C0D
0030
Исполнять эту команду процессор будет так. Прежде всего, он уменьшит SP на 2 и запомнит по полученному адресу текущее содержимое PC (вспомните, что счетчик к этому времени уже будет показывать на следующую команду). Затем последует переход по адресу 30, считанному ранее из второго слова команды. Таким способом мы попадем в подпрограмму, надежно спрятав в стеке адрес основной программы, куда нужно вернуться. Обсудим теперь, как произойдет возврат.
В конце любой подпрограммы должна стоять команда 0С00 или 0D00. Встретив ее. процессор извлечет из стека занесенное туда ранее значение и поместит его в PC. При этом он увеличит SP на два, освободив ненужную более ячейку памяти в стеке. Таким образом, прерванное на время выполнение основной программы продолжится с нужного места.
Примечание.
Команды с кодами 0С и 0D тождественны и их младшие 8 бит не используются.
Для того, чтобы лучше разобраться в описанном механизме, попробуйте самостоятельно проанализировать ситуацию, когда одна подпрограмма вызывает другую.
Займемся последней группой команд процессора, для которой КОП = Е.
Прежде всего, почему такому КОП соответствует группа, а не одна команда? Все дело в том, что эти команды одноадресные, и освобождающиеся от одного из операндов 4 бита можно использовать для задания номера операции в этой группе. Назовем полученные биты дополнением к КОП - ДКОП. В итоге получим формат, приведенный на рис.4.20, д). Из рисунка видно, что код операций для всех одноадресных операций состоит из двух шестнадцатеричных цифр, причем первая из них всегда Е. Познакомимся с этими командами более подробно.
Команда с кодом Е1 выполняет над единственным операндом ОП1 логическую операцию НЕ, т.е. заменяет нулевые биты единицами и наоборот (инверсия).
Команды с кодами Е2 - Е9 обеспечивают работу со стеком. Так, при коде операции Е2 ОП1 заносится в стек, а при ЕЗ - считывается оттуда. Например, вот как можно поменять местами содержимое регистров R1 и R2 с использованием стека:
0000 0Е21 записать R1 в стек
0002 0Е22 записать R2 в стек
0004 0Е31 считать значение из стекав R1
0006 0Е32 считать значение из стека в R2
0008 0F00 останов
Команды Е4 и Е5 позволяют изменять значение SP на величину ОП1, что часто бывает полезно при работе со стеком, например, при освобождении в нем сразу нескольких «этажей». По кодам Е6 и Е7 можно задать новое значение SP и прочитать его текущее значение в ОП1. Наконец, наиболее экзотические из этой группы команды Е8 и Е9 сохраняют в стеке и восстанавливают для последующего анализа регистр состояния процессора PS. Эти команды замечательны тем, что обрабатывают вполне определенный операнд, поэтому содержимое ОП1 в команде значения не имеет; договоримся заполнять его нулем.
Осталось рассмотреть последнюю группу команд - сдвиги. Их коды ЕА - ЕС. Все они осуществляют сдвиг кода в ОП1 на один разряд влево или вправо в зависимости от значения ДКОП. Полезно помнить, что сдвиг влево эквивалентен умножению, а вправо - делению на два.
Команда ЕС, называемая арифметическим сдвигом, отличается от обычного сдвига ЕВ тем, что старший знаковый разряд при арифметическом сдвиге сохраняет свое значение, например:
Исходное значение ОП 1: 1111 0000 1111 0000
Результат команды ЕВ: 0111 1000 0111 1000
Результат команды ЕС: 1111 1000 0111 1000.
Арифметический сдвиг бывает полезен для деления отрицательных чисел, так как в этом случае автоматически сохраняется признак знака минус - единица в старшем разряде.
В данной модели при сдвиге, приводящем в выходу старшей или младшей цифры за пределы разрядной сетки, соответствующая информация теряется. В реальных процессорах для ее сохранения существует специальный управляющий бит, называемый «битом переноса».
СИСТЕМА КОМАНД ЭВМ И СПОСОБЫ ОБРАЩЕНИЯ К ДАННЫМ
Важной составной частью архитектуры ЭВМ является система команд. Несмотря на большое число разновидностей ЭВМ, на самом низком («машинном») уровне они имеют много общего. Система команд любой ЭВМ обязательно содержит следующие группы команд обработки информации.
1. Команды передачи данных (перепись), копирующие информацию из одного места в другое.
2. Арифметические операции, которым фактически обязана своим названием вычислительная техника. Конечно, доля вычислительных действий в современном компьютере заметно уменьшилась, но они по-прежнему играют в программах важную роль. Отметим, что к основным арифметическим действиям обычно относятся сложение и вычитание (последнее в конечном счете чаще всего тем или иным способом также сводится к сложению). Что касается умножения и деления, то они во многих ЭВМ выполняются по специальным программам.
3. Логические операции, позволяющие компьютеру анализировать обрабатываемую информацию. Простейшими примерами могут служить сравнение, а также известные логические операции И, ИЛИ, НЕ (инверсия). Кроме того к ним часто добавляются анализ отдельных битов кода, их сброс и установка.
4. Сдвиги двоичного кода влево и вправо. Для доказательства важности этой группы команд достаточно вспомнить правило умножения столбиком: каждое последующее произведение записывается в такой схеме со сдвигом на одну цифру влево. В некоторых частных случаях умножение и деление вообще может быть заменено сдвигом (вспомните, что дописав или убрав ноль справа, т.е. фактически осуществляя сдвиг десятичного числа, можно увеличить или уменьшить его в 10 раз).
5. Команды ввода и вывода информации для обмена с внешними устройствами. В некоторых ЭВМ внешние устройства являются специальными служебными адресами памяти, поэтому ввод и вывод осуществляется с помощью команд переписи.
6. Команды управления, реализующие нелинейные алгоритмы. Сюда прежде всего следует отнести условный и безусловный переход, а также команды обращения к подпрограмме (переход с возвратом).
Некоторые ЭВМ имеют специальные команды для организации циклов, но это не обязательно: цикл может быть сведен к той или иной комбинации условного и безусловного переходов. Часто к этой же группе команд относят немногочисленные операции по управлению процессором -типа «останов» или НОП («нет операции»). Иногда их выделяют в особую группу.
С ростом сложности устройства процессора увеличивается и число команд, анализирующих состояние управляющих битов и воздействующих на них. Здесь для примера можно назвать биты режима работы процессора и биты управления механизмами прерываний от внешних устройств.
В последнее время все большую роль в наборе команд играют команды для преобразования из одного формата данных в другой (например, из 8-битного в 16-битный и т.п.), которые заметно упрощают обработку данных разного типа, но в принципе могут быть заменены последовательностью из нескольких более простых команд.
Рассматривая систему команд, нельзя не упомянуть о двух современных взаимно конкурирующих направлениях в ее построении: компьютер с полным набором команд CISC (Complex Instruction Set Computer) и с ограниченным набором - RISC (Reduced Instruction Set Computer). Разделение возникло из-за того, что основную часть времени компьютеру приходится выполнять небольшую часть из своего набора команд, остальные же используются эпизодически (в одной из популярных статей это в шутку сформулировано в виде следующей наглядной аналогии: «20% населения выпивают 80% пива»). Таким образом, если существенно ограничить набор операций до наиболее простых и коротких, зато тщательно оптимизировать их, получится достаточно эффективная и быстродействующая RISC-машина. Правда за скорость придется платить необходимостью программной реализации «отброшенных» команд, но часто эта плата бывает оправданной: например, для научных расчетов или машинной графики быстродействие существенно важнее проблем программирования. Подробнее вопросы, связанные с системой команд современных микропроцессоров, будут рассмотрены ниже в этой главе.
Подводя итог, еще раз подчеркнем, что основной набор команд довольно слабо изменился в ходе бурной эволюции ЭВМ. В то же время способы указания адреса расположения информации в памяти претерпели значительное изменение и заслуживают особого рассмотрения.
Команда ЭВМ обычно состоит из двух частей - операционной и адресной. Операционная часть (иначе она еще называется кодом операции - КОП) указывает, какое действие необходимо выполнить с информацией. Адресная часть описывает, где используемая информация хранится. У нескольких немногочисленных команд управления работой машины адресная часть может отсутствовать, например, в команде останова; операционная часть имеется, всегда.
Код операции можно представить себе как некоторый условный номер в общем списке системы команд. В основном этот список построен в соответствии с определенными внутренними закономерностями, хотя они не всегда очевидны.
Адресная часть обладает значительно большим разнообразием и ее следует рассмотреть подробнее.
Прежде всего отметим, что команды могут быть одно-, двух- и трехадресные в зависимости от числа участвующих в них операндов.
Первые ЭВМ имели наиболее простую и наглядную трехадресную систему команд. Например: взять числа из адресов памяти А1 и А2, сложить их и сумму поместить в адрес A3. Если для операции требовалось меньшее число адресов, то лишние просто не использовались. Скажем, в операции переписи указывались лишь ячейки источника и приемника информации А1 и A3, а содержимое А2 не имело никакого значения.
Трехадресная команда легко расшифровывалась и была удобна в использовании, но с ростом объемов ОЗУ ее длина становилась непомерно большой. Действительно, длина команды складывается из длины трех адресов и кода операции. Отсюда следует, например, что для скромного ОЗУ из 1024 ячеек только для записи адресной части одной команды требуется 3*10 = 30 двоичных разрядов, что для технической реализации не очень удобно. Поэтому появились двухадресные машины, длина команды в которых сокращалась за счет исключения адреса записи результата.
В таких ЭВМ результат операции оставался в специальном регистре (сумматоре) и был пригоден для использования в последующих вычислениях. В некоторых машинах результат записывался вместо одного из операндов.
Дальнейшее упрощение команды привело к созданию одноадресных машин. Рассмотрим систему команд такой ЭВМ на конкретном простом примере. Пусть надо сложить числа, хранящиеся в ячейках с адресами ОЗУ А1 и А2, а сумму поместить в ячейку с адресом A3. Для решения этой задачи одноадресной машине потребуется выполнить три команды:
• извлечь содержимое ячейки А1 в сумматор;
• сложить сумматор с числом из А2;
• записать результат из сумматора в A3.
Может показаться, что одноадресной машине для решения задачи потребуется втрое больше команд, чем трехадресной. На самом деле это не всегда так. Попробуйте самостоятельно спланировать программу вычисления выражения А5 = (А1 + А2)*АЗ/А4 и вы обнаружите, что потребуется три трехадресных команды и всего пять одноадресных. Таким образом, одноадресная машина в чем-то даже эффективнее, так как она не производит ненужной записи в память промежуточных результатов.
Ради полноты изложения следует сказать о возможности реализации безадресной (нуль-адресной) машины, использующей особый способ организации памяти -стек. Понимание принципов устройства такой машины потребовало бы некоторых достаточно подробных разъяснений. Сейчас безадресные ЭВМ практически не применяются. Поэтому ограничимся лишь упоминанием того факта, что устроенная подобным образом система команд лежала в основе некоторых программируемых микрокалькуляторов (например, типа «БЗ-21» и «БЗ-34» и им подобных).
До сих пор в описании структуры машинной команды мы пользовались интуитивным понятием об адресе информации. Рассмотрим теперь вопрос об адресации элементов ОЗУ более подробно и строго. Наиболее просто была организована память в ЭВМ первых двух поколений. Она состояла из отдельных ячеек, содержимое каждой из которых считывалось или записывалось как единое целое. Каждая ячейка памяти имела свой номер, который и получил название адреса.
Очевидно, что адреса соседних ячеек ОЗУ являются последовательными целыми числами, т.е. отличаются на единицу. В рассматриваемых ЭВМ использовались данные только одного типа (вещественные числа), причем их длина равнялась длине машинной команды и совпадала с разрядностью памяти и всех остальных устройств машины. Для примера укажем, что ячейка типичной ЭВМ второго поколения состояла из 36 двоичных разрядов.
Очень часто программа предназначалась для обработки по одним и тем же формулам определенного количества содержимого последовательно расположенных ячеек (в языках высокого уровня такого рода структуры получили впоследствии название массивов). В ЭВМ первых двух поколении были предусмотрены особые механизмы циклической обработки массивов информации. С этой целью в машинных командах помимо обычных адресов можно было использовать модифицируемые, у которых специальный управляющий бит был установлен в единицу. К помеченным таким образом модифицируемым адресам при выполнении команды прибавлялось значение из специальных индексных ячеек. Меняя содержимое индексных ячеек, можно было получать доступ к различным элементам массива. Особо подчеркнем, что формирование результирующего адреса осуществлялось в УУ в момент исполнения команды, поэтому исходная команда в ОЗУ сохранялась без изменений.
Описанный механизм модификации адресов существенно упрощал написание циклических программ, таких как нахождение суммы последовательных ячеек ОЗУ, копирование отдельных участков памяти и т.п.
В ЭВМ третьего поколения идеология построения памяти существенно изменилась: минимальная порция информации для обмена с ОЗУ была установлена равной 8 двоичных разрядов, т.е. один байт. Стало возможным обрабатывать несколько типов данных: символы текста (1 байт), целые числа (2 байта), вещественные числа обычной или двойной точности (4 или 8 байт соответственно). В связи с этим была введена новая условная единица измерения информации - машинное слово. Оно равнялось 4 байтам и соответствовало длине стандартного вещественного числа.
Все объемы информации начали измеряться в единицах, кратных слову: двойное слово, полуслово и т.п. Естественно, что адрес (номер ячейки ОЗУ) в машинах с байтовой организацией стал относится к отдельному байту; байты памяти имеют возрастающие на единицу номера. Слово состоит из нескольких последовательно расположенных байтов. В качестве адреса слова удобно принимать адрес одного из образующих его байтов (обычно используется младший байт, имеющий наименьший номер). Таким образом, адреса слов меняются уже не через единицу; их приращение зависит от длины машинного слова в байтах и равняется четырем.
Размер машинного слова был, по-видимому, выбран исходя из форматов обрабатываемой информации, а не в связи с разрядностью каких-либо устройств. Для подтверждения этого приведем несколько фактов о типичных ЭВМ третьего поколения из семейства ЕС. Арифметико-логическое устройство модели «ЕС-1022» имело 16 двоичных разрядов, «ЕС-1033» - 32 разряда, а «ЕС-1050» - 64 разряда. В то же время за одно обращение к оперативной памяти в «ЕС-1022» и «ЕС-1033» выбиралось 4 байта, в «ЕС-1050» - 8 байт (а в «ЕС-1045» - 16 байт). Таким образом, разнообразие цифр свидетельствует, что 32 разряда (4 байта) не являлись каким-то технически выделенным объемом информации.
В машинах третьего поколения появились и еще несколько особенностей: разная длина команд в зависимости от способа адресации данных, наличие специальной сверхоперативной регистровой памяти, вычисление эффективного адреса ОЗУ как суммы нескольких регистров и т.п. Все это получило дальнейшее развитие в компьютерах четвертого поколения, для которых разрядность микропроцессора стала одной из важнейших характеристик. Рассмотрение особенностей строения памяти ЭВМ четвертого поколения отложим до следующего раздела.
СИСТЕМЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ
Близкими по своей структуре и функциям к системам автоматизации научных исследований оказываются системы автоматизированного проектирования (САПР), знакомство с которыми было начато в главе 2. Здесь мы ограничимся взглядом на САПР как на сложную информационную систему.
Проектирование новых изделий - основная задача изобретателей и конструкторов - протекает в несколько этапов, таких как формирование замысла, поиск физических принципов, обеспечивающих реализацию замыслов и требуемые значения параметров конструкции, поиск конструктивных решении, их расчет и обоснование, создание опытного образца, разработка технологии промышленного изготовления. Если формирование замысла и поиск физических принципов пока остаются чисто творческими, не поддающимися автоматизации этапами, то при конструировании и
расчетах с успехом могут быть применены САПР, рис. 6.10.
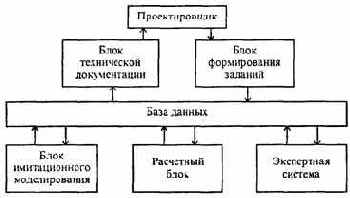
Рис. 6.10. Типовая схема САПР
База данных, блок имитационного моделирования, расчетный блок и экспертная система выполняют функции, аналогичные функциям соответствующих блоков АСНИ. Вместо блока связи с измерительной аппаратурой в САПР имеется блок формирования заданий. Проектировщик вводит в блок техническое задание на проектирование, в котором указаны цели, которые необходимо достичь при проектировании, и все ограничения, которые нельзя нарушить. Блок подготовки технической документации облегчает создание технической документации для последующего изготовления изделия.
В настоящее время САПР является неотъемлемым атрибутом крупных конструкторских бюро и проектных организаций, работающих в различных предметных областях. Это важная сфера приложения идей и методов информатики.
СОЦИАЛЬНЫЕ АСПЕКТЫ ИНФОРМАТИКИ
Термин «социальные аспекты» применительно к большей части наук, тем более фундаментальных, звучит странно. Вряд ли фраза «Социальные аспекты математики» имеет смысл. Однако, информатика - не только наука. Вспомним цитированное выше определение: «... комплекс промышленного, коммерческого, административного и социального воздействия».
И впрямь, мало какие факторы так влияют на социальную сферу обществ (разумеется, находящихся в состоянии относительно спокойного развития, без войн и катаклизмов) как информатизация. Информатизация общества - процесс проникновения информационных технологий во все сферы жизни и деятельности общества. Многие социологи и политологи полагают, что мир стоит на пороге информационного общества. В. А. Извозчиков предлагает следующее определение: «Будем понимать под термином «информационное» («компьютеризиро-ванное») общество то, во все сферы жизни и деятельности членов которого включены компьютер, телематика, другие средства информатики в качестве орудий интеллектуального труда, открывающих широкий доступ к сокровищам библиотек, позволяющих с огромной скоростью проводить вычисления и перерабатывать любую информацию, моделировать реальные и прогнозируемые события, процессы, явления, управлять производством, автоматизировать обучение и т.д.». Под «телематикой» понимаются службы обработки информации на расстоянии (кроме традиционных телефона и телеграфа).
Последние полвека информатизация является одной из причин перетока людей из сферы прямого материального производства в, так называемую, информационную сферу. Промышленные рабочие и крестьяне, составлявшие в середине XX века более 2/3 населения,,сегодня в развитых странах составляют менее 1/3. Все больше тех, кого называют «белые воротнички» - людей, не создающих материальные ценности непосредственно, а занятых обработкой информации (в самом широком смысле): это и учителя, и банковские служащие, и программисты, и многие другие категории работников. Появились и новые пограничные специальности.
Можно ли назвать рабочим программиста, разрабатывающего программы для станков с числовым программным управлением? - По ряду параметров можно, однако его труд не физический, а интеллектуальный.
В табл.1 приведены статистические данные, описывающие изменения в профессиональной структуре труда в США (стране, где информатизация идет особенно быстро) за период с 1970 по 1980 г.
Таблица 1.1 Изменения в структуре труда США за 10 лет
|
Категория работающих |
1970г., % |
1980г.,% |
Относительный прирост численности, % |
|
Работники сервиса |
19,9 |
21,5 |
+0,1 |
|
Рабочие (промышленные, сельскохозяйственные, фермеры) |
38,7 |
34,2 |
-11,6 |
|
Занятые обработкой информации (всего) |
41,5 |
44,4 |
+6,7 |
|
в том числе: менеджеры |
8,5 |
8,7 |
+2,4 |
|
конторские служащие |
18,0 |
18,9 |
+5,0 |
|
специалисты с высшим образованием |
15,0 |
16,8 |
+12,0 |
Таблица 1.2. Профессиональная структура занятости в экономике США
(по данным на 1980 г.)
|
Отрасль |
Работают с информацией, % |
Работают с материальными объектами, % |
|
Обрабатывающая промышленность Транспорт и связь Оптовая торговля Розничная торговля Сфера услуг Финансовая деятельность Государственные учреждения |
40 44 68 58 63 92 70 |
60 56 32 42 37 8 30 |
За годы, прошедшие с момента публикации этих данных, ситуация изменилась в сторону дальнейшего увеличения доли населения, занятого в профессиональном труде обработкой информации. К середине 90-х годов численность «информационных работников» (к которым причисляют всех, в чьей профессиональной деятельности доминирует умственный труд) достигла в США 60%.
Добавим, что за те же годы производительность труда в США за счет научно-технического прогресса (ведь информатизация - его главная движущая сила) в целом выросла на 37%.
Информатизация сильнейшим образом влияет на структуру экономики ведущих в экономическом отношении стран. В числе их лидирующих отраслей промышленности традиционные добывающие и обрабатывающие отрасли оттеснены максимально наукоемкими производствами электроники, средств связи и вычислительной техники (так называемой, сферой высоких технологий). В этих странах постоянно растут капиталовложения в научные исследования, включая фундаментальные науки. Темпы развития сферы высоких технологий и уровень прибылей в ней превышают в 5-10 раз темпы развития традиционных отраслей производства. Такая политика имеет и социальные последствия - увеличение потребности в высокообразованных специалистах и связанный с этим прогресс системы высшего образования. Информатизация меняет и облик традиционных отраслей промышленности и сельского хозяйства. Промышленные роботы, управляемые ЭВМ, станки с ЧПУ стали обычным оборудованием. Новейшие технологии в сельскохозяйственном производстве не только увеличивают производительность труда, но и облегчают его, вовлекают более образованных людей.
Казалось бы, компьютеризация и информационные технологии несут в мир одну лишь благодать, но социальная сфера столь сложна, что последствия любого, даже гораздо менее глобального процесса, редко бывают однозначными. Рассмотрим, например, такие социальные последствия информатизации как рост производительности труда, интенсификацию труда, изменение условий труда. Все это, с одной стороны, улучшает условия жизни многих людей, повышает степень материального и интеллектуального комфорта, стимулирует рост числа высокообразованных людей, а с другой - является источником повышенной социальной напряженности. Например, появление на производстве промышленных роботов ведет к полному изменению технологии, которая перестает быть ориентированной на человека.
Тем самым меняется номенклатура профессий. Значительная часть людей вынуждена менять либо специальность, либо место работы - рост миграции населения характерен для большинства развитых стран. Государство и частные фирмы поддерживают систему повышения квалификации и переподготовки, но не все люди справляются с сопутствующим стрессом. Прогрессом информатики порожден и другой достаточно опасный для демократического общества процесс - все большее количество данных о каждом гражданине сосредоточивается в разных (государственных и негосударственных) банках данных. Это и данные о профессиональной карьере (базы данных отделов кадров), здоровье (базы данных учреждений здравоохранения), имущественных возможностях (базы данных страховых компаний), перемещении по миру и т.д. (не говоря уже о тех, которые копят специальные службы). В каждом конкретном случае создание банка может быть оправдано, но в результате возникает система невиданной раньше ни в одном тоталитарном обществе прозрачности личности, чреватой возможным вмешательством государства или злоумышленников в частную жизнь. Одним словом, жизнь в «информационном обществе» легче, по-видимому, не становится, а вот то, что она значительно меняется - несомненно.
Трудно, живя в самом разгаре описанных выше процессов, взвесить, чего в них больше - положительного или отрицательного, да и четких критериев для этого не существует. Тяжелая физическая работа в не слишком комфортабельных условиях, но с уверенностью, что она будет постоянным источником существования для тебя и твоей семьи, с одной стороны, или интеллектуальный труд в комфортабельном офисе, но без уверенности в завтрашнем дне. Что лучше? Конечно, вряд ли стоит уподобляться английским рабочим, ломавшим в конце XVIII века станки, лишавшие их работы, но правительство и общество обязаны помнить об отрицательных социальных последствиях информатизации и научно-технического прогресса в целом и искать компенсационные механизмы.
СОСТАВ И ФУНКЦИИ СИСТЕМ УПРАВЛЕНИЯ БАЗАМИ ДАННЫХ
База данных предполагает наличие комплекса программных средств, обслуживающих эту базу данных и позволяющих использовать содержащуюся в ней информацию. Такие комплексы программ называют СУБД. СУБД - это программная система, поддерживающая наполнение и манипулирование данными, представляющими интерес для пользователей при решении прикладных задач. Иными словами, СУБД является интерфейсом между базой данных и прикладными задачами.
Ниже перечислены основные функции СУБД.
1. Определение данных - определить, какая именно информация будет храниться в базе данных, задать свойства данных, их тип (например, число цифр или символов), а также указать, как эти данные связаны между собой. В некоторых случаях есть возможность задавать форматы и критерии проверки данных.
2. Обработка данных
- данные могут обрабатываться самыми различными способами. Можно выбирать любые поля, фильтровать и сортировать данные. Можно объединять данные с другой, связанной с ними, информацией и вычислять итоговые значения.
3. Управление данными
- можно указать, кому разрешено знакомиться с данными, корректировать их или добавлять новую информацию. Можно также определять правила коллективного доступа.
Входящие в состав современных СУБД средства совместно выполняют следующие функции:
• описание
данных, их структуры (обычно описание данных и их структуры происходит при инициировании новой базы данных или добавлении к существующей базе новых разделов (отношений); описание данных необходимо для контроля корректности использования данных, для поддержания целостности базы данных);
• первичный ввод, пополнение информации в базе данных;
• удаление
устаревшей информации из базы данных;
• корректировку
данных для поддержания их актуальности;
• упорядочение (сортировку) данных по некоторым признакам;
• поиск информации
по некоторым признакам (для описания запросов имеется специальный язык запросов, он обеспечивает также интерфейс между базой данных и прикладными программами пользователей, позволяет этим программам использовать базы данных);
• подготовку и генерацию отчетов ( средства подготовки отчетов позволяют создавать и распечатывать сводки по заданным формам на основе информации базы данных);
• защиту информации и разграничение доступа пользователей к ней (некоторые разделы базы данных могут быть закрыты для пользователя совсем, открыты только для чтения или открыты для изменения; кроме того, при многопользовательском режиме работы с базой данных необходимо, чтобы изменения вносились корректно; для сохранения целостности данных служит механизм трансакций при манипулировании данными - выполнение манипуляций небольшими пакетами, результаты каждого из которых в случае возникновения некорректности операций «откатываются» и данные возвращаются к исходному состоянию);
• резервное сохранение и восстановление базы данных, которое позволяет восстановить утраченную при сбоях и авариях аппаратуры информацию базы данных, а также накопить статистику работы пользователей с базой данных;
• поддержку интерфейса с пользователями, который обеспечивается средствами ведения диалога (по мере развития и совершенствования СУБД этот интерфейс становится все более дружественным; дружественность существующих средств интерфейса предполагает
• наличие развитой системы помощи (подсказки), к которой в любой момент может обратиться пользователь, не прерывая сеанса работы с компьютером и базой данных;
• защиту от необдуманных действий, предупреждающую пользователя и предотвращающую потерю информации в случае поспешных или ошибочных команд;
• наличие нескольких вариантов выполнения одних и тех же действий, из которых пользователь может выбрать наиболее удобные для себя, соответствующие его подготовке, квалификации, привычкам;
• тщательно продуманную систему ведения человеко-машинного диалога, отображение информации на дисплее, использование клавиш клавиатуры). В настоящее время выделяют пять уровней проблематики систем управления базами данных:
• реляционные базы данных, 1970 - 90 гг.;
• объектно-ориентированные базы данных, 1980 - 90 гг.;
• интеллектуальные базы данных, 1985 - 90 гг.;
• распределенные базы данных, начало 1990 гг.;
• базы данных мультимедиа и виртуальной реальности настоящего времени.
Архитектурно СУБД состоит из двух основных компонентов; языка описания данных
(ЯОД), позволяющего создать схему описания данных в базе, и языка манипулирования данными (ЯМД), выполняющего операции с базой данных (наполнение, обновление, удаление, выборку информации). Данные языки могут быть реализованы в виде тренажеров или интерпретаторов. Помимо ЯОД и ЯМД к СУБД следует отнести средства
(или языки) подготовки отчетов
(СПО), позволяющие подготовить сводки (отчеты) на основе информации, найденной в базе данных, по заданным формам.
Язык описания данных (ЯОД) - это язык высокого уровня декларативного (непроцедурного) типа, предназначенный для формализованного описания типов данных, их структур и взаимосвязей. Исходные тексты описания данных на этом языке после трансляции отображаются в управляющие таблицы, задающие размещение в памяти ЭВМ и связи между собой рассматриваемых данных. В соответствии с этими описаниями СУБД находит в базе требуемые данные, правильно преобразует их и передает, например, в прикладную программу пользователя, которой они потребовались. При записи данных в базу СУБД по этим описаниям определяет место в памяти ЭВМ, куда их требуется поместить, преобразует к заданному виду и устанавливает необходимые связи.
Язык манипулирования данными (или язык запросов) представляет собой систему команд, например, следующего типа:
• произвести выборку данного, значение которого удовлетворяет заданным условиям;
• произвести выборку всех данных определенного типа, значения которых удовлетворяют заданным условиям;
• найти в базе позицию данного и поместить туда новое значение (или удалить данное) и т.д.
Широкое распространение имеют СУБД для персональных компьютеров типа DBASE (DBASE III, IV, FoxPro, Paradox), Clipper, Clarion. Эти СУБД ориентированы на однопользовательский режим работы с базой данных и имеют очень ограниченные возможности.
Языки подобных СУБД представляют собой сочетание команд выборки, организации диалога, генерации отчетов. В связи с развитием компьютерных сетей, в которых персональные компьютеры выступают в качестве развитых (интеллектуальных) терминалов, новые версии СУБД все в большей степени включают в себя возможности описанного ниже языка манипулирования данными SQL.
В последнее время стали среди СУБД популярными ACCESS (входит в состав MS Office), Lotus, Oracle.
Язык манипулирования данными SQL
Рассмотрим в качестве примера языка манипулирования данными некоторые команды языка SQL (от английских слов Structured Query Language), ставшего классическим языком реляционных баз данных.
Простейшая операция выборки представляется командой SELECT - FROM -WHERE (выбрать - из - где):
select <список атрибутов>
from <отношение>
where <условие>.
Например, если необходимо из отношения «Успеваемость», имеющего схему:
Успеваемость (ФПО_студента, Дисциплина, Оценка, Дата, Преподаватель)
произвести выборку данных о том, какие оценки студент Иванов И.И. получил и по каким предметам, надо задать команду:
select Дисциплина, Оценка
from Успеваемость
where ФИО_студента = «Иванов И. И.».
Часть команды «where» не является обязательной. Например, можно получить список всех студентов из отношения «Успеваемость» с помощью следующей команды:
select unique ФИО_студента
from Успеваемость.
Ключевое слово unique позволяет исключить из результата дубликаты значений атрибута. Выбрать полностью информацию из таблицы можно с помощью команды
select *
from Успеваемость.
Условие, следующее за «where», может включать операторы сравнения =,
<>, >=, <, <=,
булевы операторы AND, OR, NOT, а также скобки для указания желаемого порядка операции. Например, выбрать из таблицы «Успеваемость» фамилии студентов, сдавших на "5" экзамен по информатике, можно с помощью команды
select ФИО_студента
from Успеваемость
where Дисциплина = «Информатика» AND Оценка=5.
Выборка может быть и вложенной, когда необходимо использовать в условии результаты-другой выборки. Например, если надо из отношения «Успеваемость» выбрать только студентов физико-математического факультета, пользуясь отношением «Студент», то команда select может выглядеть так:
select ФИО_студента
from Успеваемость
where ФИО_студента is in
(select Фамилия
from Студент
where Ф_т = «физмат»).
Здесь «is in» является представлением оператора принадлежности элемента множеству. Можно также использовать операторы «is not in» («не принадлежит множеству»), «contains» - содержит, «does not contains» - не содержит. Смысл выражения «A contains В» (А содержит В) тот же, что и выражения «В is in А» (В принадлежит множеству А). Помимо слов select, from, where в команде выборки можно использовать и другие служебные слова, например:
order by <атрибут> asc - определяет сортировку результата выборки
в порядке возрастания (asc) или убывания (desc)
значения атрибута;
group by <атрибут1> - группирует данные по значениям атрибута;
having set <атрибут2>
minus - операция вычитания множеств (данных выборок).
Помимо команды выборки select, язык SQL имеет команды, позволяющие обновлять данные (update), вставлять (insert) и удалять (delete). Например, если студенты переводятся со 2-го курса на третий, информацию можно обновить командой
update Студент
set Kypc=3
where Kypc=2.
Если атрибут «Семенов С.С.» сдал экзамен по информатике на «5» 15 января 1996 г.преподавателю Петрову П.П., то информация об этом может быть добавлена в таблицу «Успеваемость» командой
insert inio Успеваемость:
<«Семенов С.С.», «Информатика», 5,15/01/96, Петров П.П.>.
Оператор insert может быть использован для включения одной строки (как в этом примере) или произвольного числа строк, определенных списком кортежей, заключенных в скобки, или операций выборки select из какой-либо другой таблицы. Команда delete используется для удаления информации из таблицы. Например,
delete Успеваемость
where Оценка=2
позволяет удалить информацию о студентах, получивших 2 (в случае их отчисления).
Существенно расширяют возможности языка библиотечные функции, такие как count (подсчет), sum (суммирование), avg (среднее), max и min.
Например, подсчитать число студентов в таблице «Студент»: select count (*) from Студент.
СОВЕРШЕНСТВОВАНИЕ И РАЗВИТИЕ ВНУТРЕННЕЙ СТРУКТУРЫ ЭВМ
В предыдущем разделе была описана классическая структура ЭВМ, соответствующая вычислительным машинам первого и второго поколений. Естественно, что в результате бурного развития технологии производства средств вычислительной техники такая структура не могла не претерпеть определенных прогрессивных изменений.
Как отмечалось выше, появление третьего поколения ЭВМ было обусловлено переходом от транзисторов к интегральным микросхемам. Значительные успехи в миниатюризации электронных схем не просто способствовали уменьшению размеров базовых функциональных узлов ЭВМ, но и создали предпосылки для существенного роста быстродействия процессора. Возникло существенное противоречие между высокой скоростью обработки информации внутри машины и медленной работой устройств ввода-вывода, в большинстве своем содержащих механически движущиеся части. Процессор, руководивший работой внешних устройств, значительную часть времени был бы вынужден простаивать в ожидании
информации «из внешнего мира», что существенно снижало бы эффективность работы всей ЭВМ в целом. Для решения этой проблемы возникла тенденция к освобождению центрального процессора от функций обмена и к передаче их специальным электронным схемам управления работой внешних устройств. Такие схемы имели различные названия: каналы обмена, процессоры ввода-вывода, периферийные процессоры. Последнее время все чаще используется термин «контроллер внешнего устройства» (или просто контроллер).
Наличие интеллектуальных контроллеров внешних устройств стало важной отличительной чертой машин третьего и четвертого поколений.
Контроллер можно рассматривать как специализированный процессор, управляющий работой «вверенного ему» внешнего устройства по специальным встроенным программам обмена. Такой процессор имеет собственную систему команд. Например, контроллер накопителя на гибких магнитных дисках (дисковода) умеет позиционировать головку на нужную дорожку диска, читать или записывать сектор, форматировать дорожку и т.п. Результаты выполнения каждой операции заносятся во внутренние регистры памяти контроллера и могут быть в дальнейшем прочитаны центральным процессором.
Таким образом, наличие интеллектуальных внешних устройств может существенно изменять идеологию обмена. Центральный процессор при необходимости произвести обмен выдает задание на его осуществление контроллеру. Дальнейший обмен информацией может протекать под руководством контроллера без участия центрального процессора. Последний получает возможность «заниматься своим делом», т.е. выполнять программу дальше (если по данной задаче до завершения обмена ничего сделать нельзя, то можно в это время решать другую).
Перейдем теперь к обсуждению вопроса о внутренней структуре ЭВМ, содержащей интеллектуальные контроллеры, изображенной на рис. 4.11. Из рисунка видно, что для связи между отдельными функциональными узлами ЭВМ используется общая шина (часто ее называют магистралью). Шина состоит из трех частей:
• шина данных, по которой передается информация;
• шина адреса, определяющая, куда передаются данные;
• шина управления, регулирующая процесс обмена информацией.
Отметим, что существуют модели компьютеров, у которых шины данных и адреса для экономии объединены. У таких машин сначала на шину выставляется адрес, а затем через некоторое время данные; для какой именно цели используется шина в данный момент, определяется сигналами на шине управления.
Описанную схему легко пополнять новыми устройствами - это свойство называют открытостью архитектуры. Для пользователя открытая архитектура означает возможность свободно выбирать состав внешних устройств для своего компьютера, т.е. конфигурировать его в зависимости от круга решаемых задач.
На рис. 4.11 представлен новый по сравнению с рис. 4.10 вид памяти - видео-ОЗУ (видеопамять). Его появление связано с разработкой особого устройства вывода - дисплея. Основной частью дисплея служит электронно-лучевая трубка, которая отображает информацию примерно так же, как это происходит в телевизоре (к некоторым дешевым домашним моделям компьютеров просто подключается обычный телевизор). Очевидно, что дисплей, не имея механически движущихся частей, является «очень быстрым» устройством отображения информации.
Поэтому для ЭВМ третьего и четвертого поколений он является неотъемлемой частью (хотя впервые дисплей был реализован на некоторых ЭВМ второго поколения, например, на «МИР-2» - очень интересной во многих отношениях отечественной разработке).
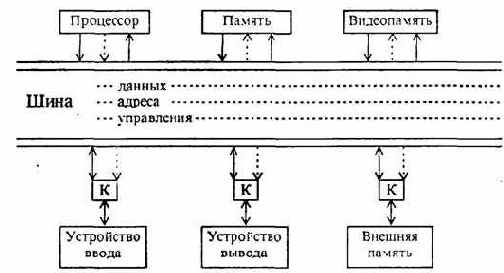
Рис. 4.11. Шинная архитектура ЭВМ
Для получения на экране монитора стабильной картинки ее надо где-то хранить. Для этого и существует видеопамять. Сначала содержимое видеопамяти формируется компьютером, а затем контроллер дисплея выводит изображение на экран. Объем видеопамяти существенно зависит от характера информации (текстовая или графическая) и от числа цветов изображения. Конструктивно она может быть выполнена как обычное ОЗУ или содержаться непосредственно в контроллере дисплея (именно поэтому на рис. 4.11 она показана пунктиром).
Остановимся еще на одной важной особенности структуры современных ЭВМ. Поскольку процессор теперь перестал быть центром конструкции, стало возможным реализовывать прямые связи между устройствами ЭВМ. На практике чаще всего используют передачу данных из внешних устройств в ОЗУ и наоборот. Режим, при котором внешнее устройство обменивается непосредственно с ОЗУ без участия центрального процессора, называется прямым доступом к памяти (ПДП). Для его реализации необходим специальный контроллер. Подчеркнем, что режим ПДП в машинах первого и второго поколений не существовал. Поэтому встречающаяся иногда схема ЭВМ, на которой данные из устройств ввода напрямую поступают в ОЗУ, не соответствует действительности: данные при отсутствии контроллера ПДП всегда сначала принимаются во внутренние регистры процессора и лишь затем в память.
При описании магистральной структуры мы упрощенно предполагали, что все устройства взаимодействуют через общую шину. С точки зрения архитектуры этого вполне достаточно. Упомянем все же, что на практике такая структура применяется только для ЭВМ с небольшим числом внешних устройств. При увеличении потоков информации между устройствами ЭВМ единственная магистраль перегружается, что существенно тормозит работу компьютера.
Поэтому в состав ЭВМ могут вводиться одна или несколько дополнительных шин. Например, одна шина может использоваться для обмена с памятью, вторая -для связи с «быстрыми», а третья - с «медленными» внешними устройствами. Отметим, что высокоскоростная шина данных ОЗУ обязательно требуется при наличии режима ПДП.
Завершая обсуждение особенностей внутренней структуры современных ЭВМ, укажем несколько характерных тенденций в ее развитии. Во-первых, постоянно расширяется и совершенствуется набор внешних устройств, что приводит, как описывалось выше, к усложнению системы связей между узлами ЭВМ. Во-вторых, вычислительные машины перестают быть однопроцессорными. Помимо центрального, в компьютере могут быть специализированные процессоры для вычисления с плавающей запятой (так называемые математические сопроцессоры), видеопроцессоры для ускорения вывода информации на экран дисплея и т.п. Развитие методов параллельных вычислений также вызывает к жизни вычислительные системы достаточно сложной структуры, в которых одна операция выполняется сразу несколькими процессорами. В-третьих, наметившееся стремление иметь быстродействующие машины не только для вычислений, но и для логического анализа информации, также может привести в ближайшие годы к серьезному пересмотру традиционной фон-неймановской архитектуры.
Еще одной особенностью развития современных ЭВМ является все ускоряющееся возрастание роли межкомпьютерных коммуникаций. Все большее количество компьютеров объединяются в сети и обрабатывают имеющуюся информацию совместно.
Таким образом, внутренняя структура вычислительной техники постоянно совершенствовалась и будет совершенствоваться. Вместе с тем, на данный момент подавляющее большинство существующих ЭВМ, несмотря на имеющиеся различия, по-прежнему состоит из одинаковых узлов и основано на общих принципах фон-неймановской архитектуры.
СОВМЕСТНОЕ РЕШЕНИЕ ЗАДАЧ
Совместное решение задач может оказаться новым, очень перспективным наполнением образовательной телекоммуникационной среды. Проекты могут быть основаны как на соревновании, так и на сотрудничестве, но примеры существующих проектов показывают, что учителя и учащиеся предпочитают сотрудничество.
Поиск информации. В on-line
проектах этого типа учащиеся должны использовать различные источники информации (электронные или бумажные) для решения задач. Им дается также ключ к решению. Известна географическая игра, в которой каждой из 20 участвующих групп учащихся дается однотипный набор информации о месте размещения их школы (широта, долгота, часовой пояс, численность населения, расстояние до столицы страны и т.д.). Координаторы игры перемешивают эти данные, а все учащиеся, используя справочную информацию (карты, атласы, географические справочники и т.д.) находят города и ставят им в соответствие информацию. Побеждает тот класс, который установит наиболее точное соответствие.
Электронное сочинение. Известны канадские проекты, в которых классы регулярно посылают сочинения в телеконференции. Другие учащиеся могут следить за работой такой электронной литературной секции. К проекту привлекаются профессиональные писатели, которые дают свои критические конструктивные заметки, делятся секретами мастерства, публикуют отрывки из своих произведений, над которыми они работают.
Одновременное выполнение заданий (в том числе конкурсы). В этом типе проектов учащимся, находящимся в разных местах, предлагают одинаковые задания для их выполнения. Затем происходит электронный обмен решениями. Получили известность архитектурные проекты такого, например, типа: «Какую самую высокую конструкцию вы сможете построить из спичек, чтобы она
1) могла нести на себе яйцо;
2) выдерживала, если на нее сильно подуют»?
При этом можно использовать только определенный клей. Яйцо должно быть сварено вкрутую и не очищено. Для оценки высылаются описание и рисунок.
Моделирование. On-line
моделирование - это такие телекоммуникационные проекты, которые требуют, возможно, наибольшей координации и поддержки,.
Однако эффективность обучения и увлеченность участников вполне оправдывают дополнительные затраты времени и усилий со стороны организаторов проекта. Среди успешных проектов on-line
моделирования назовем следующий.
Моделируется космическая программа «Шаттл». Школы всего мира играют различные роли в моделируемом полете космического корабля «Шаттл». Исследование включает маневр стыковки с другим «Шаттлом», управление полетом с наземного пульта управления, приземление в различных местах, наблюдение обсерватории солнечных возмущений и т.д. Координация и коммуникации между пультом управления «Шаттла» и другими школами осуществляется через распределенную конференцию на индивидуальных интерактивных сетевых системах. Электронная почта пересылается очень быстро, ежечасно публикуются отчеты, даже возможны электронные переговоры в реальном масштабе времени между пультом управления, астронавтами и вспомогательными подразделениями.
Известна прекрасная серия проектов моделирования международных событий и проблем, а также разрешения глобальных конфликтов. Упомянем проект IDEALS, основанный на моделировании учащимися деятельности и поведения высокопоставленных дипломатов, представляющих различные страны на международной конференции. Они должны, например, выработать текст договора об использовании океанских ресурсов или о будущем Антарктиды.
Социальные проекты. У граждан мира. живущих в конце XX века, не должно вызывать удивления то, что Internet
служит средой для гуманитарных межкультурных телекоммуникационных проектов, ориентированных на деятельность, в которых участвуют будущие руководители планеты - наши дети. Так, проект Planet использует консорциум шести связанных с Internet образовательных сетей, представители которых работают вместе над созданием проектов полезной, важной общественной деятельности, в которой дети впервые ощущают ответственность за решение глобальных проблем огромной важности.
В течение первых месяцев работы проекта Planet его участники писали в ООН петиции протеста против событий в Югославии, методом мозгового штурма разрешали политическую ситуацию в Сомали, планировали и искали источники финансирования орошения засушливых местностей Никарагуа.
Потенциал таких проектов для мультиднсциплинарного, устремленного в будущее, построенного на истинном сотрудничестве обучения несомненен.
К сожалению, большинство учебных компьютерных проектов, функционирующих в Internet и разработанных в США, в России неизвестно. Некоторую известность у нас получили учебные проекты сети KIDNET. Недостатком такого типа проектов является их ориентация на традиции, сложившиеся в образовании США: прагматичность, поверхностность, бессистемность. Такие проекты с трудом вписываются в предметную систему российского образования.
В ближайшие годы наилучшими перспективами обладают такие технологии обучения с использованием компьютерных телекоммуникаций, которые основаны на телекоммуникационной поддержке традиционных форм обучения и носят характер коллективно выполняемых под руководством педагога учебных проектов.
Такой характер имеют, в частности, получившие известность российские телекоммуникационные образовательные проекты, ориентированные на среднюю школу, такие как телекоммуникационная олимпиада по программированию. проведенная в Переславле-Залесском, олимпиада по физике, поддерживаемая в Красноярске, экономические игры МЭМ ( моделирование экономики и менеджмента ), методическое обеспечение которых выполняется в КУДИЦ (Москва), телекоммуникационные викторины (олимпиады) по ряду школьных предметов, экономическая бесконкурентная игра «экономические связи», проект изучения английского языка в переписке с американскими школьниками, методика которых разработана в Воронежском госпедуниверситете.
Очевидно, что на начальных этапах внедрения образовательных технологий на основе компьютерных телекоммуникаций могут возникнуть существенные трудности и помехи, среди которых
• недостаточно насыщенный компьютерный парк учебных учреждений и индивидуальных пользователей,
• недостаточное развитие компьютерных телекоммуникационных сетей в России, их нестабильность,
• недостаточная компьютерная грамотность и информационная культура населения, что создает дополнительные психологические барьеры в развитии телекоммуникационных методов обучения.
Однако главной проблемой развития телекоммуникационного обучения является создание новых методов и технологий обучения, отвечающих телекоммуникационной среде общения. В этой среде ярко проявляется то обстоятельство, что учащиеся не просто пассивно потребляют информацию, в процессе обучения они создают собственное понимание предметного содержания обучения. В настоящее время требуется коррекция устаревшей модели обучения, которая характеризовалась тем,что
• в центре технологии обучения - учитель;
• между учащимися идет негласное соревнование;
• учащиеся играют пассивную роль на занятиях;
• суть обучения - передача знаний (фактов).
На смену устаревшей модели должна прийти новая модель обучения, основанная на следующих положениях:
• в центре технологии обучения - учащийся;
• в основе учебной деятельности - сотрудничество;
• учащиеся играют активною роль в обучении;
• суть технологии - развитие способности к самообучению. Основные группы задач, решаемых с помощью сети, включают в себя
• поддержку учебной работы учащихся;
• обеспечение взаимодействия между педагогами, обмен педагогическим опытом и дидактическими материалами;
• обеспечение доступа всех участников учебно-воспитательного процесса к быстро растущим информационным фондам, хранящимся в централизованных информационных системах;
• информационное обеспечение решения задач управления.
Контрольные вопросы и задания
1. Каковы перспективы использования компьютерных сетей в образовании?
2. В чем состоит учебное значение электронной почты?
3. Что называется учебным телекоммуникационным проектом?
4. Охарактеризуйте основные виды учебного использования Internet.
5. С какими проблемами сталкивается учебное применение телекоммуникаций в России?
6. Предложите идею своего собственного телекоммуникационного проекта.
Дополнительная литература к главе 5
1. ВеттигД.
Novell Netware.-Киев: BHV, М., Бином, 1994. -
2. Вычислительные комплексы, системы и сети. /А.М.Ларионов , С.А.Майоров., Г.И.
Новиков: Учеб. для вузов.-Л.: Энергоатомиздат, 1987.
3. Глобальные сети: информация и средства доступа. - Пермь: ПГТУ, 1994.
4. Гольц Г.
Рабочие станции и информационные сети. - М.: Машиностроение, 1990.
5.Дансмур М., Дейвис Г. Операционная система UNIX и программирование на языке Си. М.: - Радио и связь, 1989.
6. Интернет. Всемирная компьютерная сеть. Практическое пособие и путеводитель. - М.: Синтез, 1995.
7. Каракозов С. Д. Введение в компьютерные сети. - Барнаул, БГПУ, 1996.
8. Компьютерные сети. Учебный курс Microsoft Corporation/ Пер. с англ. - М.: Издательский отдел «Русская Редакция» ТОО «Channel Trading Ltd.». - 1997.
9. Kpoл Эд. Все об INTERNET. Руководство и каталог. - Киев: BHV, 1995.
10.Ларионов A.M.. Майоров С. А.. Новиков Г. И.
Вычислительные комплексы, системы, сети. - М.: Энергоатомиздат, 1987.
11. Морозов В. К, Долганов А. В. Основы теории информационных сетей. - М.: Высшая школа, 1987.
12. Нанс Бэрри.
Компьютерные сети. - М.: БИНОМ, 1996.
13. Рассохин Д., Лебедев A.
World Wide Web - всемирная информационная паутина в сети Internet. - М.: МГУ, 1997.
14. Самойленко С. И. Сети ЭВМ. - М.: Наука, 1986.
15. Свириденко С. С. Современные информационные технологии. - М.: Радио и связь, 1989.
16. Сетевые средства Windows NT. - С.-Пб.: BHV-Санкт-Петербург, 1996.
17. Стандарты по локальным вычислительным сетям. Справочник / Под ред. С.И.Самойленко. - М.: Радио и связь, 1990.
18. Телекоммуникационная сеть в системе образования Пермской области. Информационно-справочное пособие. Часть 1. - Пермь: ОЦПИ, 1995.
19. Телекоммуникация и информатизация общества. Серия «Информация. Наука. Общество». - М.: ИНИОН, J990.
20. Уваров А. Ю.
Организация и проведение учебных телекоммуникационных проектов. - Барнаул, БГПУ, 1996.
21. Уваров А.Ю.
Учебные телекоммуникационные проекты в классе. - Барнаул, БГПУ, 1996.
22. Хромцов П.
Лабиринты Internet. - М.: Электронинформ. 1996
23. Электронная почта в системе MS-DOS. Официальное руководство компании Редком. 1995г.
24. Журнал «Компьютеруик-Москва», с 1995 г.
* СРЕДА ОБЪЕКТНОГО ВИЗУАЛЬНОГО ПРОГРАММИРОВАНИЯ DELPHI
* Раздел о Delphi написан Е.А.Ереминым.
Созданный в 1970 г. Н. Виртом, язык программирования Паскаль не оставался чем-то неизменным. Хотя основная его часть сохранилась прежней, появился целый ряд усовершенствований и дополнений, которые были направлены на облегчение программирования задач все возрастающей сложности. Например, типа данных string не было в первоначальной версии языка, в то время как представить без него современный Паскаль практически невозможно.
Позднее были добавлены более сложные конструкции: Н. Вирт предложил структуру программы из модулей unit, для возможности реализации объектного программирования был введен тип object. В результате возможности Паскаля значительно возросли и он по-прежнему мог удовлетворить запросы любого самого изощренного системного программиста. Известна, например, высокая оценка языка, которую дал в одной из своих книг знаменитый американский программист Питер Нортон: «Лично я пользуюсь и языком Паскаль, и языком Си. Мои популярные сервисные программы «Утилиты Нортона» были написаны на Паскале, а затем переписаны на Си. Мне нравятся оба эти языка. Я считаю, что сам по себе Паскаль лучше, в нем меньше возможностей допустить ошибку...».
С появлением графической среды Windows положение существенно изменилось. Конечно, реализовать программу с современным оконным интерфейсом на Паскале было возможно, но для этого требовалось немалое мастерство и много времени.
Чтобы исправить это положение, в 1996 г. фирма Borland, известная своими разработками в области реализации языков программирования, выпустила компилятор нового поколения Delphi. Прежде всего, это мощный компилятор языка Паскаль. дополненного рядом существенно новых возможностей для программирования в среде Windows. Но не только. Delphi - это система, имеющая интерфейс качественно нового типа, позволяющий при составлении текста программы видеть те графические объекты, для которых она пишется - так называемая, система визуального программирования.
Delphi является системой программирования очень высокого уровня.
Она берет на себя значительную часть работы по управлению компьютером, что делает возможным в простых случаях обходиться без особых знаний о деталях ее работы.
В отличие от традиционных систем программирования, Delphi даже «сама» пишет значительную часть текста программы: описания объектов, заголовки процедур и многое другое. Программисту остается только вписать необходимые строчки, определяющие индивидуальное поведение программы, которые система не в состоянии предугадать. Но даже здесь Delphi во многих случаях сама указывает место, где надо разместить эти строки.
Вершиной автоматизации процесса программирования являются, так называемые, эксперты. Эксперт - это диалоговое окно, которое помогает пользователю описать, что он хочет видеть в своей программе. Например, Эксперт проекта спрашивает, необходимо ли вам системное меню и какого из предложенных типов ваш проект. Проанализировав введенные ответы. Delphi пишет код программы на Паскале. Отметим, что эксперты могут быть созданы самим пользователем.
Чтобы составить себе некоторое представление о работе в Delphi, проследим за реализацией в системе конкретной пробной программы, рекомендованной в качестве первого шага освоения Delphi в одном из руководств. Опустим для простоты описание несущественных сейчас деталей, касающихся вида экрана и объектов управления на нем. Сосредоточим свое внимание на сути процесса создания программы в среде Delphi.
Еще до того, как программист успел что-то сделать, система при запуске уже выполнила значительную работу. Во-первых, она создала для будущей программы стандартное окно (в Delphi его принято называть формой). Во-вторых, уже сгенерирован текст программы довольно значительной длины, который необходим для порождения этой формы на экране.
Теперь попробуем что-нибудь сделать сами. Выберем из предлагаемого широкого ассортимента стандартных объектов наиболее простой - кнопку. Найдем ее изображение в верхней части экрана (в Delphi ее называют палитрой
компонентов) и щелкнем на нем мышкой.
СРЕДСТВА И МЕТОДЫ ОРГАНИЗАЦИИ ДИАЛОГА
В Бейсике
сильно развиты команды и функции ввода-вывода данных, позволяющие осуществлять диалог (интерактивный интерфейс) с пользователем.
Для осуществления клавиатурного управления программой, помимо уже известных операторов ввода INPUT и вывода PRINT, используют функцию INPUT$(n), возвращающею значение введенной символьной строки из п символов с ожиданием, функцию INKEYS, принимающею символьное значение нажатой клавиши без ожидания, функции STICK(n), STRIG(O), определяющие коды стрелок или направления джойстика (внешнего управляющего устройства для компьютерных игр и тренажеров).
Часто при разработке компьютерных программ необходимо использовать коды клавиш в ASCI-представлении. Следующая программа печатает код нажатой клавиши и может оказаться полезной при отсутствии под рукой таблицы ASCI кодов.
Программа 77 5 ' ************ коды символов ************
10 cls
20 f$ =
INPUT$(1)
30 PRINT "символ="; f$; "код="; ASC(f$)
40 PRINT 50 GOTO 20
Полную таблицу кодов символов можно получить и другим способом, см. программу 78.
Программа 78 5 ************ до коду печать символа **************
10 FOR i = 1 ТО 256
20 PRINT "код="; i, "символ="; CHR$(i)
30 a$ = INPUT$(1)
40 NEXT I
Функцию INPUTS часто используют для приостановки выполнения программы до нажатия любой клавиши:
п г$ = INPUTS(l): IF r$ = "" THEN n
В отличие от оператора INPLT ф\ нкцпя не ставит знак "?"и не высвечивает вводимые символы. Это свойство удобно использовать для защиты доступа к какой-либо информации. В следующем примере демонстрируется фрагмент проверки «своего» клиента с помощью пароля. Если при вводе четырехсимвольного пароля ("") трижды допущена ошибка, программа приостанавливает работу.
Программа 79 ;
5 ********** пароль *********'**
7 CLS
8 PRINT "нажми любую клавишу"
9 r$=INPUT$(l) : IF r$=""THEN 9
10 code$ = "1996" : k = О
20 INPUT "Имя"; а$
30 PRINT "Пароль"
40 р$ = INPUT$(4)
50 IF p$ = code$ THEN GOTO 80
60 k = k + 1 70 IF k < 3 THEN GOTO 30 ELSE PRINT "До свидания" : END
80 . PRINT 90 PRINT a$, "добро пожаловать"
100 END
С помощью строковой переменной INKEYS аналогично можно осуществлять временную задержку программы до нажатия любой клавиши:
n sS=INKEYS: IF sS=""THEN n
Ниже приведен пример назначения некоторых клавиш, управляющих процессом рисования точек (простейший графический редактор). Здесь код 27 (строка 20) означает клавишу Esc.
Программа 80
•^ i ********** простейший графический редактор ************ 5 SCREEN 2
6 х =
100: у = 100: h = 2
7 PSET (х, у)
10 g$ = INKEY$
20 IF g$ = CHR$(27) THEN 80
30 IF g$ = "A" OR g$ = "a " THEN х = х - h
40 IF g$ = "S" OR g$ = "s " THEN х = х + h
50 IF g$ = "Z" OR g$ = "z" THEN у = у + h
60 IF g$ = "W" OR g$ = "w" THEN у = у - h
70 GOTO 7
80 END
При разработке компьютерных программ полезно бывает использовать функциональные клавиши в качестве «горячих» (НОТ KEY). Назначение команд функциональным клавишам осуществляет оператор KEY. Его работу можно изучить по следующей демонстрационной программе.
Программа 81
5 ' ********** назначение функциональных клавиш ********
10 FOR i = 1 ТО 10
20 KEY i, "+ STR$(i)
30 NEXT i
40 KEY 30, "
50 KEY 31, "+ CHR$(13)
60 KEY LIST
70 KEY ON
80 r$ = INPUT$(1): IF r$ = ""THEN 80
СТРУКТУРА ПРОГРАММЫ НА СИ. ПОНЯТИЕ О ФУНКЦИЯХ
Программа на языке Си представляет собой набор последовательно описанных функций (процедуры и подпрограммы в языке Си считаются частным случаем функций). Каждая функция - самостоятельная единица программы, предназначенная для решения определенной задачи (или подзадачи). При описании она имеет следующий вид:
Тип_функцни Имя (<список аргументов>)
<описания аргументов>
{
<описания>
<операторы>
}
Отметим, что список аргументов может быть пустым (однако, скобки после имени функции сохраняются). В этом случае, естественно, нет и их описаний.
Имеется одна главная функция (с именем main), с которой начинается выполнение программы. Функции могут обращаться к другим функциям посредством конструкций вызова. Вызов функции используется при вычислении значения выражения. В результате вызова функция возвращает вычисленное значение, которое и является значением вызова функции. Попутно функция может преобразовывать значения своих аргументов. Такой результат вызова функции называется побочным эффектом.
В модуле, вызывающем данную функцию, тип возвращаемого ею значения должен быть описан (даже если это неопределенное значение) вместе с описанием переменных.
Пример. Пусть необходимо вывести на экран словосочетание «Простая функция без аргументов» 15 раз, используя функции.
Программа 97
#include<stdio.h>
main ()
(
int i,print() ;
for (i=l;i<=15;i++) print();
{
print() /* вызываемая функция без аргументов */
)
printf ("Простая функция без аргументов\n»);
}
Аргументы передаются по значению путем копирования в соответствующие (по порядку) параметры, указанные в определении функции. Соответствие аргументов и параметров по количеств) и типу не контролируется в языке Си. Такой контроль может быть выполнен с помощью дополнительных средств отладки.
Следует различать формальные аргументы, используемые при описании функций, и фактические, задаваемые при вызове функций. Формальный аргумент - переменная в вызываемой программе, а фактический аргумент - конкретное значение, присвоенное этой переменной вызывающей программой.
Фактический аргумент может быть константой, переменной или даже более сложным выражением. Независимо от типа фактического аргумента он вначале вычисляется, а затем его величина (в данном случае некоторое целое число) передается функции (см. программу 97). Можно задавать список аргументов, разделенных запятыми. Пример: программа 98, которая находит числа х, у, z, принадлежащие отрезку [1;20] и удовлетворяющие условию x^2 = у^2 + z^2.
Программа 98
#include<stdio.h>
main()
(
int х, у, z, zero() ;
char p, q, ch() ;
x=2; y=45; z=0;
q=’o’;
printf("х» "); zero(x);
printf("x+y+(x+y)^z= "); zero(x+y+(x+y)^z) ;
printf("q= "); ch(q);
}
int zero(u)
int u;
(
printf("%d\n",u);
)
char ch(u)
char u;
{
printf("%c\n",u);
)
Результат работы программы:
x=2
x+y+(x+y)^z= 94
q=0
Программа 99
#include<stdio.h>
main()
(
int x,y,z;
int zero();
printf("Следующие величины могут быть сторонами прямоугольного треугольника:\n");
for
(х=1;х<=20;х++)
for
(у=1;у<=20;у++)
for (z=l;z<=20;z++)
if (y*y+z*z==x*x)
zero(x,у,z);
}
int zero(f,g,h)
int f,g,h;
(
printf ("x= %d, y= %d, 2=%d\n",f,g,h);
)
Результат работы программы:
следующие величины могут быть сторонами прямоугольного треугольника
х= 5, у= 3, z= 4
х= 5, у= 4, z= 3 x= 10, y= 6, z= 8
x= 10, y=8, z=6 x= 13, y=5, z= 12
x= 13, y= 12, z= 5 x=
15, y= 9, z= 12
x= 15, y= 12, z=9 x=17, y=8, z=15 x= 17, y= 15,
z=8 x=20, y=12, z=16
x=20, y= 16, z= 12
Завершает выполнение данной функции и передает управление вызывающей функции оператор return; в главной функции main он же вызывает завершение выполнения всей программы. Оператор return может содержать любое выражение:
return (<выражение>);
Если выражение не пусто, то вычисляется его значение, которое и становится значением данного вызова функции.
Достижение «конца» функции (правой закрывающей фигурной скобки) эквивалентно выполнению оператора return без возвращаемого значения (т.е.
оператор return в конце функции может быть опущен).
Пример. Данная программа вычисляет факториал, если число меньше 8; если вводимое число больше или равно 8, то выводится сообщение «Очень большое число».
Программа 100
#include<stdio.h>
main()
{
int n, s() ;
printf("Введите число ");
scant("%d", &n) ;
if (n<8) printf(=%d", s(n)) ;
else printf("Очень большое число");
)
int s(x) /* определение функции с параметром */
int x;
{
int y,p=l;
for (y=x; y>0; y- ) p*=y;
return(p); /* Возвращает в основную программу значение р */
}
Результат работы программы:
1. Введите число 4
р=24
2.Введите число 9
Очень большое число
Пример:
предположим, что нужно вычислить x2 (для некоторого неотрицательного целого у) (очевидный способ реализации возведения в целочисленную степень -многократное умножение, но существует более эффективный алгоритм, приведенный ниже).
Программа 101
#include<stdio.h>
main()
(
int а, Ь, x, у, z;
int odd() ;
printf("\nВведите x, у через пробел: ");
scanf("%d %d", &х, &у); а=х; Ь=у; z=l;
while (b!=0)
if (odd(b))
{ z=z*a; b- -;}
else
( a=a*a; b=b/2;}
printf("\n%d", z);
}
int odd(t)
int t;
(
return((t%2==0)? 0:1);
)
Результат работы программы:
Введите x, у через пробел: 15 2
225
Если функции необходимо вернуть несколько значений, можно использовать два различных приема:
• применить глобальные переменные (в этом случае кроме изученных ранее характеристик переменных (имени, типа, значения), используется еще одна – класс памяти, см.ниже);
• применить переменные типа «указатель» в качестве аргументов функции. При вызове функции информация о переменной может передаваться функции в двух видах. Если мы используем форму обращения
function 1(х);
то происходит передача в функцию значения переменной х. Изменение этого значения в вызывающую функцию не возвращается.
Если мы используем форму обращения
function2(&x);
то происходит передача адреса переменной х. Теперь измененное значение переменной х может использоваться в вызывающей функции. Первая форма обращения требует, чтобы определение функции включало в себя формальный аргумент того же типа,что и х:
function l(num)
int num;
Вторая форма обращения требует, чтобы определение функции включало в себя формальный аргумент, являющийся указателем на один из объектов соответствующего типа:
function2(x)
int *x;
Обычно пользуются первой формой, если входное значение необходимо функции для некоторых вычислений или действий, и второй формой, если функция должна будет изменять значения переменных в вызывающей программе. Выше вторая форма вызова \же применялась при обращении к ф\нкции scanf(). Когда мы хотим ввести некоторое значение в переменную num, мы пишем scanf(''%d",&num). Данная функция читает значение, затем, используя адрес, который ей дается, помещает это значение в память.
Пример: пусть необходимо поменять местами заданные значения переменных х и у.
Программа 102
#include<stdio.h>
main()
{
int
х, у;
int interchange(); /* описание функции типа int */
x=l; y=3;
printf("Имели... x=l y=3\n") ;
interchange(&x, &y); /* обращение к функции (в данном случае передаются адреса переменных) */
printf("Получили... x=%d y=%d", х, у);
}
/* вызываемая функция */
int interchange(u, v)
int *u, *v;
(
int p;
p=*\i; *u=*v; *v=p;
}
Результат работы программы:
Имели х=1 у=3
Получили х=3 у=1
В этой программе в вызове функции interchange(&x,&y) вместо передачи значений х и у мы передаем их адреса. Это означает, что формальные аргументы и и v, имеющиеся в спецификации interchanage(u,v), при обращении будут заменены адресами и, следовательно, они должны быть описаны как указатели.
Поскольку х и у целого типа, u и v являются указателями на переменные целого типа, и мы вводим следующее описание:
int *u,*v; int p;
Оператор описания используется с целью резервирования памяти. Мы хотим поместить значение переменной х в переменную р, поэтому пишем: р=*u; Вспомните, что значение переменной u - это &х, поэтому переменная и ссылается на х. Это означает, что операция *u дает значение х, которое как раз нам и требуется. Мы не должны писать, например, так:
р = u; /* неправильно */
поскольку при этом происходит запоминание адреса переменной х, а не ее значения. Аналогично, оператор *u = *v соответствует оператору х = у.
Тип функции определяется типом возвращаемого ею значения, а не типом ее аргументов. Если указание типа отсутствует, то по умолчанию считается, что функция имеет тип int. Если значения функции не принадлежат типу int, то необходимо указать ее тип в двух местах.
1. Описать тип функции в ее определении:
char pun(ch,n) /* функция возвращает символ */
int n;
char ch;
2. Описать тип функции также в вызывающей программе. Описание функции должно быть проведено наряду с описаниями переменных программы; необходимо только указать скобки (но не аргументы) для идентификации данного объекта как функции.
main()
{
char rch,pun();
СТРУКТУРА СОВРЕМЕННОЙ ИНФОРМАТИКИ
Оставляя в стороне прикладные информационные технологии, опишем составные части «ядра» современной информатики. Каждая из этих частей может рассматриваться как относительно самостоятельная научная дисциплина; взаимоотношения между ними примерно такие же, как между алгеброй, геометрией и математическим анализом в классической математике - все они хоть и самостоятельные дисциплины, но, несомненно, части одной науки.
Теоретическая информатика
- часть информатики, включающая ряд математических разделов. Она опирается на математическую логику и включает такие разделы как теория алгоритмов и автоматов, теория информации и теория кодирования, теория формальных языков и грамматик, исследование операций и другие. Этот раздел информатики использует математические методы для общего изучения процессов обработки информации.
Вычислительная техника
- раздел, в котором разрабатываются общие принципы построения вычислительных систем. Речь идет не о технических деталях и электронных схемах (это лежит за пределами информатики как таковой), а о принципиальных решениях на уровне, так называемой, архитектуры вычислительных (компьютерных) систем, определяющей состав, назначение, функциональные возможности и принципы взаимодействия устройств. Примеры принципиальных, ставших классическими решений в этой области - неймановская архитектура компьютеров первых поколений, шинная архитектура ЭВМ старших поколений, архитектура параллельной (многопроцессорной) обработки информации.
Программирование - деятельность, связанная с разработкой систем программного обеспечения. Здесь отметим лишь основные разделы современного программирования: создание системного программного обеспечения и создание прикладного программного обеспечения. Среди системного - разработка новых языков программирования и компиляторов к ним, разработка интерфейсных систем (пример - общеизвестная операционная оболочка и система Windows). Среди прикладного программного обеспечения общего назначения самые популярные - система обработки текстов, электронные таблицы (табличные процессоры), системы управления базами данных.
В каждой области предметных приложений информатики существует множество специализированных прикладных программ более узкого назначения.
Информационные
системы - раздел информатики, связанный с решением вопросов по анализу потоков информации в различных сложных системах, их оптимизации, структурировании, принципах хранения и поиска информации. Информационно-справочные системы, информационно-поисковые системы, гигантские современные глобальные системы хранения и поиска информации (включая широко известный Internet) в последнее десятилетие XX века привлекают внимание все большего круга пользователей. Без теоретического обоснования принципиальных решений в океане информации можно просто захлебнуться. Известным примером решения проблемы на глобальном уровне может служить гипертекстовая поисковая система WWW, а на значительно более низком уровне - справочная система, к услугам которой мы прибегаем, набрав телефонный номер 09'.
Искусственный интеллект
- область информатики, в которой решаются сложнейшие проблемы, находящиеся на пересечении с психологией, физиологией, лингвистикой и другими науками. Как научить компьютер мыслить подобно человеку? - Поскольку мы далеко не все знаем о том, как мыслит человек, исследования по искусственному интеллекту, несмотря на полувековую историю, все еще не привели к решению ряда принципиальных проблем. Основные направления разработок, относящихся к этой области - моделирование рассуждений, компьютерная лингвистика, машинный перевод, создание экспертных систем, распознавание образов и другие. От успехов работ в области искусственного интеллекта зависит, в частности, решение такой важнейшей прикладной проблемы как создание интеллектуальных интерфейсных систем взаимодействия человека с компьютером, благодаря которым это взаимодействие будет походить на межчеловеческое и станет более эффективным.
СТРУКТУРА СОВРЕМЕННОЙ СИСТЕМЫ РЕШЕНИЯ ПРИКЛАДНЫХ ЗАДАЧ
Разработки систем искусственного интеллекта шли сначала по пути моделирования общих интеллектуальных функций индивидуального сознания. Однако, развитие вычислительной техники и программного обеспечения в 90-х годах опровергает прогнозы предыдущих десятилетий о скором переходе к ЭВМ 5-го поколения. Интеллектуальные функции основной массы программных систем общения на естественном языке пока не находят широкого внедрения в промышленных масштабах.
Характерную инфляцию претерпело такое понятие, как «новая информационная технология». Первоначально это понятие означало интеллектуальный интерфейс к базе данных, позволяющий прикладным пользователям общаться с ней непосредственно на естественном языке. Ныне под «новыми информационными технологиями» понимают просто технологии, существенно использующие вычислительную технику в обработке информации, в том числе основанные на применении текстовых и табличных процессоров, а также информационных систем.
Столкнувшись с непреодолимыми проблемами, разработчики систем, обладающих «общим» искусственным интеллектом, пошли по пути все большей и большей специализации, вначале по направлению к экспертным системам, затем - к отдельным очень специфичным интеллектуальным функциям, встроенным в инструментальные программные средства, не считавшиеся до настоящего времени сферой разработок по искусственному интеллекту. Например, такие системы сейчас часто обладают возможностями аналитических математических вычислений, перевода технических и деловых текстов, распознавания текста при вводе сканером, синтаксического анализа фраз и предложений, самонастраиваемостью и т.д.
Парадигма исследований и разработок в области искусственного интеллекта постепенно пересматривается. По-видимому, возможности скорого развития программных систем, моделирующих интеллектуальные функции индивидуального сознания, в значительной мере исчерпаны. Необходимо обратить внимание на новые возможности, которые открывают в отношении общественного сознания информационные системы и сети. Развитие вычислительных систем и сетей ведет» по-видимому, к созданию нового типа общественного сознания, в которое информационные средства будут органично встроены как технологическая среда обработки и передачи информации. После этого человечество получит именно гибридный человеко-машинный интеллект не столько в масштабе индивидуального сознания, сколько в сфере социальной практики.
СТРУКТУРА УЧЕБНОГО МИКРОКОМПЬЮТЕРА
В состав учебного микрокомпьютера входят следующие устройства (рис. 4.16):
центральный процессор, память двух видов (ОЗУ и ПЗУ), а также два наиболее важных внешних устройства (клавиатура для ввода информации и дисплей для вывода; оба устройства, как принято в современных ЭВМ, подключены через обеспечивающие согласование контроллеры).
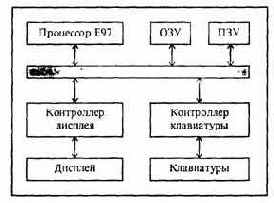
Рис. 4.16. Схема устройства учебного компьютера «Е97»
Главным блоком компьютера служит 16-разрядный процессор «Е97», способный работать как с двухбайтовыми словами, так и с отдельными байтами. Таким образом, он может оперировать с данными разной длины. Познакомившись с тем, как «Е97» обрабатывает разные типы информации, читатель легко сможет в будущем обобщить логику «один байт или много» на случай большей разрядности процессора.
В процессоре имеются внутренние регистры памяти, при помощи которых реализован метод косвенной адресации к ОЗУ. Очевидно, что полное 16-разрядяое адресное пространство «Е97» позволяет напрямую адресовать до 64 кбайт памяти; для учебной ЭВМ это более чем достаточно. Поэтому реально существующей памяти будут соответствовать лишь некоторые диапазоны адресов (рис. 4.17). Для первой программной реализации модели «Е97» приняты следующие значения констант: LoROM = 4000, HiROM =4180.
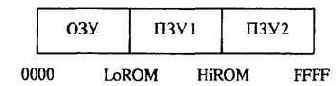
Рис. 4.17. Структура памяти микрокомпьютера «Е97» (LoROM - нижняя граница ПЗУ 1. HiROM-верхняя граница ПЗУ 1, совпадающая с началом ПЗУ 2)
В «Е97», как и в реальном компьютере, существует память двух видов -оперативная (ОЗУ) и постоянная (ПЗУ) В первой хранится текущая информация (т.е. программа и данные) по решаемон задаче, причем она может как считываться, так и записываться. Во второй, предназначенной только для считывания, содержатся разработанные при проектировании ЭВМ подпрограммы наиболее важных и часто используемых действий, среди которых важное место занимают алгоритмы обмена с внешними устройствами.
Видеопамять в «Е97» размещается в контроллере дисплея; для простоты модели будем считать, что видеопамять не входит в адресное пространство процессора.
Доступ к видео-ОЗУ осуществляется путем обращения к внешнему устройству.
Как уже отмечалось, минимальной адресуемой ячейкой памяти в современных ЭВМ является байт. Все байты в памяти «Е97» пронумерованы и их 16-разрядные номера находятся в пределах от 0000 до FFFF. Реальные адреса должны попадать в выделенные на рис. 4.17 области. При обращении к любому другому адресу происходит аварийное прекращение выполнения программы.
Байты в памяти могут объединяться в слова, которые для данного компьютера состоят из двух соседних байтов (у современных процессоров обычно из четырех, но для понимания основных принципов это не очень существенно). По традиции .примем, что слово адресуется наименьшим из номеров байтов, причем этот адрес соответствует младшему байту слова. Для удобства изображения содержимого ОЗУ на экране дисплея будем считать, что адрес слова всегда является четным
Для наглядности проиллюстрируем все эти важные положения примером (рис. 4.18). Слово с адресом 40 имеет значение FFOO, а слово с адресом 42 - 1234; адреса 41 и 43 для слов запрещены. Обратите внимание на то, что байт 40 имеет нулевое значение, а байт с адресом 41 - значение FF. Иначе говоря, байты слова хранятся в памяти «задом наперед» - сначала младший, а затем старший. Именно так хранится слово в большинстве компьютеров.
Рассмотрим теперь роль ПЗУ. Его наличие дает целый ряд преимуществ, важнейшими из которых являются следующие.
|
40 |
41 |
42 |
43 |
41 |
FF |
00 |
40 |
|
|
00 |
FF |
34 |
12 |
43 |
12 |
34 |
42 |
|
|
Представление в байтах |
Представление в словах |
Во-первых, в современных ЭВМ не всякое элементарное действие реализуется в виде команды процессора - многие из них выполняются по программе. В «Е97», например, по программе происходит нахождение остатка от деления, вычисление модуля, перевод целого числа из двоичной системы в десятичную. Наличие таких подпрограмм освобождает модель от необходимости вводить в систему команд учебного процессора разные нестандартные и несуществующие в реальных процессорах команды типа «вывод числа на экран в десятичной форме» и ей подобные.
Во-вторых, наличие ПЗУ позволяет не конкретизировать алгоритм работы с внешними устройствами на уровне системы команд процессора, а перенести их в ПЗУ (именно так делается и в настоящих компьютерах). ПЗУ такого рода носит специальное название BIOS (от английского Basic Input Output System - базовая система ввода-вывода) и обслуживает конкретные типы внешних устройств, входящих в состав машины BIOS имеет стандартные точки входа, к которым и обращается все программное обеспечение при необходимости произвести обмен информации с внешним устройством.
Завершая обсуждение ПЗУ, отметим еще одну деталь. В данной учебной ЭВМ оно условно делится на две части, названные на рис. 4.17 ПЗУ1 и ПЗУ2. ПЗУ1 доступно для изучения и представляет собой настоящие программы в кодах процессора «Е97». Другая часть долговременной памяти - ПЗУ2 - напротив, «скрыта» от просмотра. Определены лишь входные точки и их назначение; в основном это операции ввода. Деление на ПЗУ1 и ПЗУ2 является чисто техническим приемом и не имеет никаких аналогий в реальных ЭВМ (наличие «закрытого» ПЗУ2 просто позволяет легче и быстрее осуществить программный имитатор учебного микрокомпьютера).
Перейдем к рассмотрению контроллеров внешних устройств В учебном микрокомпьютере они фигурируют в виде портов ввода-вывода Каждому из устройств соответствует два таких порта:
регистр данных и регистр состояния. Через первый происходит обмен информацией, а второй позволяет этот обмен синхронизировать. Если в знаковый (старший) бит младшего байта регистра состояния записана единица, то это означает, что устройство к обмена готово.
Отметим, что контроллеры современных периферийных устройств имеют обычно более двух портов. Например, в IBM-совместимых компьютерах для работы со стандартным печатающим устройством используется три порта - к уже названным добавляется регистр управления. Ничего принципиально нового наличие дополнительных портов не вносит.
Такова внутренняя структура учебного микрокомпьютера. Рассмотрим теперь устройство самого процессора, каким он видится программисту.
«Е97» состоит из семи 16-разрядных регистров. 4 регистра общего назначения RO - R3, счетчика адреса команд PC (Program Counter), указателя стека SP (Stack Pointer) и регистра состояния процессора PS (Processor Status), в котором мы будем использовать только два младших бита N и Z. «Поведение» этих управляющих битов согласно общепринятым закономерностям следующее:
N = 0 - результат ? 0, N = 1 - результат < 0,
Z = 0 - результат ? 0, Z = 1 - результат = 0.
Здесь «результат» означает результат последней из выполненных арифметических операций. Все эти объекты изображены на рис. 4.19.
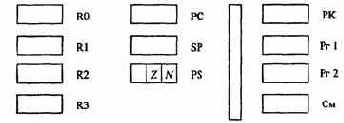
Рис. 4.19, Внутреннее устройство учебного процессора «Е97»
Кроме уже названных, в «Е97» имеется ряд внутренних регистров, которые процессор использует при исполнении операций. Это регистр команд РК, предназначенный для хранения кода исполняемой в данный момент команды; регистры операндов Рг1 и Рг2, куда считываются исходные данные; сумматор См, в котором производится требуемое в команде действие и получается результат. Мы не можем непосредственно изменять содержимое этих «служебных» регистров, но в данном учебном компьютере они доступны для наблюдения. Вертикальная заштрихованная полоса на рисунке разделяет программно-доступные (слева) и программно-недоступные (справа) регистры.
СТРУКТУРИРОВАННЫЕ ТИПЫ ДАННЫХ
Описанные выше типы данных называют простыми. Основной признак, по которому можно определить величину простого типа, таков: одно имя - одно значение.
Значительно большие возможности заключают в себе структурированные данные, определяемые разработчиком программы (в пределах возможностей используемого им языка программирования), К структурированию данных разработчика программы толкает как логика прикладной задачи, так и чисто утилитарное соображение: при наличии в задаче большого количества входных и выходных данных отдельное именование каждого из них может оказаться практически невозможным.
Разумеется, действия разработчика алгоритма и программы ограничены возможностями того языка программирования, на который он ориентируется. В разных языках возможности структуризации переменных на уровне сложных структур не совпадают, но многие структуры давно стали традиционными и реализованы в большинстве практически используемых языков программирования.
Структурированные типы данных классифицируют по следующим основным признакам: однородная - неоднородная, упорядоченная - неупорядоченная, прямой доступ - последовательный доступ, статическая - динамическая. Эти признаки противостоят друг другу лишь внутри пары, а вне этого могут сочетаться.
Если все элементы, образующие структуру, однотипны (например - целые числа или символы), то структура является однородной; если же в ней «перепутаны» элементы разной природы (например, числа чередуются с символами), то неоднородной.
Структуру называют
упорядоченной, если, между ее элементами определен порядок следования. Примером упорядоченной математической структуры служит числовая последовательность, в которой у каждого элемента (кроме первого) есть предыдущий и последующий. Наличие индекса в записи элементов структуры уже указывает на ее упорядоченность (хотя индекс для этого не является обязательным признаком).
По способу доступа упорядоченные структуры бывают прямого и последовательного доступа. При прямом доступе каждый элемент структуры доступен пользователю в любой момент независимо от других элементов.
Глядя на линейную таблицу чисел мы можем списать или заменить сразу, допустим, десятый элемент. Однако, если эта таблица не на бумаге, а, скажем, каким-то образом записана на магнитофонную ленту, то сразу десятое число нам недоступно - надо сначала извлечь девять предшествующих. В последнем случае мы имеем дело с последовательным доступом.
Если у структуры размер (длина, количество элементов) не может быть изменен «на ходу», а фиксирован заранее, то такую структуру называют статической. Программные средства информатики иногда позволяют не фиксировать размер структуры, а устанавливать его по ходу решения задачи и менять при необходимости, что бывает очень удобно. Такую структуру называют динамической. Например, при описании закономерностей движения очереди в магазине мы не знаем заранее, сколько человек в ней будет в тот или иной момент, и соответствующую структуру данных (например, список фамилий участников очереди) лучше представлять динамической.
Массивы
Самым традиционным и широко известным из структурированных типов данных является массив
(иначе называемый регулярным типом) - однородная упорядоченная статическая структура прямого доступа.
Массивом называют однородный набор величин одного и того же типа, называемых компонентами массива, объединенных одним общим именем (идентификатором) и идентифицируемых (адресуемых) вычисляемым индексом.
Это определение подчеркивает, что все однотипные компоненты массива имеют одно и то же имя, но различаются по индексам, которые могут иметь характер целых чисел из некоторого диапазона, литер, перечисленных констант. Индексы позволяют адресовать компоненты массива, т.е. получить доступ в произвольный момент времени к любой из них как к одиночной переменной (рис. 1.32). Обычный прием работы с массивом - выборочное изменение отдельных его компоневт.
Вычисляемые индексы позволяют использовать единое обозначение элементов массива для описания массовых однотипных операций в циклических конструкциях программ.
Важной особенностью массива является его статичность. Массив должен быть описан в программе (т.е. определены тип и число компонент) и его характеристики не могут быть изменены в ходе выполнения программы.
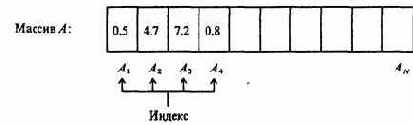
Рис. 1.32. Одномерный массив - набор элементов (компонентов)
Компонентами массива могут быть не только простейшие данные, но и структурные, в том числе массивы. В этом случае мы получаем массив массивов - многомерный массив. Для индексации элементарных компонент в этом случае может потребоваться два, три и более индексов.
В некоторых системах программирования существуют специальные виды массивов. Например, массив литер (символов) определяется как строка.
Данные, хранящиеся в массивах, находятся в оперативной памяти компьютера. Это, с одной стороны, ускоряет доступ к ним в ходе решения задачи, а с другой -налагает ограничения на объем возможной информации, организованной в виде массивов. Не следует поэтому, без крайней необходимости, создавать новые массивы для перемещения данных из уже существующих массивов.
Рассмотрим в качестве примера задачу сортировки набора некоторых данных, для которых имеют смысл отношения «больше» или «меньше». Представьте себе, что надо карточки в картотеке разместить в порядке возрастания записанных на них чисел. Используем для сортировки набора чисел (т.е. записи их в порядке возрастания) одномерный (линейный) массив. Дадим ему имя А,
тогда a1, a2, a3,..., аn - компоненты массива.
Существует огромное число методов сортировки массивов. Рассмотрим один из самых простых (но не самых быстрых) - метод выбора.
В начале процесса имеем заполненный числами массив (неотсортированный). Процесс сортировки строится по индукции. Допустим, мы уже отсортировали часть массива и имеем упорядоченную последовательность
a1 < a2
< … < ai-l
и оставшуюся неотсортированной последовательность
ai, ai+1,… aN.
При каждом шаге, начиная с i = 1, из неотсортированной части последовательности извлекается наименьший элемент х = ai, и меняется местами с i-м элементом.
Затем этот процесс повторяется для i = 2, i = 3 и т.д., до тех пор пока не останется один, самый большой элемент.
Этот алгоритм потребует многократного нахождения наименьшего элемента массива. Этот «вспомогательный» алгоритм поиска наименьшего среди аi, ... , аN может быть следующим:
1) фиксируется в качестве значения вспомогательной переменной т первый слева элемент массива: т = аi (в конце процесса т будет иметь значение наименьшего элемента);
2) выполняется сравнение т с элементом массива aj, (начиная с номера j = i + 1) и, если aj < т, то т заменяется на аj;
3) далее выполняется сравнение т с очередным элементом массива, т.е. j увеличивается на единицу и шаги 2, 3 выполняются снова, до тех пор пока у не достигнет максимального значения индекса элемента массива.
После выполнения этих предписаний переменная т будет соответствовать наименьшему элементу массива.
Двумерный массив визуально представляется плоской таблицей, табл. 1.10. При наличии одного имени (идентификатора) для всех компонентов каждый из них фиксируется значениями двух индексов, указывающих номер строки и номер столбца, на пересечении которых находится эта компонента.
Рассмотрим пример обработки данных, хранящихся в двумерном массиве. Допустим, что на некоторой территории (например, страны) «квадратно-гнездовым» способом расставлены температурные датчики, и их показания обраны в одном центре (что вполне близко к реальной деятельности метеослужбы). Тогда в таблицу - двумерный массив - попадут значения температуры tij
в сответствующих точках. Требуется, просматривая таблицу построчно, найти те точки (т.е. индексы узлов), между которыми температура принимает некоторое заданное значение Т.
Таблица 1.10 Графический образ двумерного массива
 |
1 |
2 |
3 |
4 |
… |
|
1 |
a11 |
a12 |
a13 |
a14 |
… |
|
2 |
a21 |
a22 |
a23 |
a24 |
… |
|
3 |
a31 |
a32 |
a33 |
a34 |
… |
|
4 |
a41 |
a42 |
a43 |
a44 |
… |
|
… |
… |
… |
… |
... |
… |
Пусть в таблице п
строк и т столбцов. Вспомогательным алгоритмом в данной задаче может быть алгоритм поиска нужных узлов в одной строке. Пусть эта строка имеет номер k. Алгоритмы записаны без комментариев для самостоятельного разбора.
Вспомогательный алгоритм (k):
1) положить j = 1;
2) если tk,j < T < tk.j+1, то см. п. 2;
3) увеличить j на 1,
4) если j < m, то вернуться к п. 2;
5) задача решена, ответ: (k,j), (k,j + 1);
6)конец.
Основной алгоритм:
1) положить k= 1;
2) выполнить вспомогательный алгоритм (K);
3) увеличить k
на 1;
4) если k > n,
то вернуться к п.2;
5)конец.
Записи, множества, файлы
Обобщением массива является комбинированный тип данных - запись, являющаяся неоднородной упорядоченной статической структурой прямого доступа. Запись есть набор именованных компонент - полей (часто разного типа), объединенных одним общим именем и идентифицируемых (адресуемых) с помощью как имени записи, так и имен полей, рис. 1.33.
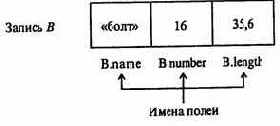
Рис. 1.33. Иллюстрация «записи».
Запись В
состоит из трех полей, имеющих последовательно типы «текст», «целое число», «вещественное число»: 1-е поле - название детали, 2-е - условный номер по каталогу, 3-е - длина. При работе с одной единственной записью (что бывает нечасто), имя поля можно использовать как обычную переменную, т.е. можно изменять значение поля с помощью операции присваивания или любых других операций, доступных над величинами данного типа. Если же данная запись - лишь часть набора данных, то имя поля состоит из двух частей и называется составным именем поля (на рис. 1.33 составные имена В. name, В. number, В. length).
Для облегчения работы с полями в различных языках программирования существуют средства, облегчающие их адресацию.
И записи, и массивы обладают одним общим свойством - произвольным доступом к компонентам. Записи более универсальны в том смысле, что для них не требуется идентичности типов их компонент. Массивы обеспечивают большую гибкость -индексы их компонент можно вычислять в отличие от имен полей записей.
Существенно иные возможности дает структура данных, моделирующая свойства математического объекта - множества.
Над множеством могут быть выполнены следующие операции:
1) объединение множеств (операция сложения '+');
2) пересечение множеств (операция умножения '*');
3) теоретико-множественная разность (вычитание множеств '-');
4) проверка принадлежности элемента множеству.
Различия между множеством и массивом очень существенны: размер множества заранее не оговаривается (хотя и ограничен компьютерной реализацией, например, 255), не существует иного способа доступа к элементам множества, кроме как проверкой принадлежности множеству.
Более сложной, чем рассмотренные выше из предусмотренных в современных системах программирования структур данных, является очередь (файл).
Понятие «файл» при всей своей привычности употребляется в информатике в нескольких не совсем совпадающих смыслах. Здесь мы остановимся лишь на представлении о файле как однородной упорядоченной динамической структуре последовательного доступа - очереди.
Очередь есть линейно упорядоченный набор следующих друг за другом компонент, доступ к которым происходит по следующим правилам:
1) новые компоненты могут добавляться лишь в хвост очереди;
2) значения компонент могут читаться (извлекаться) лишь в порядке следования компонент от головы к хвосту очереди.
Размер очереди заранее не оговаривается и теоретически может считаться бесконечным. Для запоминания (хранения) компонент очереди часто используют внешние запоминающие устройства большой емкости - магнитные диски и ленты. Отсюда другое название очереди - файл (по английски это слово имеет ряд значений, в том числе «картотека», «шеренга», «очередь»).
Исторически слово «файл» стало впервые применяться в информатике для обозначения последовательного набора каких-либо данных или команд (программа), хранящихся на внешнем запоминающем устройстве. Несколько позже были осознаны абстрактные, не зависящие от магнитных дисков и лент, свойства очереди как структуры данных, полезные при решении многих задач обработки - информации.
Такой принцип извлечения и добавления компонент к очереди часто; называется «первым вошел - первым вышел» (английская аббревиатура - «FIFO»), рис. 1.34.
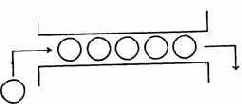
Рис. 1.34. Иллюстрация «очереди»
В языках программирования существуют и такие разновидности файлов, которые не подчиняются условию последовательности доступа к его компонентам (так называемые, файлы прямого доступа). Они уже не являются очередями.
Суперпозиция структур данных
Из рассмотренных структур данных можно создавать различные суперпозиции (вопрос о допустимости той или иной суперпозиции в конкретном языке программирования следует искать в его описании).
Рассмотрим в качестве примера такую часто используемую суперпозицию как файл записей - обычную, например, при создании баз данных. Итак, имеется файл по имени F, содержащий некоторое количество таких записей, как на рис. 1.30. Составим алгоритм подсчета количества болтов, у которых длина (length) заключена в пределах от 3 до 40:
1) положить k = 0 (в конце работы k - число искомых болтов);
2) прочесть первую запись из файла;
3) если В.name = 'болт' и 30 < B.lenght < 40, то увеличить k на 1;
4) если файл уже опустел, то идти к п. 7, иначе - к п. 5;
5) прочесть следующую запись из файла;
6) идти к п.З;
7) конец работы; k - число
искомых болтов.
Стек
Существует (и часто используется) и другая структура данных, в которой тот элемент, который первый в нее помещался, выходит последним и, наоборот, тот, который последним входит, выходит первым (английская аббревиатура «LIFO»). Такая структура получила название стек
(или магазин - по сходству с магазином стрелкового оружия), рис. 1.35.
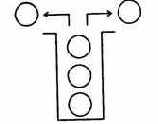
Рис. 1 35. Иллюстрация «стека»
Стеки и принцип LIFO находят очень широкое применение в информатике. Рассмотрим в качестве примера использование стека при вычислении значения арифметического выражения.
Вычисление значения выражения требует соблюдения старшинства операций. Операции по старшинству при вычислении значений математических выражений располагаются в следующем порядке: вычисление значений функций (включая возведения в степень), умножения и деления, сложения и вычитания.
Изменить такой «естественный» порядок операций можно с помощью скобок.
Например, вычисление известного из школьного курса математики выражения b2-
4*а*с включает предварительное установление порядка выполнения операций:
14 2 3
b2 – 4*a*c
Для этого выражение просматривают несколько раз. Выполнение каждой операции дает некоторое число, которое приходится записывать отдельно от выражения, запоминая тот фрагмент выражения, для которого число является значением.
Сейчас рассмотрим экономный алгоритм вычисления значения выражения, использующий два магазина для перестановки элементов выражения (с учетом старшинства операций) и для хранения промежуточных результатов. Магазины обозначим M1 и М2, в M1
будут попадать знаки операций, в М2
- числа, участвующие в записи выражения, значения переменных и все промежуточные числовые значения.
Ограничимся выражениями, состоящими только из чисел и переменных без индекса, связанных знаками операций, *, /, +, -. Знак «минус» будет знаком лишь двухместной операции вычитания, выражения типа « - а + I» исключаются из рассмотрения. От этих ограничений можно было бы и отказаться, но это удлинило бы изложение. Пока предположим также, что в выражении нет скобок.
Опишем алгоритм вычисления. Исходное выражение читается слева направо; если прочитано число, то оно заносится в M2, если переменная - в М2 заносится ее значение; если же прочитан знак операции, то необходимо различать несколько случаев.
1) М1 пуст; прочитанный знак помещается на вершину М1.
2) прочитанный знак помещается на вершину M1, если он обозначает операцию, которая старше и поэтому должна выполняться до операции, знак которой был расположен на вершине М1.
3) если операции равноправны или если та, знак которой только что прочитан в выражении, должна выполняться позднее, необходимо применить операцию, знак которой расположен на вершине M1, к двум верхним числам из М2 (число на вершине - второй операнд, число под ним - первый); знак операции на вершине M1 удаляется из M1,
вместо двух верхних чисел в M2
помещается результат выполнения над ними операции.
В некоторый момент в исходном выражении не остается символов. Если пуст и M1,
то вычисление окончено, результат находится в M2; в противном случае знаки операции извлекаются по очереди из M1
и соответствующие операции применяются к числам из M2.
Рассмотрим вычисление выражения b2 - 4*а*с; значения переменных а, b, с обозначим А, В, С. Знак возведения в степень обозначим, как часто делается, стрелкой вверх.


Про знак операции говорят, что он имеет более высокий приоритет в сравнении с другим знаком, если обозначаемая им операция старше. В других случаях говорят о равных приоритетах или более низком приоритете. Рассмотренные знаки операций распадаются на группы равных по приоритету:
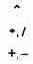
Группы упорядочены по убыванию приоритета.
Теперь дадим правило работы со скобками. Левая скобка заносится в M1
сразу после прочтения. Прочтение правой скобки влечет выполнение всех операций, знаки которых находятся в Mi
выше левой скобки; после выполнения этих операций обе скобки уничтожаются. Вот что будет происходить при выполнении (а + b) * с:
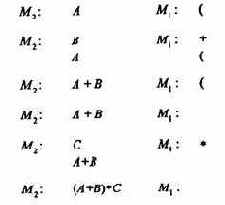
Иерархическая организация данных
Во всех рассмотренных выше структурах отдельные элементы (компоненты, поля, составляющие) структуры были формально равноправны. Существует, однако, широкий круг задач, в которых одни данные естественным образом «подвязаны» к другим. В этом случае возникает соподчиненная (иерархическая) структура данных. Ограничимся конкретным примером. Представим себе генеалогическое дерево, корень которого - имя человека, на следующем уровне - имена его родителей, еще на следующем - имена родителей родителей и т.д. Такая структура называется двоичным деревом, рис. 1.36.
Рис. 1.36. Структура типа «двоичное дерево»;
пара ближайших по горизонтали кружков -мужское и женское имя
Как структурировать эти данные (имена)? Для помещения их в текстовый массив и запись трудно придумать логически оправданный порядок следования.Самое разумное - создать динамическую структуру типа той, что изображена на рис. 1.36. современные языки программирования позволяют это делать и обрабатывать такие структуры с высокой эффективностью.
СТРУКТУРНЫЙ ПОДХОД
С появлением массовых ЭВМ 3-го поколения устаревшая технология программирования оказалась основным фактором, сдерживающим развитие и распространение компьютерных (информационных) технологий, что подтолкнуло ведущие в этой сфере деятельности фирмы, в первую очередь IBM, к разработке новых методологий программирования. Появившийся в начале 1970-х годов новый подход к разработке алгоритмов получил название структурного.
С появлением структурного программирования описанные выше трудности были во многом преодолены. В основе технологических принципов структурного программирования лежит утверждение о том, что логическая структура программы может быть выражена комбинацией трех базовых структур: следования, ветвления и цикла (это содержание теоремы Бема-Якопини).
Следование - самая важная из структур. Она означает, что действия могут быть выполнены друг за другом, рис. 1.19:

Рис. 1.19. Структура «следование»
Эти прямоугольники могут представлять как одну единственную команду, так и множество операторов, необходимых для выполнения сложной обработки данных.
Ветвление - это структура, обеспечивающая выбор между двумя альтернативами. Выполняется проверка, а затем выбирается один из путей (рис. 1.20).
Эта структура называется также «ЕСЛИ - ТО - ИНАЧЕ», или «развилка». Каждый из путей (ТО или ИНАЧЕ) ведет к общей точке слияния, так что выполнение программы продолжается независимо от того, какой путь был выбран.
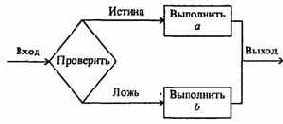
Рис. 1.20. Структура «ветвление»
Может оказаться, что для одного из результатов проверки ничего предпринимать не надо. В этом случае можно применять только один обрабатывающий блок, рис.1.21:
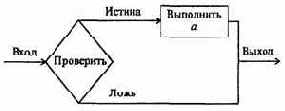
Рис. 1.21. Структура «неполное ветвление»
Цикл (или повторение) предусматривает повторное выполнение некоторого Набора команд программы. Если бы циклы не существовали, вряд ли занятие программированием было бы оправданным: циклы позволяют записать длинные последовательности операций обработки данных с помощью небольшого числа повторяющихся команд.
Разновидности цикла изображены на рис. 1.22 и рис. 1.23.
Цикл начинается с проверки логического выражения. Если оно истинно, то выполняется «a», затем все повторяется снова, пока логическое выражение сохраняет значение «истина». Как только оно становится ложным, выполнение операций «а» прекращается и управление передается по программе дальше.
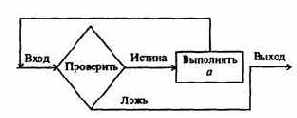
Рис. 1.22. Структура цикла «пока»
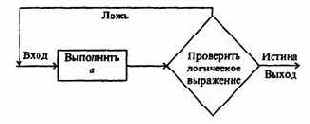
Рис. 1.23. Структура цикла «до»
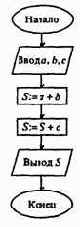
Рис. 1.24. Нахождение суммы трех чисел
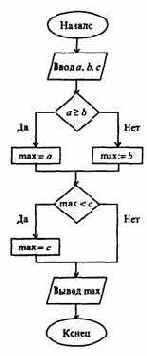
Рис. 1.25. Нахождение наибольшего из трех чисел
Эти структуры можно комбинировать одну с другой - как путем организации их следований, так и путем создания суперпозиций (вложений одной структуры в другую) - сколь угодно разнообразно для выражения логики алгоритма решения любой задачи. Используя описанные структуры, можно полностью исключить использование каких-либо еще операторов условного и безусловного перехода, что является важным признаком структурного программирования. Направление выполнения команд часто изображают сверху вниз. На рис. 1.24 - 1.26 приведены простейшие примеры структурной реализации алгоритмов работы с величинами.
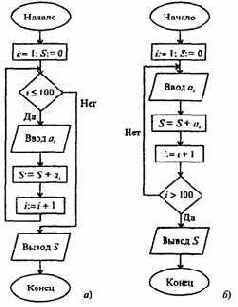
Рис. 1.26. Нахождение суммы 100 чисел
Умение образовывать из базовых структур их суперпозиции в соответствии с условиями конкретной задачи - одно из важнейших в программировании. Допустим, надо ввести в память компьютера 100 чисел и по дороге отсуммировать те из них, которые положительны. Ясно, что ввод - операция циклическая, а внутри этого цикла находится развилка, в которой проверяется знак числа и производится суммирование. Схематически соответствующая суперпозиция изображена на рис. 1.27.
Так как выражение, управляющее циклом, проверяется в самом начале, то в случае, если условие сразу окажется ложным, операторы циклической части «a» могут вообще не выполняться. Операторы циклической части «а» должны изменять переменную (или переменные), влияющие на значение логического выражения, иначе программа «зациклится» - будет выполняться бесконечно.
Рассмотренная циклическая конструкция называется также цикл «пока», или «цикл с предусловием».
Существует и иная конструкция цикла, которая предусматривает проверку условия, по которому, наоборот, выполнение команд циклической части прекращается, после команд циклической части (см. рис. 1.23).
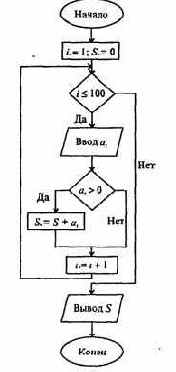
Рис 1.27 Алгоритм типа развилка, вложенная в цикл,
для нахождения суммы положительных чисел из 100 возможных
Схематические изображения нескольких суперпозиций базовых алгоритмических структур представлены ниже на рис. 1.28-1.31.
Еще одним важным компонентом структурного подхода к разработке алгоритмов является модульность. Модуль - это последовательность логически связанных операций, оформленных как отдельная часть программы. Использование модулей имеет следующие преимущества:
1) возможность создания программы несколькими программистами;
2) простота проектирования и последующих модификаций программы;
3) упрощение отладки программы - поиска и устранения в ней ошибок;
4) возможность использования готовых библиотек наиболее употребительных модулей.
Но, пожалуй, самым важным достижением структурного подхода к разработке алгоритмов является нисходящее проектирование программ, основанное на идее уровней абстракции, которые становятся уровнями модулей в разрабатываемой программе. На этапе проектирования строится схема иерархии, изображающая эти уровни. Схема иерархии позволяет программисту сначала сконцентрировать внимание на определении того, что надо сделать в программе, а лишь затем решать, как это надо делать. При нисходящем проектировании исходная, подлежащая решению задача разбивается на ряд подзадач, подчиненных по своему содержанию главной задаче. Такое разбиение называется детализацией или декомпозицией.
 |
 |
|
Рис. 1.28. Алгоритм типа «цикл, вложенный в неполную развилку» |
Рис. 1.29. Алгоритм типа «цикл в цикле» |
 |
 |
|
Рис. 1.30. Алгоритм типа «развилка в развилке» |
Рис. 1.31. Иллюстрация трехкратного вложения одной базовой структуры в другую |
СТРУКТУРЫ ДАННЫХ
Мы уже познакомились с простыми типами real, integer, boolean, byte, char.
В Паскале программист по своему желанию может определить новый тип путем перечисления его элементов - перечисляемый тип, который относится к простым ординальным типам.
Описание перечисляемого типа выполняется в разделе типов по схеме:
type <имя типа> = <список имен>
Примеры:
type operator = (plus,minus,multi, divide);
color = (white,red,blue,yelow,purple,green);
В списке должно быть не более 256 имен.
Поскольку перечисляемый тип относится к ординальным, то к его элементам можно применять функции ord(x), pred(x), succ(x) и операции отношения. Отметим, что данные этого типа не подлежат вводу и выводу с помощью функций ввода/вывода и могут использоваться внутри программы для повышения ее читабельности и понятности.
Для иллюстрации работы с перечисляемыми типами приведем программу 8, переводящую английские названия дней недели на русский язык.
Программа 8
program week;
type days=(mon,tue,wed,thu,fri,sat,sun);
var d:days;
begin
for d:=mon to sun do
case d of
mon: writeln("понедельник");
tue writeln("вторник");
wed writeln("среда");
thu writeln("четверг");
fri writeln("пятница");
sat writein("суббота") ;
sun writeln("воскресенье")
end
end.
Интервальный тип - это подмножество другого уже определенного ординального типа, называемого базовым. Интервал можно задать в разделе типов указанием наименьшего и наибольшего значений, входящих в него и разделяющихся двумя последовательными точками, например:
type days=(mon,tue,wed,thu,fri,sat,sun);
workday s=mon.. fri;
index=1..30;
letter='a'..'z';
Можно задать интервал и в разделе переменных:
vara:1..100;b:-25..25;
Операции и функции - те же, что и для базового типа. Использование интервальных типов в программе позволяет экономить память и проводить во время выполнения программы контроль присваиваний.
Пример: если k - номер месяца в году, то вместо описания
var k:integer;
можно написать
vark:1..12;
Интервальный тип тоже относится к простым ординальным типам.
СОСТАВНЫЕ СТРУКТУРЫ. Данные, с которыми имеет дело ЭВМ, являются абстракциями некоторых реальных или существующих в воображении людей объектов. Мы уже познакомились с некоторыми типами данных: стандартными, перечислимыми, интервалами. Этими типами можно было обойтись при решении простых задач. Однако естественно и часто очень удобно группировать однотипные данные в последовательности - массивы, строки символов, объединять разнотипные данные об одном и том же объекте в виде записей. Значительные удобства представляются пользователю в Паскале при организации однотипных величин в виде множества с соответствующим набором операций: объединения, пересечения и т.д. Наконец, последовательность однотипных величин переменной длины можно представить в Паскале в виде файла данных и хранить на внешних носителях, используя его в разных программах.
Таким образом, подобно составному оператору, содержащему несколько других операторов, составные типы образуются из других типов, при этом существенную роль играет метод образования или структура составного типа.
Часто используемый составной тип - массив. Массив - это последовательность, состоящая из фиксированного числа однотипных элементов. Все элементы массива имеют общее имя (имя массива) и различаются индексами. Индексы можно вычислять, их тип должен быть ординальным. При описании массивов используются служебные слова array и of. В описании массива указывается тип его элементов и типы их индексов.
Схема описания такова:
type <имя типа> = array [<список типов индексов>] оf <тип элементов>
Тип элементов - произвольный, он может быть составным. Число типов индексов называется размерностью массива. После описания типа массива конкретные массивы можно задать в разделе описания переменных.
Например:
type vector = array [1.. 10] of real;
table = array ['A'..'Z',1..5] of integer;
var a,b : vector;
с: table;
Обращение к элементу массива осуществляется с помощью задания имени переменной, за которым следует заключенный в квадратные скобки список индексов элемента.
Например:
а[7]:=3.1; b[k*k+l]:=0; с['М',3]:=-14;
Если массивы имеют одно и то же описание, то во многих версиях Паскаля допустимо их копирование, например b:=а;
Описание массива можно совместить с описанием соответствующих переменных:
var a,b : array [1.. 10] of real;
d : array [byte] of char;
В Турбо-Паскале разрешена инициализация начальных значений составных переменных с помощью, так называемых, типизированных констант. Типизированные константы используются как переменные того же типа. Их применение экономит память, однако они не могут быть использованы для определения других переменных того же типа.
Схема описания констант массива:
const <имя массива>: <тип массива> = (<список значений элементов>)
Тип массива может быть описан ранее:
type digits =
array [1 ..5] of char;
const a : digits =('0';2','4';6';8');
Пример: используя массив, составим программу, которая напечатает на экране 20 чисел Фибоначчи.
Последовательность Фибоначчи определяется равенствами
а[1]=а[2]=1; a[k]=a[k-l]+a[k-2] при к>2.
Использование массива позволяет создать эффективную программу. Для вывода каждого члена последовательности отведем на экране 5 позиций.
Программа 9
program fibon; "''
const n=20;
var a: array[l..n] of integer;
k: integer;
begin
a[l]:=l;a[2]:=l;
for k:=3 to n do a[kl:=a[k-l]+a[k-2];
for k:=l to n do write(a[k]:5);
writeln
end.
Рассмотрим часто встречающуюся задачу упорядочения членов числовой последовательности по какому-либо признаку.
Пример:
упорядочить члены числовой последовательности по возрастанию.
Используем метод упорядочения, носящий имя «пузырек». Будем просматривать пары соседних элементов последовательно справа налево и переставлять элементы в
паре, если они стоят неправильно:
5,3,2,4,1 > 5,3,2,1,4 > 5,3,1,2,4 > 5,1, 3,2,4 > 1,5,3,2,4
В начале просмотра присвоим некоторой логической переменной значение true:
p:=true; если при просмотре пар была хотя бы одна перестановка, изменим значение логической переменной на противоположное: p:=false; это означает, что последовательность еще не была упорядочена и просмотр пар надо повторить. Цикл просмотров заканчивается, если после очередного просмотра выполняется условие: p=true. Последовательность зададим в программе как константмассив из 10 элементов - целых чисел.
Программа 10
program bubble; '
const a:array[l..10] of integer=(19,8,17,6,15,4,13,2,11,0);
var b,i:integer; p :boolean;
begin c1rscr;
for i:=l to 10 do write(a[i]:3);writeln;writeln;
repeat p:=true;
for i:=10 downto 2 do
if a[i]<a[i-l]
then begin
b:=a[il;a[i]:=a[i-l]; ali-1]:=b;p:=false
end
until p=true;
for i:=l to 10 do write(a[i]:3);
writeln
end.
Обработка элементов двумерных массивов (матриц) обычно выполняется с помощью двойного цикла. Один цикл управляет номером строки, другой - номером столбца.
При решении задач на ЭВМ часто возникает необходимость в использовании последовательностей символов. Такую последовательность можно описать как массив символов, однако в Паскале для таких целей имеется специальный тип - string[n] - строка из n символов, где n <= 255. Способы описания переменных - строк - аналогичны описанию массивов.
1. Строковый тип определяется в разделе описания типов, переменные этого типа - в разделе описания переменных:
type word : string[20];
var a,b,c : word;
2. Можно совместить описание строкового типа и соответствующих переменных в разделе описания переменных:
var a,b,c : string[20];
d : string[30];
3. Можно определить строковую переменную и ее начальное значение как констант-строку:
const l:string[l 1]='информатика';
Символы, составляющие строку, занумерованы слева направо; к ним можно обращаться с помощью индексов, как к элементам одномерного массива.
Для переменных одного строкового типа определен лексикографический порядок, являющийся следствием упорядоченности символьного типа:
'fife' < 'tree' (так как 'f' < 't'); '4' > '237' (так как '4' > '2').
Кроме логических операций <, >, =, для величин строкового типа определена некоммутативная операция соединения, обозначаемая знаком плюс:
а:='кол'+'о'+'кол'; (в результате а='колокол').
Для строковых величин определены следующие четыре стандартные функции.
1. Функция соединения - concat(sl,s2,...,sk). Значение функции - результат соединения строк sl ,s2,...sk, если он содержит не более 255 символов.
2. Функция выделения - copy(s,i,k). Из строки s выделяется k символов, начиная с i-того символа:
а:=сору('крокодил',4,3); (в результате а='код*).
3. Функция определения длины строки - length(s). Вычисляется количество символов, составляющих текущее значение строки s:
b:=length('каникулы'); (b=8).
4. Функция определения позиции - pos(s,t). Вычисляется номер позиции, начиная с которого строка s входит первый раз в строку t; результат равен 0, если строка s не входит в t:
с:=роs('ом','компьютер'); (с=2).
В Паскале определены также четыре стандартные процедуры для обработки строковых величин:
1. Процедура удаления delete(s,i,k). Из строки s удаляется k символов, начиная с i-того символа.
s:='таракан'; delete(s,5,2); (в результате S='таран').
2. Процедура вставки - insert(s,t,i). Строка s вставляется в строку t, начиная с позиции i:
t:='таран'; insert ('ka',t,5); (t='таракан').
3. Процедура преобразования числа в строку символов - str(k,s). Строка s получается «навешиванием» апострофов на число k:
str(564,s); (s='564').
4. Процедура преобразования строки из цифр в число - val(s,k,i). Число i=0, если в строке s нет символов, отличных от цифр, в противном случае i=позиции первого символа, отличного от цифры:
val('780',k,i); (k=780; i=0).
Рассмотрим несколько программ, в которых используются строковые величины.
1. Составить программу, определяющую количество гласных в русском тексте, содержащем не более 100 символов.
Здесь удобно определить констант-строку, состоящую из всех 18 строчных и заглавных русских букв, и в цикле проверить, будет ли очередной символ заданного текста элементом констант-строки.
Программа 11
program vowel;
const с:зtring[18]='аеиоуыэюяАЕИОУЫЭЮЯ' ;
var a :string[100]; k,n:integer;
begin
writeln('введите текст'); readln(a);n:=0;
for k:=l to length(a) do
if pos(a[k],c)>0 then n:=n+l;
writeln('кол. гласных=',n) end.
2. Заменить в арифметическом выражении функцию sqr на ехр. Замена выражения sqr на ехр достигается последовательным применением процедур delete и insert:
Программа 12
program stroka;
var a,b:string[40]; k:integer;
begin
writeln('введите строку <= 40 символов');
readin(a);b:=a;
repeat k:=pos('sqr',b);
if k>0 then
begin
delete(b,k,3);insert('ехр',b,k) ;
end
until k=0;
writein('старая строка=',a); writein('новая строка"',b);
end.
3. Ввести и упорядочить по алфавиту 10 латинских слов. В программе определим массив из 10 элементов-строк и упорядочим его элементы методом пузырька.
Программа 13
program order;
const s=10;
type word=string(20] ;
var i, j, k : 1. . s;
b:word; p:boolean; list :array[l..s] of word;
begin
clrscr;writeln<'введите список слов');
for i:=l to s do readln(list[i]);
repeat p:=true;
for i:=s downto 2 do
if list[i]<list[i-l] then
begin
b:list[i);list[i]:=list[i-l]; list[i-l]:=b;p:=false end
until p=true;
writein('упорядоченный список слов:');
for i:=l to s do writeln(list[i])
end.
Множество в Паскале имеет такой же смысл, как и в алгебре - это неупорядоченная совокупность отличных друг от друга однотипных элементов. Число элементов множества не должно превышать 255. В качестве типа элементов может быть любой скалярный тип, кроме типа integer и его интервалов, содержащих числа > 255.
Тип элементов множества называется базовым. При описании множественного типа используются служебные слова set и of. Задание конкретного множества определяется правилом (конструктором) - списком элементов или интервалов, заключенным в квадратные скобки. Пустое множество обозначается двумя символами [].
Множественный тип можно определить в разделе описания типов по схеме:
type <имя> = set of <тип элементов>
Например:
type t=set of byte;
var a:t;
Можно совместить описание множественного типа и соответствующих переменных:
var code: set of0..7;
digits: set of'0'..'9';
Можно описать переменную множественного типа и задать ее первоначальное значение в разделе описания констант, как константмножество. Тип множества можно описать ранее, например,
type up=setof'A'..'Z';
low=set of'a'.. "z";
const upcase : up=['A'. . 'Z'];
vocals :low=['a', 'e', 'i', 'o', "u", 'y'];
delimiterset of char=[ '..' /',':'..' ? '];
Для данных множественного типа определены операции объединения, пересечения и дополнения множеств, обозначаемые в Паскале соответственно знаками +, * и -, а также отношения равенства множеств (А=В), неравенства (А<>В), включения (А<=В,А>=В).
Логическая операция принадлежности х in А принимает значение true, если элемент х принадлежит множеству А и false в противном случае. Так как к элементам множества прямого доступа нет, то операция in часто используется для этой цели.
Заметим, что операции отношения на множествах выполняются быстрее, чем соответствующие операции на числах, поэтому их выгодно применять в программах.
Пример: составить программу, анализирующую латинский текст и печатающую в алфавитном порядке все найденные в нем буквы, а затем все ненайденные.
Пусть alfa - множество всех букв латинского алфавита. Будем вводить заданный текст с клавиатуры символ за символом, одновременно формируя множество Е -множество латинских букв текста. В конце текста введем символ *. Затем с помощью операции in будем проверять, какие буквы алфавита имеются во множестве Е.
Множество N - ненайденных букв в тексте - определяется оператором: N := alfa - Е .
Программа 14
program search;
const alfa:set of char=['a' . .'z'];
var c:char;E,N:set of char;
begin
cirscr; E:=[]; writeln('введите текст, конец ввода -*'); read(c);
while c<> '*' do
begin
if с in alfa then E:=E+[c]; read(c)
end;
writeln;
if E=alfa then writeln('найдены все латинские буквы')
else begin
N:=alfa-E;
writeln('найдены:');
for c:='a' to 'z' do if с in E then write(c);
writeln; writeln('не найдены:');
for c:='a' to 'z' do if с in N then write(c);
writeln
end
end.
Переменные множественного типа удобно применять в задачах, где порядок данных не имеет значения, например при моделировании случайных событий.
Пример: составить программу «спортлото 5 из 36», которая позволяет человеку ввести с клавиатуры пять натуральных чисел из интервала 1..36, затем генерирует случайным образом пять различных чисел из того же интервала и объявляет величину выигрыша по правилу: если угаданы человеком 0, 1 или 2 числа, объявляется проигрыш; если угаданы 3 числа, объявляется выигрыш 3 рубля; если угаданы 4 числа, объявляется выигрыш 100 рублей; если угаданы 5 чисел, объявляется выигрыш 1000 рублей.
В программе используются обозначения: mn — множество натуральных чисел из интервала 1 . . 36, а - множество чисел, задуманных человеком, х - множество чисел, . генерируемых компьютером, z=a*x - пересечение множеств а и х; i, k, s - переменные, значения которых принадлежат интервалу 1..36. Случайное число из этого интервала генерируется оператором: s:=random(35)+l. Программа сначала выводит на экран сообщение о выигрышных номерах, затем определяет величину выигрыша.
Программа 15
program lottery;
type mn = set of 1 . . 36;
var x,a, z: nm; i, k, s: 0 . . 36;
begin
writeln; a:=[];
for i:=l to 5 do
begin write('введите ',i,' -тое число '); readin(k);a:=a+[k] end;
randomize;
k:=0; x:=[];
while k<5 do
begin
s:random (35) +1;
if not(s in x) then begin k:=k+l; x:=x+[s]
end
end; writeln;
writeln(' выигрыш выпал на следующие номера : ');
for i:=l to 36 do if (i in x) then write(i,' ');
writeln; z:=a*x; k:=0;
for i:=l to 36 do if (i in z) then begin writeln('угадано: ',i); k:=k+l
end;
case k of
0, 1, 2 : writeln('вы проиграли ');
3 : writeln('получите 3 руб') ;
4 : writeln('получите 100 руб');
5 : writein('получите 1000 руб')
end
end.
Записи (комбинированный тип) - одна из наиболее гибких и удобных структур данных, применяющихся при описании сложных объектов, которые характеризуются различными свойствами, а также при создании различных информационных систем. Запись - это последовательность, состоящая из фиксированного числа величин разных типов, называемых полями или компонентами записи. Так же, как и массив, запись содержит ряд отдельных компонент, но компонентами записи могут быть данные различных типов. Например, адресные данные (индекс, город, улица, номер дома, квартиры) можно представить как запись (record):
type address = record
index : string[6];
city: string[20];
street : string[20];
haus.ilat: integer
end;
Из примера видно, что тип «запись» описывается по схеме
type имя типа записи = record
имя поля 1 : тип;
имя поля 2 : тип;
имя поля N: тип
end;
Как и при описании массивов, можно совместить описание типа записи и соответствующих переменных. Например, данные о двух студентах можно описать так:
fio :string[20];
fas :string[10]
grup :string[8]
end
Переменную типа «запись» и ее первоначальное значение можно определить как констант-запись в разделе констант по схеме
const
<имя>: <имя типа> = <константное значение>
Константное значение - это список имен полей и соответствующих значений, заключенный в круглые скобки. Элементы списка разделяются знаком «точка с запятой». Например, запись о начале координат можно определить так:
type point = record
х, у, z: integer
end;
const o: point = (x:0; y:0; z:0);
С компонентами записи можно обращаться как с переменными соответствующего типа. Обращение к компонентам записи осуществляется с помощью указания имени поля через точку. Пусть, например, переменная х имеет тип address, т.е. в программе имеется описание var x: address. Тогда допустимы следующие присваивания:
x.haus := 52; х.street:='пр.Мира'; x.city:= 'Красноярск';
x.flat:= 135; x.index :='б60049'
Проиллюстрируем работу с записями на задаче, в которой требуется найти сумму и произведение двух комплексных чисел:
zl=al+i*blиz2=a2+i*b2.
Программа 16
program cornpl;
type compi = record
re : real;
im : real
end;
var zl,z2,s,p : compl;
begin
writeln('компл.число a+i*b вводите
двумя числами
а и
Ь: 'it-write('введи 1 число: '); readln(zl.re,zl.im);
write('введи 2 число: '); readin(z2.re,z2.im);
s.re := zl.re + z2.re;
s.im := zl.re + z2.im;
p.re := zl.re * z2.re - zl.im * z2.im;
p.im := zl.re * z2.im + z2.re * zl.im;
writeln('s=',s.re:4:2,' + i *',s.im:4:2);
write('p=',p.re:4:2,' + i *',p.im:4:2)
end.
Громоздкость обозначений в программе компенсируется большей наглядностью алгоритма за счет структуризации данных. Во многих случаях, если требуется производить операции с полями фиксированной записи, можно для сокращения обозначений использовать оператор присоединения with. Его структура такова:
with <имя записи> do <оператор>;
В этом случае в операторе, написанном после служебного слова do, имена полей указанной записи описываются без имени записи и точки. Например, печать суммы s в предыдущем примере можно организовать с использованием оператора with так:
with s do writeln('s=',re:4:2,'+i*',im:4:2);
В операторах присваивания разрешается использовать не только имена полей, но и имена записей.
Тип поля может быть записью.
Например:
man = record
fio:record
fam, im, otch : string[10];
end;
data : record
day: 1..31;
mes:1..12;
god:integer
end;
pol: char;
telef: record
dom,rab : string[10];
end;
end;
В Паскале разрешается использовать тип «запись» при описании других составных типов данных, например, можно построить массив записей.
Рассмотрим пример эффективного использования записей в программе начисления стипендии студентам по шаблону:
N ФИО Эк1 Эк2 ЭкЗ Балл Сумма Проф Итого
1 Васнецов Н.В. 4 4 3 11 50.00 0.25 49.75
Предположим, что вводится список группы с соответствующими оценками за экзамены. Графа «Балл» вычисляет суммарную оценку за семестр. Графа «Сумма» определяет размер стипендии по упрощенному правилу: если нет двоек и балл равен 15, то стипендия 75 руб.; при условии, что 12 < «Балл» < 15 стипендия 62 руб 50 коп., а если 9 < «Балл» < 12 , то - 50 руб. (в других случаях сумма равна нулю). В графе «Проф» указывается профсоюзный взнос в размере 0,5% от стипендии, а графа «Итого» определяет сумму денег к выдаче.
В программе перед распечаткой итоговой ведомости можно предусмотреть упорядочение записей по убыванию в графе «Балл».
Программа 17
program spisok;
type stud = record
fio :string[20];
ex1, ex2, ex3 : 2 . . 5;
bal :6 . . 15;
sum :real;
nalog :real;
itog :real;
end;
var x : array[1..30] of stud;
i,k,m,n :integer;
у : 6..15;
z : stud;
begin write('введи
число студентов: '); readln(n);
for i:= 1 to n do with x[i] do
begin write('введи
ФИО ',i,'-ro студента: ');
readln(fio); write('Bведи его
три оценки: ');
readin(exl,ex2,ex3);
end;
for i:= 1 to n do with x[i] do
begin bal:=exl+ex2+ex3;
if (exl=2) or (ex2=2) or (ex3=2)
then sum:=0
else if bal=15 then sum:=75
else if bal>12 then sum:=62.5
else if bal>9 then sum:=50
else sum:=0;
nalog:=sum*0.005; itog:=sum-nalog;
end;
for k:= 1 to n-1 do
begin y:=x[k].bal; m:=k;
for i:=k+l to n do if y<x[i].bal then
begin y:=x[i].bal; m:=i
end; z:=x[k]; x(k]:=x[m]; x(m]:=z;
end;
writeln; writeln ('СТИПЕНДИАЛЬНАЯ ВЕДОМОСТЬ ');
for i:=l to 64 do write('-'); writeln;
write ('N | ФИО
| эк1 | эк2 | эк3 | балл | сумма | проф | итого |') ;
for i:=l to 64 do write('-'); writeln;
for i:=l to n do with x[i] do
begin write(i:3,fio:20,exi:4, ex2:4,ex3:4);
writeln(bal:5,sum:9:2,nalog:8:2,- itog:7:2);
end
end.
Контрольные вопросы и задания
1. Как определяется перечислимый тип данных?
2. Для чего может понадобиться интервальный тип данных?
3. Как вводятся и используются в программах массивы?
4. Какие действия возможны над величинами строкового типа?
5. Какие операции допустимы над множествами?
6. В чем принципиальные различия между одномерными массивами и записями?
7. В усеченном конусе длина диагонали осевого сечения равна d, образующая составляет с плоскостью основания угол х и равна а. Вычислите площадь боковой поверхности конуса.
8. Вычислите объем призмы, боковые грани которой квадраты, а основанием служит равносторонний треугольник, вписанный в круг радиуса г.
9. Числа а и b выражают длины катетов одного прямоугольного треугольника, числа с и d - другого. Определите, являются ли треугольники подобными.
10. Напечатайте числа а, b, с в порядке возрастания.
11. Определите все пары двузначных чисел, обладающих свойством: (20+25^2 = = 2025.
12. Вычислите в числовом массиве а1,а2,...,аn суммы положительных и отрицательных элементов.
13. Вычислите скалярное произведение двух десятимерных векторов Х и Y.
14. Упорядочите массив х1,х2,...,хn по неубыванию, используя метод сортировки вставками: пусть первые k элементов уже упорядочены по неубыванию; берется (K+1)-й элемент и размещается среди первых k элементов так, чтобы упорядоченными оказались уже (k+1) первых элементов.
15. Составьте программу решения треугольной системы уравнений порядка n.
16. Замените в заданном арифметическом выражении все вхождения sin на cos и sqrt на abs.
17. Для заданного текста определите длину содержащейся в нем максимальной последовательности цифр 0, 1,2,..., 9.
18. Дан текст из латинских букв и знаков препинания. Составьте программу частотного анализа букв этого текста, т.е. напечатайте каждую букву с указанием количества ее вхождений и процента вхождений.
19. Найдите и напечатайте в порядке убывания все простые числа из диапазона [2..201].
20. Опишите тип «запись» для следующих данных:
а) адрес(город, улица, дом, квартира);
б) дата(число,месяц.год);
в) студент(фио,факультет,курс,группа).
21. Заданы N точек на плоскости. Найдите точку, ближайшую к началу координат. Используйте тип «запись».
СВЯЗИ МЕЖДУ ОБЪЕКТАМИ
В реальном мире между предметами существуют различные отношения. Если предметы моделируются как объекты, то отношения, которые систематически возникают между различными видами объектов, отражаются в информационных моделях как связи. Каждая
связь задается в модели определенным именем. Связь в графической форме представляется как линия между связанными объектами и обозначается идентификатором связи.
Существует три вида связи: один-к-одному (рис. 1.39), один-ко-многнм (рис. 1.40) и многие-ко-многим (рис. 1.41).
Связь один-к-одному существует, когда один экземпляр одного объекта связан с единственным экземпляром другого. Связь один-к-одному обозначается стрелками <и>.

Рис. 1.39. Пример связи «одии-к-одному»
Связь один-ко-многим существует, когда один экземпляр первого объекта связан с одним (или более) экземпляром второго объекта, но каждый экземпляр второго объекта связан только с одним экземпляром первого. Множественность связи изображается двойной стрелкой >>.

Рис. 1.40. Пример связи «один-ко-многим»
Связь многие-ко-многим существует, когда один экземпляр первого объекта связан с одним или большим количеством экземпляров второго и каждый экземпляр второго связан с одним или многими экземплярами первого. Этот тип связи изображается двусторонней стрелкой -

Рис. 1.41. Пример связи «многие-ко-многим»
Помимо множественности, связи могут подразделяться на безусловные и условные. В безусловной связи для участия в ней требуется каждый экземпляр объекта. В условной связи принимают участие не все экземпляры объекта. Связь может быть условной как с одной, так и с обеих сторон.
Все связи в информационной модели требуют описания, которое, как минимум, включает:
• идентификатор связи;
• формулировку сущности связи;
• вид связи (ее множественность и условность);
• способ описания связи с помощью вспомогательных атрибутов объектов.
Дальнейшее развитие представлений информационного моделирования связано с развитием понятия связи, структур, ими образуемых, и задач, которые могут быть решены на этих структурах.
Нам уже известна простая последовательная структура экземпляров - очередь, см. рис. 1.34. Возможными обобщениями информационных моделей являются циклическая структура, таблица (см. табл. 1.10), стек (см. рис. 1.35).
Очень важную роль играет древовидная информационная модель, являющаяся одной из самых распространенных типов классификационных структур. Эта модель строится на основе связи, отражающей отношение части к целому: «А есть часть М» или «М управляет А». Очевидно, древовидная связь является безусловной связью типа один-ко-многим и графически изображена на рис. 1.42, в. На этом же рисунке для сравнения приведены схемы информационных моделей типа «очередь» (а) и «цикл» (б).
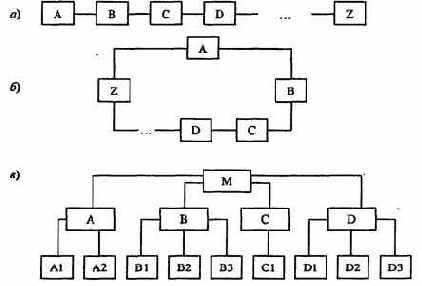
Рис. 1.42. Информационные модели типа «очередь» (а), «цикл» (б), «дерево» (в)
Таким образом, типы данных в программировании, обсуждавшиеся в предыдущем параграфе, тесно связаны с определенными информационными моделями данных.
Еще более общей информационной моделью является, так называемая, графовая структура, рис. 1.43. Графовые структуры являются основой решения огромного количества задач информационного моделирования.
Многие прикладные задачи информационного моделирования были поставлены и изучены достаточно давно, в 50-60-х годах, в связи с активно развивавшимися тогда исследованиями и разработками по научным основам управления в системах различной природы и в связи с попытками смоделировать с помощью компьютеров психическую деятельность человека при решении творческих интеллектуальных задач. Научное знание и модели, которые были получены в ходе решения этих задач, объединены в науке под названием «Кибернетика», в рамках которой существует раздел «Исследования по искусственному интеллекту».
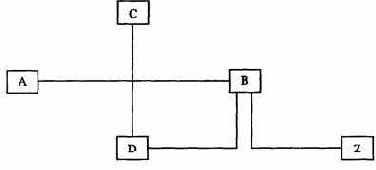
Рис. 1.43. Информационная модель типа «граф»
СВОБОДНОЕ ПАДЕНИЕ ТЕЛА С УЧЕТОМ СОПРОТИВЛЕНИЯ СРЕДЫ
При реальных физических движениях тел в газовой или жидкостной среде трение накладывает огромный отпечаток на характер движения. Каждый понимает, что предмет, сброшенный с большой высоты (например, парашютист, прыгнувший с самолета), вовсе не движется равноускоренно, так как по мере набора скорости возрастает сила сопротивления среды. Даже эту. относительно несложную, задачу нельзя решить средствами «школьной» физики; таких задач, представляющих практический интерес, очень много. Прежде чем приступать к обсуждению соответствующих моделей, вспомним, что известно о силе сопротивления.
Закономерности, обсуждаемые ниже, носят эмпирический характер и отнюдь не имеют столь строгой и четкой формулировки, как второй закон Ньютона. О силе сопротивления среды движущемуся телу известно, что она, вообще говоря, растет с ростом скорости (хотя это утверждение не является абсолютным). При относительно малых скоростях величина силы сопротивления пропорциональна скорости и имеет место соотношение Fcoпp = k1v, где k1 определяется свойствами среды и формой тела. Например, для шарика k1 = 6??r - это формула Стокса, где ?
-динамическая вязкость среды, r -
радиус шарика. Так, для воздуха при t
= 20°С и давлении 1 атм.? = 0,0182 Н•с•м-2, для воды 1,002 Н•с•м-2, для глицерина 1480 Н•с•м-2.
Оценим, при какой скорости для падающего вертикально шара сила сопротивления сравняется с силой тяжести (и движение станет равномерным).
Имеем
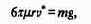
или
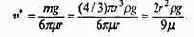
Пусть r
= 0,1 м, ? = 0,8•103
кг/м3 (дерево). При падении в воздухе v* ? 960 м/с, в воде v*? 17 м/с, в глицерине v* ? 0,012 м/с.
На самом деле первые два результата совершенно не соответствуют действительности. Дело в том, что уже при гораздо меньших скоростях сила сопротивления становится пропорциональной квадрату скорости: Fcoпp
= k2v2. Разумеется, линейная по скорости часть силы сопротивления формально также сохранится, но если k2v2>> k1v, то вкладом k1v можно пренебречь (это конкретный пример ранжирования факторов).
О величине k2 известно следующее: она пропорциональна площади сечения тела S,
поперечного по отношению к потоку, и плотности среды ?среды и зависит от формы тела. Обычно представляют k2
= 0,5сS?срeды, где с - коэффициент лобового сопротивления - безразмерен. Некоторые значения с (для не очень больших скоростей) приведены на рис. 7.6.
При достижении достаточно большой скорости, когда образующиеся за обтекаемым телом вихри газа или жидкости начинают интенсивно отрываться от тела, значение с в несколько раз уменьшается; для шара оно становится приблизительно равным 0,1. Подробности можно найти в специальной литературе.
Вернемся к указанной выше оценке, исходя из квадратичной зависимости силы сопротивления от скорости.
Имеем
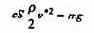
или
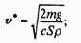
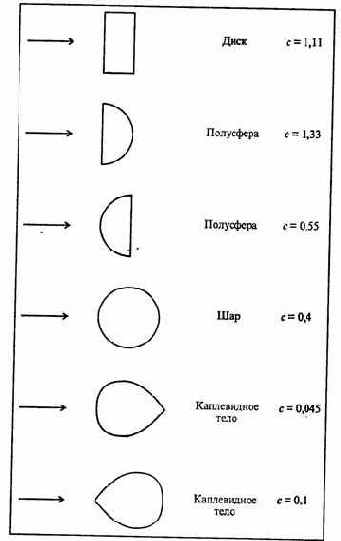
Рис. 7.6. Значения коэффициента лобового сопротивления для некоторых тел, поперечное сечение которых имеет указанную на рисунке форму (см. книгу П.А.Стрелкова)
Для шарика
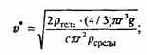
Примем r = 0,1 м, ? = 0,8•103 кг/м3 (дерево). Тогда для движения в воздухе (?возд= 1,29 кг/м3) получаем v*
? 18 м/с, в воде (?воды ? 1•103 кг/м3) v* ? 0,65 м/с, в глицерине (?глицерина = 1,26•103
кг/м3) v* ? 0,58 м/с.
Сравнивая с приведенными выше оценками линейной части силы сопротивления, видим, что для движения в воздухе и в воде ее квадратичная часть сделает движение равномерным задолго до того, как это могла бы сделать линейная часть, а для очень вязкого глицерина справедливо обратное утверждение. Рассмотрим свободное падение с учетом сопротивления среды. Математическая модель движения - уравнение второго закона Ньютона с учетом двух сил, действующих на тело; силы тяжести и силы сопротивления среды:
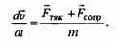
Движение является одномерным; проецируя векторное уравнение на ось, направленную вертикально вниз, получаем
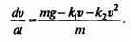
Вопрос, который мы будем обсуждать на первом этапе, таков: каков характер изменения скорости со временем, если все параметры, входящие в уравнение (7.7), заданы? При такой постановке модель носит сугубо дескриптивный характер.
Из соображений здравого смысла ясно, что при наличии сопротивления, растущего со скоростью, в какой-то момент сила сопротивления сравняется с силой тяжести, после чего скорость больше возрастать не будет. Начиная с этого момента, dv/dt = 0, и соответствующую установившуюся скорость

= 0 , решая не дифференциальное, а квадратное уравнение. Имеем
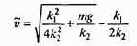
(второй - отрицательный - корень, естественно, отбрасываем). Итак, характер движения качественно таков: скорость при падении возрастает от v0
до

как и по какому закону - это можно узнать, лишь решив дифференциальное уравнение (7.7).
Однако, даже в столь простой задаче мы пришли к дифференциальному уравнению, которое не относится ни к одному из стандартных типов, выделяемых в учебниках по дифференциальным уравнениям, допускающих очевидным образом аналитическое решение. II хотя это не доказывает невозможность его аналитического решения путем хитроумных подстановок, но они не очевидны (один из лучших помощников в их поиске - справочник Камке). Допустим, однако, что нам удастся найти такое решение, выраженное через суперпозицию нескольких алгебраических и трансцендентных функций - а как найти закон изменения во времени перемещения? - Формальный ответ прост:
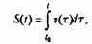
но шансы на реализацию этой квадратуры уже совсем невелики. Дело в том, что класс привычных нам элементарных функций очень узок, и совершенно стандартна ситуация, когда интеграл от суперпозиции элементарных функций не может быть выражен через элементарные функции в принципе. Математики давно расширили множество функций, с которыми можно работать почти так же просто, как с элементарными (т.е. находить значения, различные асимптотики, строить графики, дифференцировать, интегрировать). Тем, кто знаком с функциями Бесселя, Лежандра, интегральными функциями и еще двумя десятками других, так называемых, специальных функций, легче находить аналитические решения задач моделирования, опирающихся на аппарат дифференциальных уравнений.
Однако даже получение результата в виде формулы не снимает проблемы представления его в виде, максимально доступном для понимания, чувственного восприятия, ибо мало кто может, имея формулу, в которой сопряжены логарифмы, степени, корни, синусы и тем более специальные функции, детально представить себе описываемый ею процесс -а именно это есть цель моделирования.
В достижении этой цели компьютер - незаменимый помощник. Независимо от того, какой будет процедура получения решения - аналитической или численной, -задумаемся об удобных способах представления результатов. Разумеется, колонки чисел, которых проще всего добиться от компьютера (что при табулировании формулы, найденной аналитически, что в результате численного решения дифференциального уравнения), необходимы; следует лишь решить, в какой форме и размерах они удобны для восприятия. Слишком много чисел в колонке быть не должно, их трудно будет воспринимать, поэтому шаг, с которым заполняется таблица, вообще говоря, гораздо больше шага, с которым решается дифференциальное уравнение в случае численного интегрирования, т.е. далеко не все значения v и S,
найденные компьютером, следует записывать в результирующую таблицу (табл. 7.2).
Таблица 7.2
Зависимость перемещения и скорости падения «безпарашютиста» от времени (от 0 до 15 с)
|
t(c) |
s(m) |
v (м/с) |
t(с) |
S(м) |
v (м/с) |
|
0 |
0 |
0 |
8 |
200,1 |
35,6 |
|
1 |
4,8 |
9,6 |
9 |
235,9 |
36,0 |
|
2 |
18,7 |
17,9 |
10 |
272,1 |
36,3 |
|
3 |
40,1 |
24,4 |
11 |
308,5 |
36,4 |
|
4 |
66,9 |
28,9 |
12 |
345,0 |
36,5 |
|
5 |
97,4 |
31,9 |
13 |
381,5 |
36,6 |
|
6 |
130,3 |
33,8 |
14 |
418.1 |
36,6 |
|
7 |
164,7 |
35,0 |
15 |
454,7 |
36,6 |
по ним хорошо видно, как меняются со временем скорость и перемещение, т.е. приходит качественное понимание процесса.
Еще один элемент наглядности может внести изображение падающего тела через равные промежутки времени.
Ясно, что при стабилизации скорости расстояния между изображениями станут равными. Можно прибегнуть и к цветовой раскраске - приему научной графики, описанному выше.
Наконец, можно запрограммировать звуковые сигналы, которые подаются через каждый фиксированный отрезок пути, пройденный телом - скажем, через каждый метр или каждые 100 метров - смотря по конкретным обстоятельствам. Надо выбрать интервал так, чтобы вначале сигналы были редкими, а потом, с ростом скорости, сигнал слышался все чаще, пока промежутки не сравняются. Таким образом, восприятию помогают элементы мультимедиа. Поле для фантазии здесь велико.
Приведем конкретный пример решения задачи о свободно падающем теле. Герой знаменитого фильма «Небесный тихоход» майор Булочкин, упав с высоты 6000 м в реку без парашюта, не только остался жив, но даже смог снова летать. Попробуем понять, возможно ли такое на самом деле или же подобное случается только в кино. Учитывая сказанное выше о математическом характере задачи, выберем путь численного моделирования. Итак, математическая модель выражается системой дифференциальных уравнений
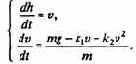
Разумеется, это не только абстрактное выражение обсуждаемой физической ситуации, но и сильно идеализированное, т.е. ранжирование факторов перед построением математической модели произведено. Обсудим, нельзя ли произвести дополнительное ранжирование уже в рамках самой математической модели с учетом конкретно решаемой задачи, а именно - будет ли влиять на полет парашютиста линейная часть силы сопротивления и стоит ли ее учитывать при моделировании.
Так как постановка задачи должна быть конкретной, мы примем соглашение, каким образом падает человек. Он - опытный летчик и наверняка совершал раньше прыжки с парашютом, поэтому, стремясь уменьшить скорость, он падает не «солдатиком», а лицом вниз, «лежа», раскинув руки в стороны. Рост человека возьмем средний - 1,7 м, а полуобхват грудной клетки выберем в качестве характерного расстояния - это приблизительно 0,4 м.
Для оценки порядка величины линейной составляющей силы сопротивления воспользуемся формулой Стокса. Для оценки квадратичной составляющей силы сопротивления мы должны определиться со значениями коэффициента лобового сопротивления и площадью тела. Выберем в качестве коэффициента число с = 1,2 как среднее между коэффициентами для диска и для полусферы (выбор для качественной оценки правдоподобен). Оценим площадь: S =
1,7•0,4=0,7 (м2).
Выясним, при какой скорости сравняются линейная и квадратичная составляющие силы сопротивления. Обозначим эту скорость v**. Тогда
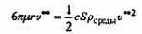
или

Ясно, что практически с самого начала скорость падения майора Булочкина гораздо больше, и поэтому линейной составляющей силы сопротивления можно пренебречь, оставив лишь квадратичную составляющую.
После оценки всех параметров можно приступить к численному решению задачи. При этом следует воспользоваться любым из известных численных методов интегрирования систем обыкновенных дифференциальных уравнений: методом Эйлера, одним из методов группы Рунге - Кутта, одним из многочисленных неявных методов. Разумеется, у них разная устойчивость, эффективность и т.д. - эти сугубо математические проблемы здесь не обсуждаются. Программа, реализующая метод Рунге - Кутта четвертого порядка, может быть взята из примера, приведенного в следующем параграфе или из какого-нибудь стандартного пакета математических программ.
Отметим, что существует немало программ, моделирующих простые физические процессы типа рассматриваемого. У них реализован, в той или иной мере профессионально, диалоговый интерфейс, позволяющий вводить параметры, получать на экране таблицы, графики, движущиеся изображения. Однако в них, как правило, остаются скрытыми физические законы, определяющие процесс, ограничения модели, возможности ее усовершенствования. Такие программы полезны скорее как сугубо иллюстративные.
Вычисления производились до тех пор, пока «безпарашютист» не опустился на воду. Примерно через 15 с после начала полета скорость стала постоянной и оставалась такой до приземления (рис. 7.7).
Отметим, что в рассматриваемой ситуации сопротивление воздуха радикально меняет характер движения; при отказе от его учета график скорости, изображенный на рисунке, заменился бы касательной к нему в начале координат.
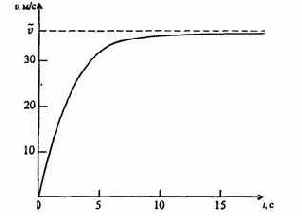
Рис. 7.7. График зависимости скорости падения «безпарашютиста» от времени
В некоторых случаях для ускорения процесса работы над какой-либо задачей целесообразно вместо составления программы воспользоваться готовой прикладной программой (например, табличным процессором). Покажем это на примере рассматриваемой задачи. В табл. 7.3 представлен небольшой фрагмент из табличного процессора Excel. Решение находится с помощью, так называемого, исправленного метода Эйлера - одного из возможных вариантов метода Рунге - Кутта второго порядка.
Кроме того, в ячейках D2, D4, D6 в таблице будем хранить соответственно значения шага вычислений, массы «безпарашютиста», величины mg. Это связано с тем, что все константы также удобно хранить в отдельных ячейках, чтобы в случае их изменения не пришлось переписывать расчетные формулы. Достаточно записать
Таблица 7.3
Фрагмент таблицы, где представлено решение задачи о «безпарашютнсте»
|
А |
В |
|
|
1 |
t |
v |
|
2 |
||
|
3 |
0 |
0 |
|
4 |
=СУММ(АЗ; D2) |
=B3+D2/2* ( (D6-D8*B3^2) /D4+(D6-D8*(B3+D2*(D6-D8*B3^2)/D4)^2)/D4) |
|
5 |
=СУММ(А4; D2) |
=B4+D2/2* ( (D6-D8*B4^2) /D4+(D6-D8* (B4+D2* (D6- D8*B4^2)/D4)^2)/D4) |
|
6 |
=СУММ(А5; D2) |
=B5+D2/2*( (D6-D8*B5^2)/D4+(D6-D8*(B5+D2*(D6-D8*B5^2)/D4)^2)/D4) |
|
7 |
=СУМM(А6; D2) |
=B6+D2/2* ( (D6-D8*B6^2) /D4+ (D6-D8* (B6+D2* (D6-D8*B6^2)/D4)^2)/D4) |
|
8 |
=СУММ(А7; D2) |
=B7+D2/2*((D6-D8*B7^2)/D4+(D6-D8*(B7+D2*(D6-D8*B7^2)/D4)^2)/D4) |
Таблица 7.4
Результаты вычислений, выполненных в табличном процессоре
|
А |
В |
С |
D |
|
|
1 |
t |
v |
H |
|
|
2 |
0,001 |
|||
|
3 |
0 |
0 |
т |
|
|
4 |
0,001 |
0,00981 |
80 |
|
|
5 |
0,002 |
0,01962 |
m*g |
|
|
6 |
0,003 |
0,02943 |
784,8 |
|
|
7 |
0,004 |
0,03924 |
k2 |
|
|
8 |
0,005 |
0,04905 |
0,55083 |
|
|
9 |
0,006 |
0,05886 |
Следует заметить, что для хранения результатов расчетов в данном случае требуется очень много ячеек таблицы, и хотя современные табличные процессоры позволяют хранить большой объем информации, в случае нехватки памяти рекомендуется увеличить шаг, с которым проводятся вычисления (при этом пожертвуем точностью вычислений). Табличный процессор позволяет представлять результаты расчетов и в графической форме. Можно при работе над задачей получить результаты двумя способами: с помощью табличного процессора и составлением собственной программы - для того. чтобы затем сравнить эти результаты и временные затраты каждого из способов. Но, несмотря на успешное применение табличного процессора при решении простейшей учебной задачи, следует признать, что для решения более громоздких в вычислительном плане задач предпочтительнее программировать самим. А теперь ответим на вопрос, поставленный в задаче. Известен такой факт: один из американских каскадеров совершил прыжок в воду с высоты 75 м (Бруклинский мост), и скорость приземления была 33 м/с. Сравнение
этой величины с получившейся у нас конечной скоростью 37,76 м/с позволяет считать описанный в кинофильме эпизод вполне возможным. Обсуждаемой модели можно придать черты оптимизационной, поставив задачу так: парашютист прыгает с некоторой высоты и летит, не открывая парашюта; на какой высоте (или через какое время) ему следует открыть парашют, чтобы иметь к моменту приземления безопасную скорость? Или по-другому: как связана высота прыжка с площадью поперечного сечения парашюта (входящей в k2), чтобы скорость приземления была безопасной? Выполнение таких исследований многократно более трудоемко, нежели просто изучение одного прыжка при заказанных условиях.
СВОЙСТВА АЛГОРИТМОВ
Алгоритм должен быть составлен таким образом, чтобы исполнитель, в расчете на которого он создан, мог однозначно и точно следовать командам алгоритма и эффективно получать определенный результат. Это накладывает на записи алгоритмов ряд обязательных требований, суть которых вытекает, вообще говоря, из приведенного выше неформального толкования понятия алгоритма. Сформулируем эти требования в виде перечня свойств, которым должны удовлетворять алгоритмы, адресуемые заданному исполнителю.
1. Одно из первых требований, которое предъявляется к алгоритму, состоит в том, что описываемый процесс должен быть разбит на последовательность отдельных шагов. Возникающая в результате такого разбиения запись представляет собой упорядоченную совокупность четко разделенных друг от друга предписаний (директив, команд, операторов), образующих прерывную (или, как говорят, дискретную) структуру алгоритма. Только выполнив требования одного предписания, можно приступить к выполнению следующего. Дискретная структура алгоритмической записи может. Например, подчеркиваться сквозной нумерацией отдельных команд алгоритма, хотя это требование не является обязательным. Рассмотренное свойство алгоритмов называют дискретностью.
2. Используемые на практике алгоритмы составляются с ориентацией на определенного исполнителя. Чтобы составить для него алгоритм, нужно знать, какие команды этот исполнитель может понять и исполнить, а какие - не может. Мы знаем, что у каждого исполнителя имеется своя система команд. Очевидно, составляя запись алгоритма для определенного исполнителя, можно использовать лишь те команды, которые имеются в его СКИ. Это свойство алгоритмов будем называть понятностью.
3. Будучи понятным, алгоритм не должен содержать предписаний, смысл которых может восприниматься неоднозначно, т.е. одна и та же команда, будучи понятна разным исполнителям, после исполнения каждым из них должна давать одинаковый результат.
Запись алгоритма должна быть настолько четкой, полной и продуманной в деталях, чтобы у исполнителя не могло возникнуть потребности в принятии решений, не предусмотренных составителем алгоритма.
Говоря иначе, алгоритм не должен оставлять места для произвола исполнителя. Кроме того, в алгоритмах недопустимы также ситуации, когда после выполнения очередной команды алгоритма исполнителю неясно, какая из команд алгоритма должна выполняться на следующем шаге.
Отмеченное свойства алгоритмов называют определенностью или детерминированностью.
4. Обязательное требование к алгоритмам - результативность. Смысл этого требования состоит в том, что при точном исполнении всех предписаний алгоритма процесс должен прекратиться за конечное число шагов и при этом должен получиться определенный результат. Вывод о том, что решения не существует - тоже результат.
5. Наиболее распространены алгоритмы, обеспечивающие решение не одной конкретной задачи, а некоторого класса задач данного типа. Это свойство алгоритма называют массовостью.
В простейшем случае массовость обеспечивает возможность использования различных исходных данных.
СВОЙСТВА СИМВОЛОВ
В Лиспе могут быть определены, так называемые, свойства символов. Список свойств имеет вид:
(имя_свойства1 значение1 имя_свойства2 значение2 . .. имя_свойстваN значениеN).
Присваивание нового свойства или изменение значения существующего осуществляется с помощью функции PUTPROP (или просто PUT):
(PUTPROP символ свойство значение).
Выяснить значение свойства, связанного с символом, можно с помощью функции GET:
(GET символ свойство).
С использованием этой функции можно также присваивать свойства символам:
(SETF (GET символ свойство) значение).
Свойства символов глобальны Эта конструкция языка Лисп полезна во многих типичных случаях представления данных, в том числе семантических сетей, фреймов и объектов объектно-ориентированного программирования.
ТЕХНИКА СТОХАСТИЧЕСКОГО МОДЕЛИРОВАНИЯ
Понятие «случайный» - одно из самых фундаментальных как в математике, так и в повседневной жизни. Моделирование случайных процессов - мощнейшее направление в современном математическом моделировании.
Событие называется случайным, если оно достоверно непредсказуемо. Случайность окружает наш мир и чаще всего играет отрицательную роль в нашей жизни. Однако есть обстоятельства, в которых случайность может оказаться полезной.
В сложных вычислениях, когда искомый результат зависит от результатов многих факторов, моделей и измерений, можно сократить объем вычислений за счет случайных значений значащих цифр. Из теории эволюции следует, что случайность проявляет себя как конструктивный, позитивный фактор. В частности, естественный отбор реализует как бы метод проб и ошибок, отбирая в процессе развития особи с наиболее целесообразными свойствами организма. Далее случайность проявляется в множественности ее результатов, обеспечивая гибкость реакции популяции на изменения внешней среды.
В силу сказанного имеет смысл положить случайность в основу методов получения решения посредством проб и ошибок, путем случайного поиска.
Отметим, что выше, приведя пример имитационного моделирования - игру «Жизнь», мы уже имели по сути дела стохастическую модель. В данном параграфе обсудим методологию такого моделирования более детально.
Итак, пусть в функционале модели значения некоторых входных параметров определены лишь в вероятностном смысле. В этом случае значительно меняется сам стиль работы с моделью.
При серьезном рассмотрении в обиходе появляются слова «распределение вероятностей», «достоверность», «статистическая выборка», «случайный процесс» и т.д.
При компьютерном математическом моделировании случайных процессов нельзя обойтись без наборов, так называемых, случайных чисел, удовлетворяющих заданному закону распределения. На самом деле эти числа генерирует компьютер по определенному алгоритму, т.е. они не являются вполне случайными хотя бы потому, что при повторном запуске программы с теми же параметрами последовательность повторится; такие числа называют «псевдослучайными».
Рассмотрим вначале генерацию чисел равновероятно распределенных на некотором отрезке. Большинство программ - генераторов случайных чисел - выдают последовательность, в которой предыдущее число используется для нахождения последующего. Первое из них - начальное значение. Все генераторы случайных чисел дают последовательности, повторяющиеся после некоторого количества членов, называемого периодом, что связано с конечной длиной машинного слова. Самый простой и наиболее распространенный метод - метод вычетов, или линейный конгруэнтный метод, в котором очередное случайное число xn определяется «отображением»
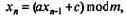
где a, с, m
- натуральные числа, mod - так называемая, функция деления по модулю (остаток от деления одного числа на другое по модулю). Наибольший возможный период датчика (7.69) равен т; однако, он зависит от а и с.
Ясно, что чем больше период, тем лучше; однако реально наибольшее m ограничено разрядной сеткой ЭВМ. В любом случае используемая в конкретной задаче выборка случайных чисел должна быть короче периода, иначе задача будет решена неверно. Заметим, что обычно генераторы выдают отношение

Вопрос о случайности конечной последовательности чисел гораздо сложнее, чем выглядит на первый взгляд Существует несколько статистических критериев случайности, но все они не дают исчерпывающего ответа. Так, последовательно генерируемые псевдослучайные числа могут появляться не идеально равномерно, а проявлять тенденцию к образованию групп (т е. коррелировать) Один из тестов на равномерность состоит в делении отрезка [0, 1] на М
равных частей - «корзин», и помещения каждого нового случайного числа в соответствующую «корзину». В итоге получается гистограмма, в которой высота каждого столбика пропорциональна количеству попавших в «корзину» случайных чисел (рис. 7.54).
Рис. 7.54. Вид гистограммы для равномерно распределенных на отрезке [0,1] чисел при достаточно большой выборке
Понятно, что при большом числе испытаний высоты столбиков должны быть почти одинаковыми. Однако, этот критерий является необходимым, но не достаточным; например, он «не замечает» даже очень короткой периодичности Для не слишком требовательного пользователя обычно достаточны возможности датчика (генератора) случайных чисел, встроенного в большинство языков программирования. Так, в PASCAL есть функция random, значения которой - случайные числа из диапазона [0, 1). Ее использованию обычно предшествует использование процедуры randomize, служащей для начальной «настройки» датчика, т.е. получения при каждом из обращений к датчику разных последовательностей случайных чисел. Для задач, решение которых требует очень длинных некоррелированных последовательностей, вопрос осложняется и требует нестандартных решений Равномерно распределенные случайные числа - простейший случай Располагая датчиком случайных
чисел, генерирующим числа r Î [0, 1], легко получить числа из произвольного интервала [а, b].
X = a + (b - a)•r.
Более сложные распределения часто строятся с помощью распределения равномерного. Упомянем здесь лишь один достаточно универсальный метод Неймана (часто называемый также методом отбора-отказа), в основе которого лежит простое геометрическое соображение. Допустим, что необходимо генерировать случайные числа с некоторой нормированной функцией распределения f(x) на интервале [а, b].
Введем положительно определенную функцию сравнения w(x) такую, что w(x) = const и w(x) > f(x) на [а, b] (обычно w(x) равно максимальному значению f(x) на [а, b]). Поскольку площадь под кривой f(x) равна для интервала [х, х + dx] вероятности попадания х
в этот интервал, можно следовать процедуре проб и ошибок. Генерируем два случайных числа, определяющих равновероятные координаты в прямоугольнике A BCD с помощью датчика равномерно распределенных случайных чисел:
x = a + (b - a)•r, y = w•r
и если точка М(х, у) не попадает под кривую f(x), мы ее отбрасываем, а если попадает - оставляем (рис. 7.55).При этом множество координат х оставленных точек оказывается распределенным в соответствии с плотностью вероятности
f(x).
Рис. 7.55. Метод отбора-отказа. Функция w(x) = fmax
Этот метод для ряда распределений не самый эффективный, но он универсален, прост и понятен. Эффективен он тогда, когда функция сравнения w(x) близка к f(х). Заметим, что никто не заставляет нас брать w(x)= const на всем промежутке [а, b]. Если f(x) имеет быстро спадающие «крылья», то разумнее взять w(x) в виде ступенчатой
функции.
ТЕХНОЛОГИЯ ПРОЕКТИРОВАНИЯ КОМПЬЮТЕРНЫХ ТЕСТОВ ПРЕДМЕТНОЙ ОБЛАСТИ
Компьютеры в обучении - вопрос, требующий отдельного рассмотрения. Отметим лишь, что различные варианты АОС (автоматизированных обучающих систем) вобрали в себя лучшие достижения компьютерных технологий и стали широко популярными не только в учебных заведениях, но и при подготовке персонала в промышленности, различных социальных сферах, военном деле и т д.
Обучение - многогранный процесс, и контроль знаний - лишь одна из его сторон. Однако именно в ней компьютерные технологии продвинулись максимально далеко, и среди них тестирование занимает ведущую роль. В ряде стран тестирование потеснило традиционные формы контроля - устные и письменные экзамены и собеседования.
По-видимому, многие преподаватели уже прошли через некоторую эйфорию при создании тестов и поняли, что это - весьма непростое дело. Куча бессистемно надерганных вопросов и ответов - далеко еще не тест. Оказывается, что для создания адекватного и эффективного теста нужно затратить много труда. Компьютер может оказать в этом деле немалую помощь.
Существует специальная теория тестирования, оперирующая понятиями надежность, валидность, матрица покрытия и т.д., не специфических именно для компьютерных тестов. Здесь мы не будем в нее углубляться, сосредоточившись в основном на технологических аспектах.
Широкое распространение в настоящее время получают инструментальные авторские системы по созданию педагогических средств: обучающих программ, электронных учебников, компьютерных тестов. Особую актуальность для преподавателей школ и вузов приобретают программы для создания компьютерных тестов - тестовые оболочки. Подобных программных средств существует множество и программисты-разработчики готовы строить новые варианты, так называемых, авторских систем. Однако широкое распространение этих программных средств сдерживается отсутствием простых и нетрудоемкнх методик составления тестовых заданий, с помощью которых можно «начинять» оболочки. В настоящем разделе представлены некоторые подходы к разработке компьютерных тестов.
Проектирование модели знаний.
Эксперты чаще используют метод нисходящего проектирования модели знаний (технология «сверху - вниз»). Вначале строится генеральное содержание предметной области с разбивкой на укрупненные модули (разделы). Затем проводится детализация модулей на элементарные подмодули, которые, в свою очередь, наполняются педагогическим содержанием.
Другой метод проектирования «снизу - вверх» (от частного к общему) в большинстве случаев реализуется группой экспертов для разработки модели знаний сложной и объемной предметной области, или для нескольких, близких по структуре и содержанию, предметных областей.
Каждый модуль предполагает входящую информацию, состоящую из набора необходимых понятий из других модулей и предметных областей, а на выходе создает совокупность новых понятий, знаний, описанных в данном модуле.
Модуль может содержать подмодули. Элементарный подмодуль - неделимый элемент знания - может быть представлен в виде базы данных, базы знаний, информационной модели. Понятия и отношения между ними представляют семантический граф.
Приведем пример элемента модуля знаний по теме «Исследование графиков функций», рис. 2.29:
Рис. 2.29. Пример элемента модуля знаний
Модульное представление знаний помогает:
• организовать четкую систему контроля с помощью компьютерного тестирования, поскольку допускает промежуточный контроль (тестирование) каждого модуля, итоговый по всем модулям и их взаимосвязям, а также эффективно использовать методику «черного ящика»;
• осуществлять наполнение каждого модуля педагогическим содержанием;
• выявить и учитывать семантические связи модулей и их отношения с другими предметными областями.
Этапы разработки компьютерных тестов.
Можно выделить два принципиальных способа контроля (тестирования) некоторой системы:
1) метод «белого ящика» - принцип тестирования экспертной модели знаний;
2) метод «черного ящика» - тестирование некоторой сложной системы по принципу контроля входных и выходных данных (наиболее подходит для компьютерного тестирования).
Введем ряд определений и понятий.
Тестирование - процесс оценки соответствия личностной модели знаний ученика экспертной модели знаний. Главная цель тестирования - обнаружение несоответствия этих моделей (а не измерение уровня знаний), оценка уровня их несоответствия.
Тестирование проводится с помощью специальных тестов, состоящих из заданного набора тестовых заданий.
Тестовое задание - четкое и ясное задание по предметной области, требующее однозначного ответа или выполнения определенного алгоритма действий.
Тест - набор взаимосвязанных тестовых заданий, позволяющих оценить соответствие знании ученика экспертной модели знаний предметной области.
Тестовое пространство
- множество тестовых заданий по всем модулям экспертной модели знании.
Класс эквивалентности - множество тестовых заданий, таких, что выполнение одного из них учеником гарантирует выполнение других.
Полный тест - подмножество тестового пространства, обеспечивающего объективную оценку соответствия между личностной моделью и экспертной моделью знаний.
Эффективный тест - оптимальный по объему полный тест.
Самой сложной задачей эксперта по контролю является задача разработки тестов, которые позволяют максимально объективно оценить уровень соответствия или несоответствия личностной модели знании ученика и экспертной модели.
Подбор тестовых заданий осуществляется экспертами-педагогами методологией «белого ящика», а их пригодность оценивают с помощью «черного ящика», рис. 2.30.
Оценка соответствия
Рис. 2.30. Схема создания тестовых заданий
Самый простой способ составления тестовых заданий - формирование вопросов к понятиям, составляющим узлы семантического графа, разработка упражнений, требующих для выполнения знания свойств выбранного понятия. Более сложным этапом является разработка тестовых заданий, определяющих отношения между понятиями. Еще более глубокий уровень заданий связан с подбором тестов, выявляющих связь понятий между отдельными модулями.
Множество тестовых заданий (тестовое пространство), вообще говоря, согласно принципу исчерпывающего тестирования, может быть бесконечным.
Однако в каждом реальном случае существует конечное подмножество тестовых заданий, использование которых позволяет с большой вероятностной точностью оценить соответствие знаний ученика заданным критериям по экспертной модели знаний (полный тест).
Из полного теста можно выделить эффективный тест (оптимальный по объему набор тестовых заданий, гарантирующий оценку личностной модели ученика заданным критериям). Выбор эффективного теста зависит от удачного разбиения тестового пространства на классы эквивалентности, пограничные условия, создания тестов на покрытие путей и логических связей между понятиями и модулями.
В дальнейшем необходим тестовый эксперимент на группе учащихся, который позволит провести корректировку и доводку теста до вида эксплуатации (методика черного ящика).
Таким образом, построение компьютерных тестов можно осуществлять в следующей последовательности:
• формализация экспертной целевой модели знаний;
• нисходящее (или снизу - вверх) проектирование тестового пространства;
• формирование и наполнение тестовых заданий;
• формирование полного компьютерного теста;
• тестовый эксперимент;
• выбор эффективного теста;
• анализ, корректировка и доводка теста до вида эксплуатации.
ТЕКСТОВЫЕ РЕДАКТОРЫ
Программы-текстовые редакторы предназначены для подготовки текстовых материалов на компьютере.
Поскольку текстовые материалы бывают различной сложности по набору и верстке, существуют и развиваются различные программы обработки текстов. Их можно классифицировать по уровням требований к обработке текстов. Перечислим наиболее популярные из них.
А. Программы для набора и обработки простых текстов:
Lexicon
Refis
Norton Editor
MultiEdit
Word 4.0 и 5.0 и др.
Б. Программы для набора сложных текстов:
ChiWriter
TechWord
Word 5.5, 6.0 и 7.0
Word for Windows 1.1 и
2.2
WordPerfect
TeX, LaTex
и др.
Каждый текстовый редактор имеет свои технические требования к составу и конфигурации компьютерной техники.
Для набора простого текста достаточно иметь
• персональный компьютер IBM PC/XT, AT (или совместимые с ними) с емкостью оперативной памяти 640 кбайт;
• дисплей монохромный CGA, EGA или Hercules 14.
Для набора сложных текстов, содержащих формулы, таблицы, схемы необходимо иметь
• персональный компьютер IBM PC/AT 286 (или совместимые с ним), с емкостью оперативной памяти 1 Мбайт;
• дисплей монохромный CGA, EGA или Hercules 14;
• накопитель на жестком магнитном диске (30 - 40 Мбайт);
• матричный 9- или 24-игольчатый принтер, струйный или лазерный принтер;
• мышь.
Для подготовки черно-белых иллюстраций, логотипов, обложек, титулов, разработки шрифтов необходимо иметь
• персональный компьютер IBM PC/AT 386/486 (или совместимые с ним) с емкостью оперативной памяти 4 Мбайт;
• дисплей цветной VGA, SVGA 14/15;
• накопитель на жестком магнитном диске (более 80 Мбайт);
• лазерный принтер;
• сканер;
• мышь.
Разумеется, подходят не только компьютеры IBM-совместимые, но и другие (например, Macintosh); разные модели IBM указаны лишь поскольку они наиболее распространены для ориентации по уровню требований.
Разработчики программ текстовых редакторов стараются предусмотреть в них предоставление пользователю всех необходимых операций и сервисных возможностей для эффективной обработки текстов Выделим главные из них:
· набор текста в интерактивном режиме;
· редактирование текста;
· работа с фрагментами текста (копирование, перемещение, удаление и т.п.);
· форматирование текста ( установка абзаца, перенос, выравнивание границ строки и т.п);
· работа с несколькими текстами одновременно посредством многооконного принципа;
· файловая организация работы с текстами и взаимодействие с операционной системой;
· импорт/экспорт текстов из одного формата в другой, в другие прикладные системы;
· работа с разными шрифтами;
· работа со спецсимволами (математические знаки, индексы и т.п.);
· работа с иллюстративным материалом (таблицы, схемы, формулы и пр.);
· проверка правописания;
· поиск и замена фрагментов текста.
Рассмотрим для примера меню популярного в России текстового редактора Лексикон, рис. 2.14.

Рис. 2.14. Главное меню и строка статуса текстового редактора Лексикон
Здесь верхняя строка одновременно является строкой комментариев к пунктам меню, и пользователю легко понять их назначение. Функциональные клавиши имеют достаточно стандартные назначения. Например, F1 - помощь, F9 - переключение с русского на латинский режимы, F10 - выход в меню.
Меню позволяет осуществить настройку редактора на подготовку того или иного документа, связаться с операционной системой. Правила набора, редактирования текста просты и очевидны.
ТЕЛЕКОММУНИКАЦИИ КАК СРЕДСТВО ОБРАЗОВАТЕЛЬНЫХ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
Компьютерные телекоммуникации все настойчивее проникают в различные сферы жизни современного общества: бизнес, финансы, средства массовой информации, науку и образование.
Несмотря на то что Россия занимает сейчас 37-е место в мире по уровню телефонизации (являющейся одним из важнейших факторов, обусловливающих развитие компьютерных телекоммуникаций в стране), за последние 2-3 года российские пользователи персональных ЭВМ получили доступ ко множеству зарубежных телекоммуникационных сетей.
На общем фоне развития телекоммуникаций в нашей стране постепенно проявляется и становится заметным процесс внедрения компьютерных телекоммуникаций в сферу народного образования, и, прежде всего, в жизнь современной школы. Десятки тысяч школ за рубежом и сотни школ в нашей стране за последние 5-7 лет начали использовать возможности современных телекоммуникаций непосредственно в учебной работе.
Особенно стремятся участвовать в этом процессе школы из «глубинки», где уже есть современная телефонная сеть. но по-прежнему нет доступа к современной оперативной информации по различным отраслям знаний.
Некоторые учителя используют телекоммуникации преимущественно для внеклассной работы с учащимися по отдельным экспериментальным проектам. Однако уже сейчас многие школы за рубежом используют компьютерные телекоммуникации непосредственно на уроках в условиях реального учебного процесса, постепенно подготавливая учащихся к жизни в информационном обществе. Компьютерные телекоммуникации начинают постепенно осознаваться многими педагогами как один из инструментов познания окружающего мира. Инструмент этот настолько мощный, что вместе с ним в школу приходят новые формы и методы обучения, новая идеология глобального мышления.
Компьютерные телекоммуникации - интенсивно развивающийся вид информационных технологий, использующий глобальные компьютерные сети, - обещают совершить переворот в методах и формах обучения. Простейший вид телекоммуникаций - электронная почта - уже сейчас, с минимальными затратами, с успехом может быть использован в учебном процессе каждой школы.
Учебное значение электронной почты состоит в том, что она
• стимулирует и облегчает обмен опытом преподавателей различных предметов;
• повышает интерес учащихся к учебному курсу, в котором используется;
• расширяет коммуникативную практику учащихся, помогает в совершенствовании письменной речи;
• делает возможным использование новых методических приемов, основанных на сопоставлении собственных данных учащихся и тех, которые получены по электронной почте.
Использование электронной почты в обучении обычно протекает в форме телекоммуникационных проектов. Учебный телекоммуникационный проект посвящается определенной теме, включает разнообразные виды деятельности учащихся по подготовке и передаче, а также получению и анализу учебной информации с помощью средств компьютерных телекоммуникации, и охватывает по времени от нескольких дней до нескольких месяцев.
Простые телекоммуникационные проекты могут выполняться двумя классами учащихся под непосредственным руководством учителей и проходят в форме неструктурированной коллективной переписки. Сложные длительные проекты, в которых участвуют десятки и сотни классов, требуют участия в проектах координаторов и методистов, руководящих ходом телекоммуникаций, добивающихся согласованности содержания и сроков отправки корреспонденции. Большие проекты проводятся в специализированных учебных компьютерных сетях (США, Канады, Великобритании и т.д.).
В России учебные компьютерные сети еще не развиты, и в настоящий момент российское образование делает первые шаги к учебному использованию компьютерной электронной почты как средству управления учебной мотивацией. Публикация с помощью электронной почты оказывается оперативной целью овладения компьютером, проведения наблюдений и измерений, коллективной деятельности учащихся.
Во многих школах России имеется опыт следующего использования электронной почты:
• для обмена опытом педагогов, проводящих различные учебные курсы;
• для обмена между учащимися коллективными сообщениями следующих типов:
- письма общего характера (письмо-представление, рассказ о своем городе, о школьных друзьях и о спортивных достижениях, рассказ о домашних животных, поздравления с праздниками и др.):
- писем-отчетов о проведенных исследованиях и выполненных проектах;
- датаграфических и фенологических наблюдений за погодой;
•для проведения компьютерных телекоммуникационных викторин;
• для «распределенного» выполнения исследований ( лабораторные исследования и измерения выполняет один из классов, а остальные классы обобщают присланные им данные измерений и результаты наблюдений).
В образовательной практике могут найти применение все основные виды компьютерных телекоммуникаций:
• электронная почта;
• списки рассылки (list-серверы);
• электронные доски объявлений (BBS);
• телеконференции;
• Gopher- и WWW-серверы.
Там же находят применения различные информационные технологии общения, в частности:
• общение многих со многими;
• общение, не ограниченное географическими расстояниями;
• общение, не ограниченное временными рамками;
• общение на основе текста, а не речи.
Установлено, что общение, опосредованное компьютером, влияет на основные характеристики общения людей с помощью компьютерных сетей.
Комплексное использование информационных и коммуникативных возможностей Internet обладает очень большими потенциальными возможностями в образовании. Возможности этой системы для поддержки свободного обмена информацией поразительны и практически безграничны. Рассмотрим основные идеи использования телекоммуникационных средств в образовательном контексте, основанные на классификации большого количества файлов, полученных в результате работы в Internet. Данный материал может помочь спланировать эффективное использование телекоммуникаций в обучении, полностью интегрированное с изучаемым учебным курсом.
ТИПЫ ДАННЫХ И ОПЕРАЦИИ В ЯЗЫКЕ СИ. ВЫРАЖЕНИЯ
Типы данных.
Программа на процедурных языках, к которым относится Си, представляет собой описание операций над величинами различных типов. Тип определяет множество значений, которые может принимать величина, и множество операций, в которых она может участвовать.
В языке Си типы связаны с именами (идентификаторами) величин, т. е. с переменными. С переменной в языке Си связывается ячейка памяти. Тип переменной задает размер ячейки, способ кодирования ее содержимого, допустимые преобразования над значением данной переменной. Все переменные должны быть описаны до их использования. Каждая переменная должна быть описана только один раз.
Описание состоит из спецификатора типа и следующего за ним списка переменных. Переменные в списке разделяются запятыми. В конце описания ставится точка с запятой.
Примеры описаний:
char a,b; /* Переменные а и b имеют тип
char */ int х; /* Переменная х - типа int
*/ char sym; /" Описаны переменные sym типа char;
*/ int count.num; /* num и count типа int */
Переменным могут быть присвоены начальные значения внутри их описаний. Если за именем переменной следует знак равенства и константа, то эта константа служит в качестве инициализатора.
Примеры: char backch = '\0';
int i = 0;
Рассмотрим основные типы в языке Си.
int - целый ("integer"). Значения этого типа - целые числа из некоторого ограниченного диапазона (обычно от- 32768 до 32767). Диапазон определяется размером ячейки для типа и зависит от конкретного компьютера. Кроме того, имеются служебные слова, которые можно использовать с типом int: short int («short integer» - «короткое целое»), unsigned int («unsigned integer» - «целое без знака»), long int («длинное целое»), которые сокращают или, наоборот, расширяют диапазон представления чисел.
char - символьный («character»). Допустимое значение для этого типа — один символ (не путать с текстом!). Символ записывается в апострофах.
Примеры:
'х"2"?'
В памяти компьютера символ занимает один байт.
Фактически хранится не символ, а число - код символа (от 0 до 255). В специальных таблицах кодировки указываются все допустимые символы и соответствующие им коды.
В языке Си разрешается использовать тип char как числовой, т. е. производить операции с кодом символа, применяя при этом спецификатор целого типа в скобках - (int).
float - вещественный (с плавающей точкой). Значения этого типа - числа, но, в отличии от char и int, не обязательно целые.
Примеры:
12.87 -316.12 -3.345е5 12.345e-15
double - вещественные числа двойной точности. Этот тип аналогичен типу float, но имеет значительно больший диапазон значений (например, для системы программирования Borland-C от 1.7Е-308 до 1.7Е+308 вместо диапазона от 3.4Е-38 до 3.4Е+38 для типа float). Однако увеличение диапазона и точности представления чисел ведет к снижению скорости выполнения программ и неэкономному использованию оперативной памяти компьютера.
Обратите внимание на отсутствие в этом списке строкового типа. В языке Си нет специального типа, который можно было бы использовать для описания строк. Вместо этого строки представляются в виде массива элементов типа char. Это означает, что символы в строке будут располагаться в соседних ячейках памяти.
Необходимо отметить, что последним элементом массива является символ \0. Это «нуль-символ», и в языке Си он используется для того, чтобы отмечать конец строки. Нуль-символ не цифра 0; он не выводится на печать и в таблице кодов ASCII имеет номер 0. Наличие нуль-символа означает, что количество ячеек массива должно быть. по крайней мере, на одну больше, чем число символов, которые необходимо размещать в памяти.
Приведем пример использования строк.
Программа 84
# include<stdio.h> main()
{
char string[31] ;
scanf("%s",string) ;
printf("%s",string);
}
В этом примере описан массив из 31 ячейки памяти, в 30 из которых можно поместить один элемент типа char. Он вводится при вызове функции scanf("%s",string); "&"отсутствует при указании массива символов.
Указатели. Указатель - некоторое символическое представление адреса ячейки памяти, отведенной для переменной.
Например, &name - указатель на переменную name;
Здесь & - операция получения адреса. Фактический адрес - это число, а символическое представление адреса &name является константой типа «указатель».
В языке Си имеются и переменные типа указатель. Точно так же, как значением переменной типа char является символ, а значением переменной типа int - целое число, значением переменной типа указатель служит адрес некоторой величины.
Если мы дадим указателю имя ptr, то сможем написать такой оператор:
ptr = &name;/* присваивает адрес name переменной ptr */
Мы говорим в этом случае, что prt «указатель на» name. Различие между двумя формами записи: ptr и &name - в том, что prt - это переменная, в то время как &name - константа. В случае необходимости можно сделать так, чтобы переменная ptr указывала на какой-нибудь другой объект:
ptr = &bah; /* ptr указывает на bah, а не на name */
Теперь значением переменной prt является адрес переменной bah. Предположим, мы знаем, что в переменной ptr содержится ссылка на переменную bah. Тогда для доступа к значению этой переменной можно воспользоваться операцией «косвенной адресации» * :
val = *ptr; /* определение значения, на которое указывает ptr */ Последние два оператора, взятые вместе, эквивалентны следующему:
val = bah;
Итак, когда за знаком &
следует имя переменной, результатом операции является адрес указанной переменной; &nurse дает адрес переменной nurse; когда за знаком * следует указатель на переменную, результатом операции является величина, помещенная в ячейку памяти с указанным адресом.
Пример: nurse = 22;
ptr = &nuse; /* указатель на nurse */
val = *ptr;
Результат- присваивание значения 22 переменной val.
Недостаточно сказать, что некоторая переменная является указателем. Кроме этого необходимо сообщить, на переменную какого типа ссылается данный указатель. Причина заключается в том, что переменные разных типов занимают различное число ячеек памяти, в то время как для некоторых операций, связанных с указателями, требуется знать объем отведенной памяти.
Примеры
правильного описания указателей: int *pi; char *pc;
Спецификация типа задает тип переменной, на которую ссылается указатель, а символ * определяет саму переменную как указатель. Описание вида int *pi; говорит, что pi - это указатель и что *pi - величина типа int.
В языке Си предусмотрена возможность определения имен типов данных. Любому типу данных с помощью определения typedef можно присвоить имя и использовать это имя в дальнейшем при описании объектов.
Формат: typedef <старый тип> <новый тип> Пример: typedef long LARGE; /* определяется тип large, эквивалентный типу long */
Имена производного типа рекомендуется записывать прописными буквами, чтобы они выделялись в тексте программы.
Определение typedef не вводит каких-либо новых типов, а только добавляет новое имя для уже существующего типа. Описанные таким способом переменные обладают точно теми же свойствами, что и переменные, описанные явно. Переименование типов используется для введения осмысленных или сокращенных имен типов, что повышает понятность программ, и для улучшения переносимости программ (имена одного типа данных могут различаться на разных компьютерах).
Операции. Язык Си отличается большим разнообразием операций (более 40). Здесь мы рассмотрим лишь основные из них, табл. 3.3.
Арифметические операции. К ним относят
• сложение(+),
• вычитание (бинарное) (-),
• умножение (*),
• деление (/),
• остаток от деления нацело (%),
• вычитание (унарное) (-) .
В языке Си принято правило: если делимое и делитель имеют тип int, то деление производится нацело, т е. дробная часть результата отбрасывается.
Как обычно, в выражениях операции умножения, деления и нахождения остатка выполняются раньше сложения и вычитания. Для изменения порядка действий используют скобки.
Программа 85
#include<stdio.h>
main()
(
int s;
5 = -3 + 4 * 5 - 6; printf("%d\n",s);
s = -3 + 4%5 - 6; printf("%d\n",s);
s = -3 * 4% - 6/5; printf("%d\n",s);
s= (7 + 6)%5/2; printf("%d\n",s);
}
Результат выполнения программы: 11 1 0 1
Таблица 3.3 Старшинство и порядок выполнения операций
|
Приоритет |
Операция |
Название |
Порядок выполнения |
||
|
Высший |
() [] ++ -- (тип) * |
Круглые скобки Квадратные скобки Увеличение Уменьшение Приведение Содержимое |
Слева направо Слева направо Справа налево Справа налево Справа налево Справа налево |
||
|
1 |
& - ! /~ sizeof * |
Адрес Унарный минус Логическое «НЕ» Инверсия битов Размер объекта Умножение |
Справа налево Справа налево Справа налево Справа налево Справа налево Слева направо |
||
|
2 |
\ % |
Деление Остаток |
Слева направо Слева направо |
||
|
3 |
+ - |
Сложение Вычитание |
Слева направо Слева направо |
||
|
4 |
» « > |
Сдвиг вправо Сдвиг влево Больше |
Слева направо Слева направо Слева направо |
||
|
5 |
>= < <= |
Больше или равно Меньше Меньше или равно |
Слева направо Слева направо Слева направо |
||
|
6 |
= = != |
Равно Не равно |
Слева направо Слева направо |
||
|
7 |
& |
Битовое «И» |
Слева направо |
||
|
8 |
~ |
Битовое исключающее «ИЛИ» |
Слева направо |
||
|
9 |
| |
Битовое «ИЛИ» |
Слева направо |
||
|
10 |
&& |
Логическое «И» |
Слева направо |
||
|
11 |
|| = += |
Логическое «ИЛИ» Операция присвания Справа налево |
Слева направо Справа налево |
||
|
12 |
- = *= /= %= |
Специальная форма операции присваивания |
Справа налево Справа налево Справа налево Справа налево |
||
Для этого обычно выполняются оператор присваивания вида: s= s + 1;
В языке Си для этих действий существуют специальные операции:
• увеличение (+ +),
• уменьшение (--).
Следующие записи на языке Си являются эквивалентными:
i=i+l и i++; j=j-1 и j--;.
Символы "++" или "- -" записывается после имени переменной или перед ним.
Пример:
s + +; /* s увеличить на единицу
*/ t - -; /* t уменьшить на единицу
*/ + + а; /* а увеличить на единицу
*/ --b; /* b уменьшить на единицу */
Как и обычные присваивания, увеличение и уменьшение можно использовать в выражениях. При этом существенно, с какой стороны от имени стоит знак "+ +"или "- -". Если знак стоит перед переменной (в этом случае говорят о префиксной форме операции), то сначала выполняется увеличение (уменьшение) значения переменной, а лишь затем полученный результат используется в выражении. Если же знак стоит после переменной (постфиксная форма операции), то в выражении используется старое значение переменной, которое затем изменяется.
Пример:
inti,j,s;
i = j = 2; /* i и j получают значение 2 */
s = (i++) + (++J);
После выполнения этих действий переменные имеют такие значения:
i=3;j=3;s=5.
Операции увеличения ++ и уменьшения - - можно применять топько к переменным, выражения типа s=(i+j)++ являются незаконными. Кроме того, не рекомендуется:
1) применять операции увеличения или уменьшения к переменной, присутствующей в более чем одном аргументе функции,
2) применять операции увеличения или уменьшения к переменной, которая входит в выражение более одного раза.
Операции отношения и логические операции
|
Больше или равно |
>= |
|
Больше |
> |
|
Меньше или равно |
<= |
|
Меньше |
< |
|
Равно |
== |
|
Неравно |
!= |
|
Логическое «и» |
&& |
|
Логическое «или» |
|| |
|
Отрицание «не» |
! |
Логическое значение «ложь» представляется целым нулевым значением, а значение «истина» представляется любым ненулевым значением
Выражения, связанные логическими операциями && и ||, вычисляются слева направо, причем вычисление значения выражения прекращается сразу же, как только становится ясно, будет ли результат истинен или ложен.
Старшинство операции && выше, чем у операции ||.
Программа 86
#include<stdio.h>
main()
(
int x, у, z;
x=l; y=l; z=0; x=x&&y||z; printf("%d\n",x);
x=x|| !y&&z; printf("%d\n",x) ;
x=y=l; z=x++-l; printf("%d\n",x);printf("%d\n",z) ;
z+=-x++ + ++y; printf("%d\n",x) ; printf("%d\n",z);
z=x/++x; printf("%d\n",x); printf("%d\n",z) ;
}
Результат выполнения программы: 1 1 2 0 3 0 4 1
Битовые операции
|
Битовое «и» Битовое «или» Битовое исключающее «или» Сдвиг влево Сдвиг вправо Инверсия битов (унарная операция) |
& | ~ « » \ ~ |
#include<stdio.h>
main()
(
int у, х, z, k;
x=03; y=02; z=01; k=x|y&z; printf("%d\n",k) ;
k=x|y&~z; printf("%d\n",k) ;
k=x^y&~z; printf("%d\n",k) ;
k=x&y&&z; printf("%d\n",k) ;
x=l; y=-l;
k=!x|x; printf("%d\n",k) ;
k=-x|x; printf("%d\n",k) ;
k=x^x; printf("%d\n",k) ;
x<<=3; printf("%d\n",x);
y<<=3; printf("%d\n",y);
y>>=3; printf("%d\n",y);
}
После выполнения программы получаем следующие результаты:
3 3 1 1 1 -1 0 8 -8 8 1 9 1
Выражения. Конструкции, включающие константы (литералы), переменные, знаки операции, скобки для управления порядком выполнения операций, обращения к функциям, называют выражениями.
Если в выражениях встречаются операнды различных типов, то они преобразуются к общему типу в соответствии с определенными правилами:
• переменные типа char интерпретируются как целые без знака (unsigned);
• переменные типа short автоматически преобразуются в int; если один из операндов имеет тип unsigned, то другой (другие) также преобразуется к типу unsigned и результат имеет тип unsigned;
• если один из операндов имеет тип int, то другой (другие) также преобразуется к типу int и результат имеет тип int;
• если один из операндов имеет тип char, то другой (другие) также преобразуется к типу char и результат имеет тип char;
• во время операции присваивания значение правой части преобразуется к типу левой части, который и становится типом результата;
• в процессе преобразования int в char лишние старшие 8 бит просто отбрасываются. Кроме того, существует возможность точно указывать требуемый тип данных, к которому необходимо привести некоторую величину (в скобках перед этой величиной). Скобки и имя типа вместе образуют операцию, называемую приведением типов.
Например: z=(int)x+(int)y;
ТИПЫ КОМПЬЮТЕРНЫХ ТЕСТОВ
В соответствии с моделью знаний, выделим три класса компьютерных тестов на знания, умения и навыки. Отметим, что типы компьютерных тестовых заданий определяются способами однозначного распознавания ответных действий тестируемого.
1.Типы тестовых заданий по блоку «знания» — вопросы альтернативные (требуют ответа да - нет);
• вопросы с выбором (ответ из набора вариантов);
• вопросы информативные на знание фактов (где, когда, сколько);
• вопросы на знание фактов, имеющих формализованную структуру (в виде информационной модели или схемы знаний);
• вопросы по темам, где имеются однозначные общепринятые знаковые модели:
математические формулы, законы, предикатные представления, таблицы;
• вопросы, ответы на которые можно контролировать по набору ключевых слов;
• вопросы, ответы на которые можно распознавать каким-либо методом однозначно.
2. Типы тестовых заданий по блоку «навыки» (распознание деятельности: манипуляции с клавиатурой; по конечному результату):
• задания на стандартные алгоритмы (альтернативные да - нет, выбор из набора вариантов);
• выполнение действия.
3. Типы тестовых заданий по блоку «умения». Те же самые, что для навыков, но используют нестандартные алгоритмы и задачи предметной области при контроле времени их решения:
• задания на нестандартные алгоритмы (альтернативные да - нет, выбор из набора вариантов);
• выполнение действия.
Выбор типов тестов определяется:
• особенностями инструментальных тестовых программ (тестовыми оболочками); .
• особенностями предметной области;
• опытом и мастерством экспертов.
ТИПЫ ОБУЧАЮЩИХ ПРОГРАММ
Основанием для классификации служат обычно особенности учебной деятельности обучаемых при работе с программами. Многие авторы выделяют четыре типа обучающих программ:
• тренировочные и контролирующие;
• наставнические;
• имитационные и моделирующие;
• развивающие игры.
Программы 1-го типа
(тренировочные) предназначены для закрепления умений и навыков. Предполагается, что теоретический материал уже изучен. Эти программы в случайной последовательности предлагают учащемуся вопросы и задачи и подсчитывают количество правильно и неправильно решенных задач (в случае правильного ответа может выдаваться поощряющая ученика реплика). При неправильном ответе ученик может получить помощь в виде подсказки.
Программы 2-го типа
(наставнические) предлагают ученикам теоретический материал для изучения. Задачи и вопросы служат в этих программах для организации человеко-машинного диалога, для управления ходом обучения. Так если ответы, даваемые учеником, неверны, программа может «откатиться назад» для повторного изучения теоретического материала.
Программы наставнического типа являются прямыми наследниками средств программированного обучения 60-х годов в том смысле, что основным теоретическим источником современного компьютерного или автоматизированного обучения следует считать программированное обучение. В публикациях зарубежных специалистов и сегодня под термином «программированное обучение» понимают современные компьютерные технологии. Одним из основоположников концепции программированного обучения является американский психолог Б.Ф.Скиннер.
Главным элементом программированного обучения является программа, понимаемая как упорядоченная последовательность рекомендаций (задач), которые передаются с помощью дидактической машины или программированного учебника и выполняются обучаемыми. Существует несколько известных разновидностей программированного обучения.
1.Линейное программированное обучение. Основатель - Б.Ф.Скиннер, профессор психологии Гарвардского университета, США.
Впервые выступил со своей концепцией в 1954 г. При ее создании Скиннер опирался на бихевиористскую психологию, в соответствии с которой обучение основано на принципе S - R, т.е. на появлении некоторых факторов (S - stimulus) и реакции на них (R - reaction). По этой концепции для любой реакции, соответственно усиленной, характерна склонность к повторению и закреплению. Поощрением для обучаемого является подтверждение программой каждого удачного шага, причем, учитывая простоту реакции, возможность совершения ошибки сводится к минимуму.
Линейная программа в понимании Скиннера характеризуется следующими особенностями:
• дидактический материал делится на незначительные дозы, называемые шагами, которые обучаемые преодолевают относительно легко, шаг за шагом;
• вопросы, содержащиеся в отдельных рамках программы, не должны быть очень трудными, чтобы обучаемые не потеряли интереса к работе;
• обучаемые сами дают ответы на вопросы, привлекая для этого необходимую информацию;
• в ходе обучения учащихся сразу же информируют о том, правильны или ошибочны их ответы;
• все обучаемые проходят по очереди все рамки программы, но каждый делает это в удобном ему темпе;
• во избежание механического запоминания информации одна и та же мысль повторяется в различных вариантах и нескольких рамках программы.
2. Разветвленная программа. Автор концепции разветвленного программирования - Норман А.Кроудер. Разветвленная программа основана на выборе одного правильного ответа из нескольких данных, она ориентирует на текст многократного выбора. По мнению автора, выбор правильных ответов требует от обучаемых больших умственных способностей, нежели припоминание какой-то информации. Непосредственное подтверждение правильности ответа он считает своеобразным типом обратной связи.
Вопросы, в понимании Кроудера, имеют целью
• проверить, знает ли ученик материал;
• в случае отрицательного ответа отсылать обучаемого к координирующим и соответственно обосновывающим ответ порциям информации;
• возможность закрепления основной информации с помощью рациональных упражнений;
• увеличение усилий обучаемого и одновременную ликвидацию механического обучения через многократное повторение информации;
• формирование требуемой мотивации обучаемого.
Если основой линейной программы является стремление избежать ошибок, то разветвленная программа не направлена на ликвидацию ошибок в процессе обучения; ошибки Кроудер трактует как возможность обнаружить недостатки в знаниях обучаемых, а также выяснить, какие проблемы обучаемые уяснили недостаточно; благодаря этому о его программе можно было бы сказать, что она сводится к «управлению процессом мышления», в то время как линейная программа основана на «управлении ответами».
Постепенно оба классических типа - линейное и разветвленное программированное обучение-уступили место смешанным формам.
По своей методической структуре педагогическое программное средство (ППС), реализующие программированный подход, характеризуются наличием следующих блоков:
• блока ориентировочной основы действий (ООД), содержащего текстово-графическое изложение теоретических основ некоторого раздела автоматизированного курса;
• контрольно-диагностического блока, контролирующего усвоение ООД и управляющего обучением;
• блока автоматизированного контроля знаний, формирующего итоговую оценку знаний учащегося.
Известно несколько видов организации программ наставнического типа, называемых также алгоритмами программированного обучения.
1. Последовательно-подготовительный алгоритм. Начальный элемент задания относительно прост, он подготавливает выполнение второго, более сложного, а тот, в свою очередь, третьего и т.д. Заключительные элементы имеют достаточно высокий уровень сложности.
2. Параллельно-подготовительный алгоритм. Начальные элементы заданий независимо один от другого подготавливают выполнение следующего за ним комплексного элемента высокого уровня.
3. Последовательно-корректирующий алгоритм. Начальные элементы задания имеют высокий уровень сложности, а каждый последующий элемент корректирует выполнение предыдущего, указывая, например, на противоречия, к которым приводят неправильные ответы.
4. Параллельно- корректирующий алгоритм. Обучаемому предлагается комплексный элемент высокого уровня, последующие элементы играют роль наводящих (подсказывающих), причем с разных позиций, независимо один от другого.
5. Алгоритм переноса. Приводятся два массива элементов A(N) и B(N). Ими могут быть понятия, отношения, действия, характеристики и т.д. Требуется установить логическое соответствие между ними.
6. Аналитический алгоритм. Предлагаются элементы A(N). Необходимо установить принадлежность каждого из них к одному из классов В(К).
7. Синтезирующий алгоритм. Элементы массива A(N) уже разбиты на подгруппы. Задача обучаемого - установить критерий, по которому осуществлялась классификация.
8. Алгоритм упорядочения.
Элементы массива A(N) необходимо упорядочить по некоторому указанному критерию В(К). Этот алгоритм требует для своего выполнения комплексной умственной деятельности.
Большинство инструментальных систем предоставляют преподавателю возможность составлять обучающие и контролирующие задания с различными типами ответов
1. С выборочным ответом. Обучаемому предлагается задание (вопрос) и набор (меню) готовых ответов, из которых он может сделать выбор правильного, по его мнению, ответа (утверждения).
Такой вариант задания наиболее удобен для машинной реализации, так как ЭВМ анализирует лишь номер, по которому легко определяет правильность ответа. На первый взгляд задания с выборочным ответом имеют ряд недостатков, а именно: обязательное предъявление верного ответа, возможность его угадывания, а значит, ограничение мыслительной деятельности обучаемого. Эти недостатки существенно снижаются путем правильного, творческого и остроумного применения различных принципов составления таких заданий.
Вероятность угадывания правильного ответа сводится к минимуму следующими простыми приемами:
• повторением аналогичного по смыслу вопроса в нескольких различных формах;
• увеличением числа элементов для выбора (при выборе из пяти ответов вероятность угадывания равна 0,2):
• увеличение числа верных ответов до двух или до нескольких пар. Подбирать ответы в заданиях необходимо таким образом, чтобы они были правдоподобными и равнопривлекательными.
2. С частично-конструируемьш ответом. Задания этого типа являются промежуточным и связующим звеном между заданиями с выборочным ответом и свободно-конструируемым. Частично-конструируемый ответ составляется из частей, предложенных преподавателем.
Эта форма используется для заданий по составлению определений законов, теорем, стандартных формулировок и т.д. В верный ответ входят, как правило, не все элементы задания, и порядок их выбора не является жестким.
3. Со свободно-конструируемым ответом. Задания такого типа являются наиболее предпочтительными для автоматизированного обучения и контроля. Они позволяют слушателю общаться с компьютером на естественном языке, имитируя диалог обучаемого и преподавателя. Задания со свободно-конструируемым ответом наиболее сложны для обучаемого, так как полностью исключают возможность угадывания и требуют значительной умственной работы перед вводом в компьютер ответа, набираемого на клавиатуре в свободной форме. В то же время резко возрастает сложность деятельности преподавателя - автора курса по формированию автономных ответов для анализатора инструментальной системы.
Эталон может содержать, как правило, не более 80 символов, включая пробелы. Ответ обучаемого на заданный вопрос сравнивается с текстом эталона и вырабатывается соответствующий признак ответа: «верный», «неверный», «предполагаемый» и т.д. Далее программа переходит к тому кадру сценария, который соответствует полученному признаку.
Таким образом, автор курса формирует кадры, предъявляемые обучаемому в зависимости от признака ответа, что создает иллюзию «понимания» системой смысла введенной фразы, так как при разных ответах на один и тот же вопрос обучаемый получает и различную реакцию компьютера.
В современных инструментальных системах реализованы следующие методы сравнения эталонного ответа с ответом обучаемого.
1. Анализ по ключевым словам. Этот метод анализа достаточно прост и универсален. Эталонный ответ, заранее введенный преподавателем, используется в качестве ключа, который сравнивается с ответом обучаемого на протяжении всей строки. Ключом может быть один символ, слово или группа слов.
При использовании ключевых слов можно достичь достаточно хороших результатов. Но применять метод надо достаточно осторожно, так как возможности распознавания смысла с его помощью ограничены. Недостаток ключевого поиска выражается в том, что ответ не распознается при перестановках внутри ключа.
2. Синтаксический анализ с использованием символов частичной обработки ответа обучаемого. Этот метод анализа целесообразно использовать в том случае, когда требуется выполнить сравнение не по ключу, а по жесткому эталону. Лишний символ должен считаться ошибкой, пробелы не игнорируются. Выполняется как бы прямое (посимвольное) сравнение посимвольного ответа с эталоном. При совпадении всех символов ответа с символами эталона вырабатывается признак «верно».
Однако при работе обучаемых с курсом могут возникнуть ситуации, когда необходимо, с целью более корректного толкования смысла ответа, сделать некоторые отступления от правил прямого сравнения. В подобных ситуациях метод синтаксического анализа предусматривает средства частичной обработки ответов обучаемого.
Символы частичной обработки ответа (спецсимволы), включенные в эталон ответа, позволяют исключить, игнорировать в ответе обучаемого один или несколько символов (слов) при сравнении с эталоном. Все остальные символы, отличные от символов частичной обработки, в тексте обучаемого должны следовать в том же порядке, что и в эталоне ответа.
3. Логический анализ. Логический метод анализа дает возможность формирования ответа в свободно-конструируемой форме. В данном случае ответ может представлять собой фразу или предложение, в котором порядок слов строго не определен. В словах могут игнорироваться окончание или другие части.
Основным отличием данного метода анализа от анализа по ключевым словам является то, что исключается необходимость перечисления всех возможных последовательностей ключевых слов при рассмотрении многословных ответов, так как логический метод позволяет с помощью одного эталона проанализировать насколько вариантов ответов.
Цель этой деятельности - преодоление чрезмерной заданностн ответов обучаемого, что является общим недостатком многих ППС.
Недостатками такого рода программ являются
• снижение мотивации в ходе работы с программой;
• возникновение «провалов» (пробелов) в знаниях, связанных с непроизвольным рассеянием внимания в процессе работы с программой, а также ослаблением системного связывания знаний при отсутствии их интонационного выделения;
• сложность и высокая трудоемкость организации учебного диалога, а также диагностирующей и управляющей обучением части программы.
Ввиду чрезвычайно высокой трудоемкости написания программ такого рода на языках программирования и высоких требований к программистской квалификации разработчиков, они часто разрабатываются с использованием программных оболочек автоматизированных учебных курсов, имеющих свой язык программирования, интерфейс, рассчитанный на разработчика-непрограммиста.
Существует и продолжает разрабатываться большое количество инструментальных программ такого вида. Общим их недостатком является высокая трудоемкость разработки, затруднения организационного и методического характера при использовании в реальном учебном процессе школы. Организационные трудности связаны с тем, что такие программы невозможно использовать в структуре урока из-за больших различий в темпе обучения разных учащихся. Методические трудности проявляются в том, что многие педагоги нередко склонны не соглашаться с методическими решениями и ходами при изложении теоретического материала, предложенными разработчиками инструментальной программы. В работе хорошего учителя много творческих, авторских моментов, в важности которых часто не отдают себе отчета создатели программ.
Программы 3-го типа
(моделирующие) основаны на графически-иллюстративных возможностях компьютера, с одной стороны, и вычислительных, с другой, и позволяют осуществлять компьютерный эксперимент. Такие программы предоставляют ученику возможность наблюдать на экране дисплея некоторый процесс, влияя на его ход подачей команды с клавиатуры, меняющей значения параметров.
Программы 4-го типа
(игры) предоставляют в распоряжение ученика некоторую воображаемую среду, существующий только в компьютере мир, набор каких-то возможностей и средств их реализации. Использование предоставляемых программой средств для реализации возможностей, связанных с изучением мира игры и деятельностью в этом мире. приводит к развитию обучаемого, формированию у него познавательных навыков, самостоятельному открытию им закономерностей, отношений объектов действительности, имеющих всеобщее значение.
Наибольшее распространение получили обучающие программы первых двух типов в связи с их относительно невысокой сложностью, возможностью унификации при разработке млогих блоков программ. Если программы 3-го и 4-го типов требуют .большой работы программистов, психологов, специалистов в области изучаемого предмета, педагогов-методистов, то технология создания программ 1-го и 2-го типов ныне сильно опростилась с появлением инструментальных средств или наполняемых автоматизированных обучающих систем (АОС).
Основные действия, выполняемые программами первых двух типов:
• предъявление кадра с текстом и графическим изображением;
• предъявление вопроса и меню вариантов ответа (или ожидание ввода открытого ответа);
• анализ и оценка ответа;
• предоставление кадра помощи при нажатии специальной клавиши. Они могут быть легко и унифицированно запрограммированы, так что разработчику обучающей программы остается ввести в компьютер только соответствующий текст, варианты ответов, нарисовать на экране с помощью манипулятора «мышь» картинки. Создание обучающей программы в этом случае выполняется совершенно без программирования, не требует серьезных компьютерных познаний и по силам любому педагогу-предметнику средней школы. Названия наиболее известных отечественных АОС: «Урок», «Адонис», «Магистр», «Stratum». Используются в России и зарубежные системы: «Linkway», «TeachCad» и др. Многие из этих систем имеют хорошие графические подсистемы и позволяют создавать не только статические картинки, но и динамические графические фрагменты в духе «мультимедиа» (речь об этом пойдет ниже).
Создание обучающей системы с использованием инструментальных программ обычно проходит четыре стадии.
1. Разработка сценария обучающей программы: на этой стадии педагог должен принять решение о том, какой раздел какого учебного курса он будет переводить в обучающую программу, продумать материал информационных кадров, такие вопросы и варианты ответов к ним, чтобы они диагностировали трудности, с которыми будут сталкиваться ученики при освоении материала, разработать схему прохождения программы, систему взаимосвязей между ее отдельными кадрами и фрагментами.
2. Ввод в компьютер текстов отдельных кадров будущей программы, рисование картинок, формирование контролирующих фрагментов: вопросов, вариантов ответов к ним и способов анализа правильности ответов. На этой стадии педагогу потребуется минимальное владение функциями компьютера и возможностями ввода и редактирования, встроенными в инструментальную программу.
3. Связывание отдельных элементов обучающей программы в целостную диалоговую систему, установление взаимосвязей между кадрами, вопросами и помощью, окончательная доводка программы.
4. Сопровождение программы во время ее эксплуатации, внесение в нее исправлений и дополнений, необходимость которых обнаруживается при ее использовании в реальном процессе обучения.
Очевидно, что создание обучающих программ средствами инструментальных систем поможет снять остроту главной проблемы компьютерного обучения -отсутствия в достаточном количестве и разнообразии качественных обучающих программ, так чтобы компьютерное обучение могло превратиться из жанра «показательных выступлений» на открытых уроках в действительно систематическое обучение учебным дисциплинам или их большим разделам.
В качестве первого шага к компьютерным технологиям обучения нужно рассматривать тренирующие и контролирующие программы. Нет ничего проще (с этой задачей могут справиться даже учащиеся старших классов, изучающие информатику), чем подготовить контролирующую программу по любому разделу любого учебного курса на языке программирования BASIC или с использованием инструментальных программ.
Использовать такие контролирующие программы можно систематически. Это не потребует кардинальных изменений в существующем учебном процессе и избавит учителя от непроизводительных, рутинных операций по проверке письменных работ, контролю знаний учащихся, решит проблему накопляемости оценок. Из-за тотальности контроля учащиеся получат мощный стимул к обучению.
Следующая проблема компьютерного обучения связана с тем, что использование компьютера не вписывается в стандартную классно-урочную систему. Компьютер - это средство индивидуального обучения в условиях нелимитированного времени, и именно в этом качестве он должен использоваться. Соответствующие организационные формы учебного процесса и труда учителей еще предстоит найти и внедрить в практику. Важно, чтобы ученик при компьютерном обучении не был ограничен жесткими временными рамками, чтобы педагогу не надо было работать «на класс» в целом, а чтобы он мог пообщаться с каждым учеником, дать индивидуальную консультацию по работе с обучающей программой и по материалу, в ней содержащемуся, помочь преодолеть индивидуальные затруднения.
При проведении урока с использованием компьютеров работа педагога проходит фазы
• планирования урока (определяется место урока в системе занятий по данной дисциплине, время проведения в кабинете электронно-вычислительной техники, тип урока и его примерная структура, необходимые для его проведения программные средства);
• подготовки программных средств (наполнение оболочек контролирующих программ и обучающих систем соответствующими дидактическими материалами, подбор моделирующих программ, размещение программных средств на соответствующем магнитном диске, проверка запускаемости программ);
• проведения самого урока;
• подведения итогов (внесение исправлений в обучающие программы, архивирование их для будущего использования, обработка результатов компьютерного тестирования, удаление лишних временных файлов с магнитных дисков).
Отдельное направление использования компьютера в обучении - интегрирование предметных учебных курсов и информатики.
При этом компьютер используется уже не как средство обучения, а как средство обработки информации, получаемой при изучении традиционных дисциплин - математики, физики, химии, экологии, биологии, географии. С помощью инструментальных программ на компьютере можно решать математические задачи в аналитическом виде, строить диаграммы и графики, проводить вычисления в табличном виде, готовить текст, схемы и т.д. Компьютер выступает при этом в качестве средства предметной деятельности, приближая стиль учебной деятельности на уроках к стандартам современной научной, технологической и управленческой деятельности.
Особые ожидания при таком использовании компьютера связываются с компьютерными телекоммуникациями, с возможностями локальных и глобальных компьютерных сетей. Весьма перспективной технологией обучения является метод групповых исследовательских проектов, моделирующий деятельность реального научного сообщества. Такая технология включает следующие моменты:
• первоначальную мотивацию исследования; обнаружение какого-либо парадокса, постановку проблемной задачи;
• поиск объяснения парадокса, построение гипотез;
• проведение исследований, экспериментов, наблюдений и измерений, литературных изысканий с целью доказать или отвергнуть гипотезы, объяснения;
• групповое обсуждение результатов, составление отчета, проведение научной конференции;
• решение вопроса о практическом применении результатов исследований; разработку и защиту итогового проекта по теме.
Работа над проектом продолжается от двух недель до двух месяцев. На заключительных стадиях работы над проектом обычно возникают новые проблемные задачи, обнаруживаются новые парадоксы, т.е. создается мотивация для осуществления новых проектов.
Использование компьютера очень хорошо вписывается в эту технологию обучения, особенно если имеется возможность реализовать компьютерные телекоммуникации: обмениваться сообщениями по электронной почте с классами в других городах и даже странах, параллельно выполняющими такой же проект.
Телекоммуникационная составляющая проекта позволяет резко повысить интерес учащихся к выполнению проекта, делает естественным использование компьютера для представления результатов наблюдений и измерений, способсгвует формированию информационной культуры учащихся. Проекты, построенные на сопоставлении местных условий, изучении в них общего и особенного, прививают учащимся глобальное видение мира. Учебные телекоммуникационные проекты чрезвычайно популярны в Соединенных Штатах. Сотни таких проектов для десятков тысяч классов во всех странах мира проводят ежегодно многие глобальные компьютерные сети учебно-научного назначения. Имеется опыт использования телекоммуникационных проектов и в российских условиях.
Содержание обучения по методу проектов является межпредметным, интегрированным, привлекающим знания из различных областей, как и проблемы, возникающие на практике. Обучение по методу проектов, кроме изучения конкретных разделов наук, позволяет достигать и другие педагогические цели:
• развитие письменной речи;
• овладение компьютерной грамотностью, освоение текстового редактора, компьютерных телекоммуникационных программ;
• развитие общих навыков решения проблем;
• развитие навыков работы в группе;
• развитие навыков творческой работы.
В перспективе - развитие учебных курсов, использующих метод групповых проектов и компьютерные телекоммуникации, по разделам краеведения в географии и истории, по биологии и литературе, по иностранным языкам.
ТРАНСЛЯЦИЯ ПРОГРАММ И СОПУТСТВУЮЩИЕ ПРОЦЕССЫ
С появления первых компьютеров программисты серьезно задумывались над проблемой кодирования компьютерных программ. Уже с конца 40-х годов стали появляться первые примитивные языки программирования высокого уровня. В них программист записывал решаемую задачу в виде математических формул, а затем, используя специальную таблицу, переводил символ за символом, преобразовывал эти формулы в двухлитерные коды. В дальнейшем специальная программа (впоследствии названная интерпретатором) превращала эти коды в двоичный машинный код. Первый компилятор был разработан Г. Хоппер в начале 50-х годов; он осуществлял функцию объединения команд и в ходе трансляции производил организацию подпрограмм, выделение памяти компьютера, преобразование команд высокого уровня (в то время псевдокодов) в машинные команды. В дальнейшем компиляторы и интерпретаторы для языков Ассемблера стали развиваться и прочно вошли в практику компьютерного дела.
Идеи трансляции (перекодирования) одних символов в другие легли в основу создания различных языков программирования с соответствующими трансляторами - компиляторами и/или интерпретаторами. Отличие компиляторов от интерпретаторов заключается в процедуре трансляции текста в машинный код. Компилятор преобразует весь текст программы в последовательный набор машинных команд, который в дальнейшем отправляется на выполнение (пример компилятора с языка Паскаль). Интерпретатор же осуществляет трансляцию по принципу синхронного перевода. Каждая отдельная строка программного текста транслируется, а затем, после ее интерпретации, команды этой строки выполняются (пример языка Бейсик). Современные трансляторы с языков программирования высокого уровня, систем управления базами данных интегрируют в себе возможности и достоинства компиляторов и интерпретаторов, а в системы программирования добавляют различные сервисные утилиты по трансляции и отладке создаваемых программ.
Важнейшим элементом в развитии систем программирования выступили подпрограммы. Появление аппарата подпрограмм существенно облегчило процесс разработки системных и прикладных программ.
Подпрограммы позволили формировать библиотеки из наиболее часто употребляемых в программах алгоритмов -процедур и функций. В системах программирования обязательно присутствуют стандартные (встроенные в систему) библиотеки подпрограмм. Например, в их число входят подпрограммы вычисления математических функций sin(х), cos(x), abs(х) и др.
В настоящее время распространены пользовательские и прикладные библиотеки подпрограмм. Их число увеличивается. Меняется структура библиотечных подпрограмм. В современных языках получили распространение модули (Unit), представляющие специализированные пакеты взаимосвязанных подпрограмм определенного предназначения, например по работе с клавиатурой, с графикой и пр. Развитие объектно-ориентированного программирования позволило создавать библиотеки объектов и подпрограмм с объектными типами данных (Object). Примером могут служить оболочки типа TurboVision.
Современная программа представляет набор команд, операторов и выражений, в которых имеются ссылки (прямые или косвенные) на различные подпрограммы из существующих в системе программирования библиотек, модулей, объектов. В этой связи исходный текст программы, как правило, занимает по объему места в памяти в несколько раз меньше, чем его оттранслированный вариант в машинных кодах. Как это происходит?
Рассмотрим один из вариантов трансляции программы с языка программирования Паскаль. Исходный текст программы решения квадратного уравнения представлен ниже:
program KvadUravn;
var А, В, С, D, XI, Х2: REAL;
begin
writeln;
writeln( 'введи
А,В,С') ; read(A,B,C);
D:=B*B-4*A*C;
if D<0 then write('корней нет')
else begin
X1:=(-B+sqrt(D))/(2*A);
X2:=(-B-sqrt(D))/(2*A);
write('X1=', X1,' X2=', Х2);
end
end.
Предположив, что этот текст (по отношению к процессу трансляции выступающий как исходный
модуль) сформирован одним из текстовых редакторов, попытаемся отправить его на выполнение. Прежде всего его необходимо перевести в машинный двоичный код (называемый абсолютным или загрузочным модулем).
Для этого на первых этапах осуществляется трансляция (в данном случае, как это реализовано в системах программирования Паскаля, компиляция) исходного текста в машинный код (объектный модуль). Однако, объектный модуль не может быть использован для выполнения программы, поскольку в нем нет программ по выполнению процедур ввода (read) и вывода (write, writeln), а также вычисления функции извлечения квадратного корня (sqrt). В исходном тексте программы ссылки на указанные библиотечные подпрограммы отмечены знаком {*}.
Следующий шаг трансляции - компоновка - заключается в подключении к исходному объектному модулю объектных модулей соответствующих подпрограмм в места ссылок на них (исходные тексты этих подпрограмм в системе вовсе отсутствуют). Другими словами, на место процедуры Write помещается подпрограмма, осуществляющая процедуру вывода данных на экран дисплея. Таким образом после компоновки (или, иначе, редактирования связей link editor) возникает абсолютный модуль, намного превышающий по объему размер исходного текста программы, Он и является исполняемым компьютером после его запуска. Расширениями его файлового имени, как правило, являются .com или .ехе.
В силу того, что объектные модули не предназначены для непосредственного исполнения, в них обычно нет привязки составляющих их машинных команд к конкретному месту в ОЗУ. Адреса машинных слов бывают условными, что помогает компоновщику размещать объектные модули в свободных местах ОЗУ (заменяя условные адреса команд на конкретные).
Многие системы программирования дополнительно содержат промежуточные этапы трансляции. В этих системах на первом шаге предусмотрена трансляция исходного текста в макроассемблерный код, а затем в объектный модуль. Это связано с историей развития языков программирования, а также с тем, что многие подпрограммы удобнее писать на языке Ассемблера, и подключать их легче на этапе линко-вания ассемблерного модуля с ассемблерными библиотеками подпрограмм.
В современных системах программирования, например, Турбо-Паскаль, Турбо-Си весь этот сложный процесс трансляции с компоновкой подпрограмм скрыт от пользователя и осуществляется специальными компиляторами.
Коротко об отладчиках. Эти программы входят в современные системы программирования и предоставляют средства для просмотра и изменения значений переменных в ходе отладки программы, поиска ошибок и т.д. Использование отладчиков значительно облегчает процесс доводки больших программ.
Заметим, что описанный процесс трансляции характерен для компиляции. Последовательно реализованный интерпретатор объектного модуля фактически не создает. В этом его и недостаток, и достоинство (экономия машинной памяти). Впрочем, у современных ЭВМ, в том числе и персональных, проблема малого ОЗУ отходит на второй план, и интерпретация встречается все реже, так как эффективность этого процесса в целом значительно ниже.
Остается непонятным, как детально происходит трансляция. Пользователь может не уметь сам вручную оттранслировать программу (даже столь короткую, как вышеприведенная), но элементарное понимание этого сложного процесса необходимо.
На первом этапе транслятор производит синтаксический анализ исходной программы - проверяет, не нарушены ли формальные правила, содержащиеся в данном языке программирования. Например, в Паскале текст
может встретиться либо внутри текстовой константы (т.е. в апострофах), либо внутри комментария. Если такой текст встретился в другом месте, то это явная ошибка. В системе программирования встроены описания всех синтаксически разрешенных конструкций, и транслятор их применяет к исходной программе. Для задания синтаксиса применяются формы Бэкуса-Наура и синтаксические диаграммы, о которых будет рассказано в следующей главе.
Первой фазой синтаксического анализа является лексический анализ. Он заключается в просмотре литер исходной программы и построении из них лексически допустимых единиц - идентификаторов, ключевых слов языка, чисел и т.д. Во второй фазе эти единицы уже рассматриваются как неделимые и проверяется допустимость их сочетания.
Даже если в синтаксическом смысле исходная программа верна, это не означает, что она имеет смысл в рамках данного языка программирования.На следующем этапе семантического анализа транслятор ищет ошибки такого рода: числа употребления слов BEGIN и END не совпадают; переменные не описаны (в языке, требующем обязательного явного описания переменных), т.е. текст программы непонятен (семантика - смысловая сторона языка).
Лишь после того, как в программе все синтаксически правильно и семантически понятно, транслятор переводит операторы программы в машинный код. Это отнюдь не означает, что в программе все благополучно - не исключены ошибки этапа исполнения (деление на ноль, выход за границу массива, переполнение разрядов и т.д.).
Различные фазы компиляции могут быть как последовательными, так и частично перекрывающимися во времени. В зависимости от способа реализации компилятор читает и обрабатывает исходный текст один или несколько раз, называясь соответственно однопроходным, двухпроходным и т.д.
ТУРБО-ОБОЛОЧКИ. ВЕРСИИ ПАСКАЛЯ
Система программирования Турбо-Паскаль 3.0. После запуска программы turbo.exe на экране появится меню системы
| Logged drive : A
Work fi1е: Main file: Edit Compile Run Save eXecute Dir Quit compiler Options Text: 0 bytes (7BF5-7BF5) Free: 19472 by tes (7BF6-C806) > |
Рис. 3.2. Главное меню Турбо-Паскаля 3.0
Соответствующие команды выполняются при нажатии выделенной большой буквы.
Logged drive: команда «L» осуществляет выбор дисковода: на запрос
(выбор устройства) NEW DRIVE ввести одну из букв от А до Р, oбозначающую номер дисковода;
Work file: команда «W» осуществляет выбор рабочего файла, на
(рабочий файл) запрос Work file name ввести имя вашего файла;
Main file: команда «М» выбирает основной файл для программ,
(основной файл) использующих директивы $I: аналогична команде «W»;
Edit команда «Е» вызывает текстовый редактор; если не
(редактор) выбран файл, то будет запрос; инструкцию по работе с редактором см. ниже;
Compile команда «С» осуществляет компиляцию программы,
(компиляция) компиляция проводится в память, режим компиляции (в СОМ или CHN файлы) меняют по команде «О» (см. compiler Options );
Run команда «R» запускает откомпилированную или
(запуск) неоткомпилированную программу;
Save команда «S» осуществляет запись рабочего (сохранить)
(сохранить) файла с сохранением предыдущей версии с расширением .ВАК;
EXecute команда «X» осуществляет вызов и выполнение любого
(выполнять) СОМ-файла;
Dir команда «D» осуществляет просмотр директории
(оглавление файлов);
Quit команда «Q» осуществляет выход из системы; если файл
(прервать) не записан, то будет запрос;
compiler Options команда «О» выбирает режим компиляции
(опции компилятора) с помощью меню

(команды «М», «С» и «Н» осуществляют выбор режима компиляции в память, в corn-файл и в chn-файл (откомпилированный файл без библиотеки),
команда «Q» возвращает в основное меню)
Описание языка Паскаль, проведенное в §3, соответствует версии 3. Исключение составляет раздел работы с графикой, в котором использован универсальный модуль Graph для версий 5 и выше. Таким образом, практически все приведенные в главе примеры могут быть реализованы в среде Турбо-Паскаль 3 (и, разумеется, в более поздних версиях)
Система программирования Турбо-Паскаль 5.5. Ниже перечисляются основные расширения возможностей версии Турбо-Паскаля 5.5:
•допускается изменение структуры Паскаль-программы, заголовок программы (program) не обязателен, разделы глобальных описаний могут следовать в любом порядке;
• расширен синтаксис описания констант, разрешено определять типизированные константы и производить их инициализацию;
• введены шестнадцатиричные константы;
• расширен список арифметических функций;
• введены типы данных Word, Byte,
• значительно расширен список процедур и функций для работы с файлами и модулями.
Начиная с версии 4.0 в Турбо-Паскале введено понятие модуля (Unit), определены его составляющие части, а также разрешена раздельная компиляция модулей.
Имеются стандартные модули Crt, Svstem, dos, Graph, Turbo3. Graph3. Последние модули призваны осуществлять совместимость с предыдущими версиями.
В системе программирования Турбо-Паскаль версии 5.5 создана интегрированная среда разработчика, т е ряд специализированных средств и возможностей, объединенных оконным турбо-меню (контекстное меню). Главное меню интегрированной среды содержит следующие пункты:
File Edit Run Compile Options Debug Break/watch
Система вступает в диалог с пользователем и предоставляет возможность обратиться к контекстной помощи в любой момент.
Как правило, работа в среде начинается с загрузки текста программы или с его формирования в окне редактирования. После редактирования программы осуществляется компиляция и выполнение, которые выполняются при нажатии клавиш Ctrl+F9 (эквивалентно выбору команды run из меню Run).
Во время компиляции программы на экране появляется специальное окно, в котором информируется процесс компиляции. В случае обнаружения ошибки компиляция прерывается и активизируется встроенный редактор, в котором курсор указывает место ошибки. Клавиша F1 в этот момент выводит информацию из службы помощи по диагностике ошибки. Исправив ошибку, можно опять отправить программу на компиляцию. После удачной компиляции программа выполняется и результаты ее работы можно просмотреть нажатием клавиш Alt+F5. В процессе компиляции выявляются лишь синтаксические ошибки. Правильность работы программы необходимо проверять специальными приемами. В интегрированной среде разработчика предусмотрен отладчик, позволяющий осуществлять трассировку программы или ее отдельных участков, прерывать выполнение в заданных точках, следить за изменениями значений различных переменных. Трассировкой называют пошаговое исполнение программы, при котором за один шаг выполняются все операторы одной строки с последующим ожиданием. Очевидно, что трассировка эффективнее работает для исходного текста, в котором в строке помещают не более одного оператора.
При этом появляется возможность анализировать результаты работы каждого оператора в отдельности.
Сеанс отладки обычно начинается с команды Trace into (F*) или Step over (F8) из меню Run. Выборочная трассировка отдельных участков исходного текста осуществляется с помощью команд Toggle breakpoint из меню Break/Watch и Go to cursor меню Run, Для наблюдения за значениями переменных и выражений существует окно просмотра Watch (F6) в меню Debug. В нем отображаются текущие значения выбранного выражения. Сеанс отладки программы необходимо завершать командой Program reset (Ctrl+F2) из меню Run.
Система программирования Турбо-Паскаль 6.0. Главное меню интегрированной среды содержит следующие пункты. Е - системное меню;
File - работа с файлами (сохранение, загрузка, связь с операционной системой);
Edit -редактирование текущего файла (стандартные возможности встроенного текстового редактора);
Search - поиск и замена фрагментов текста;
Run -запуск программы на выполнение;
Compile -компиляция программы:
Options - установка опций интегрированной среды;
Debug - установка параметров отладки программы;
Window - работа с окнами;
Help - система помощи и подсказок.
Версия 6.0 является развитием и усовершенствованием версии 5.5. Существенно переработана интегрированная среда пользователя. В ней появилась возможность работать в многооконном режиме, редактируя несколько файлов одновременно. Допускается работа с «мышью». Существенно улучшен сервис для работы с окнами и с системой помощи Help, которая контекстно вызывается из любого окна, а в окне Help допустимы некоторые команды редактирования. Увеличился максимальный размер редактируемого файла и имеется возможность менять цветовую палитру самой интегрированной среды.
Еще одна возможность, появившаяся в Турбо-Паскале 6.0 - объектно-ориентированное проектирование программ. Подобная технология стала возможной благодаря новому типу данных «объект».
Объект - это структура данных, содержащая поля данных (подобно записи) различных типов и заголовки методов. Метод - это процедура или функция, объявленные внутри объявления элемента типа «объект». Большую популярность среди программистов приобрела объектно-ориентированная библиотека TurboVision, включающая объекты, управляющие
• перекрывающими окнами с изменяемыми размерами;
• выпадающими меню;
• диалоговыми окнами;
• работой мыши;
• кнопками,полосами скроллинга.
Следует отметить, что сама интегрированная среда Турбо-Паскаля 6.0 разработана с использованием библиотеки TurboVision.
Система программирования Турбо-Паскаль 7.0. Главное меню интегрированной среды Турбо-Паскаль 7.0 в дополнение к меню Турбо-Паскаля 6.0 содержит
Tools - инструментальные программные средства.
По сравнению с предыдущей версией в интегрированной среде появилась возможность настройки компилятора на работу в трех режимах: обычном режиме MS DOS (Real), защищенном режиме (Protected) и в режиме операционной среды Windows (Windows). Введена новая команда Object Browser - просмотр модулей, объектов и символов при редактировании исходного текста. Появилось удобное средство - синтаксическая подсветка, которая обеспечивает подсвечивание управляющих структур, зарезервированных слов, идентификаторов, строк и т.п. Новая секция меню Tools предназначена для передачи управления внешним программам и создания собственных инструментальных программных средств. Нажатие клавиш Alt+Fl (или правый щелчок мыши) активизирует локальные меню, чувствительные к контексту (Browse, Edit, Help, Message, Watch).
В версии 7.0 расширена библиотека стандартных модулей. Помимо известных в версии 6.0 модулей Crt, Graph, Graph3, Overlay, String, System, Turbo3 появились WinAPI, WinCrt, WinDos, WinPrn, WinTypes, WinProcs.
§ УЧЕБНАЯ МОДЕЛЬ МИКРОКОМПЬЮТЕРА
В предыдущем разделе были кратко изложены наиболее важные черты реально существующего простого процессора ЭВМ. Конечно, на самом деле все устроено заметно сложнее, поэтому мы ограничились достаточно поверхностным знакомством. Более современные процессоры устроены еще сложнее.
Существует альтернативный подход - изучение сложного объекта на упрощенной модели, сохраняющей все его наиболее существенные черты. Именно такой подход использован в данном разделе. Рассмотрение фундаментального материала, освобожденного от второстепенных технических деталей, помимо простоты имеет и еще одно преимущество - полученные знания не так быстро «стареют».
Прием, состоящий в объяснении принципов работы ЭВМ на базе учебной модели, возник довольно давно. Имеется целый ряд учебных моделей: «Кроха», «Нейман», «Малютка» и другие (описание которых можно найти в рекомендуемой в конце главы дополнительной литературе).
В данном параграфе рассматривается учебная модель микропроцессорной ЭВМ четвертого поколения, предложенная преподавателем Пермского педагогического университета Е.А.Ереминым. Модель носит название «Е97» В нее включены наиболее характерные черты устройства современных компьютеров. Модель не повторяет полностью ни один реальный компьютер, хотя дает достаточно полное представление об его устройстве. В «Е97» нет излишних технических деталей, он достаточно прост и содержит только то, что необходимо для изучения.
«Е97» может работать как с числовыми, так и с нечисловыми данными, отражает общепринятую байтовою организацию памяти, способен обрабатывать массивы информации (поскольку имеет современные методы адресации), реалистически отражает работу с периферийными устройствами современного компьютера. Существенно, что наряду с теоретической моделью компьютера создана программа-эмулятор, позволяющая имитировать «Е97» на различных компьютерах, в том числе IBM-совместимых. Ряд непринципиальных ограничений и нереализованных возможностей, указанных ниже, относятся именно к этой программе-эмулятору.
УПРАВЛЯЕМЫЕ СИСТЕМЫ
Несмотря на такое многообразие задач, решаемых в разных разделах кибернетики, разнообразие моделей, подходов и методов, кибернетика остается единой наукой благодаря использованию общей методологии, основанной на теории систем и системном анализе.
Система - это предельно широкое, начальное, не определяемое строго понятие. Предполагается, что система обладает структурой, т.е. состоит из относительно обособленных частей (элементов), находящихся, тем не менее, в существенной взаимосвязи и взаимодействии. Существенность взаимодействия состоит в том, что благодаря ему элементы системы приобретают все вместе некую новую функцию, новое свойство, которыми не обладает ни один из элементов в отдельности. В этом состоит отличие системы от сети, также состоящей из отдельных элементов, но не связанных между собой существенными отношениями. Сравните, например, предприятие, цеха которого образуют систему, поскольку лишь все вместе приобретают свойство выпускать конечную продукцию (и ни один из них в отдельности с этой задачей не справится), и сеть магазинов, которые могут работать независимо друг от друга.
Кибернетика как наука об управлении изучает не все системы вообще, а только управляемые системы. Зато область интересов и приложений кибернетики распространяется на самые разнообразные биологические, экономические, социальные системы.
Одной из характерных особенностей управляемой системы является возможность переходить в различные состояния под влиянием различных управляющих воздействий. Всегда существует некое множество состояний системы, из которых производится выбор предпочтительного состояния.
Отвлекаясь от конкретных особенностей отдельных кибернетических систем и выделяя общие для некоторого множества систем закономерности, описывающие изменение их состояния при различных управляющих воздействиях, мы приходим к понятию абстрактной кибернетической системы. Ее составляющими являются не конкретные предметы, а абстрактные элементы, характеризующиеся определенными свойствами, общими для широкого класса объектов.
Поскольку под кибернетическими системами понимаются управляемые системы, в них должен присутствовать механизм, осуществляющий функции управления. Чаще всего этот механизм реализуется в виде органов, специально предназначенных для управления, рис. 1.44.

Рис. 1.44. Схематическое изображение кибернетической системы
в виде совокупности управляющей (А) и управляемой (В) частей
Стрелками на рисунке обозначены воздействия, которыми обмениваются части системы. Стрелка, идущая от управляющей части системы к управляемой, обозначает сигналы управления. Управляющая часть системы, вырабатывающая сигналы управления, называется управляющим устройством. Управляющее устройство может вырабатывать сигналы управления, обычно на основе информации о состоянии управляемой системы (изображены на рисунке стрелкой от управляемой части системы к управляющей ее части), о требуемом ее состоянии, о возмущающих воздействиях. Совокупность правил, по которым информация, поступающая в управляющее устройство, перерабатывается в сигналы управления, называется алгоритмом управления.
На основе введенных понятий можно определить понятие «управление». Управление - это воздействие на объект, выбранное из множества возможных воздействий на основе имеющейся для этого информации, улучшающее функционирование или развитие данного объекта.
В системах управления решаются четыре основных типа задач управления: 1) регулирование (стабилизация), 2) выполнение программы, 3) слежение и 4) оптимизация.
Задачами регулирования являются задачи поддержания параметров системы -управляемых величин - вблизи некоторых неизменных заданных значений {х} несмотря на действие возмущений М, влияющих на значения {х}. Здесь имеется в виду активная защита от возмущений, принципиально отличающаяся от пассивного способа защиты. Пассивная защита
заключается в придании объекту таких свойств, чтобы зависимость интересующих нас параметров от внешних возмущений была мала. Примером пассивной защиты является теплоизоляция для поддержания заданной температуры системы, антикоррозионные покрытия деталей машин. Активная защита предполагает выработку в управляющих системах управляющих воздействий, противодействующих возмущениям.
Так, задача поддержания необходимой температуры системы может быть решена с помощью управляемого подогрева или охлаждения.
Задача выполнения программы возникает в случаях, когда заданные значения управляемых величин {х}
изменяются во времени известным образом, например, в производстве при выполнении работ согласно заранее намеченному графику. В биологических системах примерами выполнения программы являются развитие организмов из яйцеклеток, сезонные перелеты птиц, метаморфозы насекомых.
Задача слежения - поддержание как можно более точного соответствия некоторого управляемого параметра X0(t) текущему состоянию системы, меняющемуся непредвидимым образом. Необходимость в слежении возникает, например, при управлении производством товаров в условиях изменения спроса.
Задачи оптимизации - установления наилучшего в определенном смысле режима работы или состояния управляемого объекта - встречаются весьма часто. Примерами являются: управление технологическими процессами с целью минимизации потерь сырья и т.д.
Системы, в которых для формирования управляющих воздействий не используется информация о значениях, которые управляемые величины принимают в процессе управления, называются
разомкнутыми системами управления. Структура такой системы показана на рис. 1.45.
Рис. 1.45. Алгоритм управления, реализуемый управляющим устройством УУ, которое обеспечивает слежение за возмущением М и компенсацию этого возмущения, без использования управляемой величины Х
Напротив, в замкнутых системах управления для формирования управляющих воздействий используется информация о значении управляемых величин. Структура такой системы показана на рис. 1.46.
Обратная связь
является одним из важнейших понятий кибернетики, помогающим понять многие явления, которые происходят в управляемых системах различной природы. Обратную связь можно обнаружить при изучении процессов, протекающих в живых организмах, экономических структурах, системах автоматического регулирования. Обратная связь, увеличивающая влияние входного воздействия на управляемые параметры системы, называется положительной, уменьшающая влияние входного воздействия - отрицательной.
Рис. 1.46. Связь между выходными параметрами А" и входными У одного и того же элемента управляемой системы называется обратной связью
Положительная обратная связь
используется во многих технических устройствах для усиления, увеличения значений входных воздействий. Отрицательная обратная связь используется для восстановления равновесия, нарушенного внешним воздействием на систему.
УСТРОЙСТВА ВВОДА ИНФОРМАЦИИ
Разумеется, для ввода (и вывода) информации используются все виды ВЗУ. Заметим, что информация в ВЗУ хранится в виде, недоступном для непосредственного восприятия человеком, ибо ВЗУ предназначены для промежуточного хранения данных.
Многие другие устройства ввода/вывода, напротив, предназначены для обмена информацией с человеком.
Важнейшим из устройств ввода, несомненно, является клавиатура. Подавляющее большинство современных клавиатур являются полноходовыми контактными, т.е. клавиша утапливается при нажатии и замыкает контакт между двумя металлическими пластинками, покрытыми, во избежание окисления, пленкой благородного металла. Хорошая клавиатура рассчитана на несколько десятков миллионов нажатий каждой клавиши. При нажатии клавиши генерируется связанный с ней код, заносимый в соответствующий буфер памяти, а при ее отпускании - другой код, что позволяет перепрограммировать назначение клавиш, вводя новую таблицу соответствия этих кодов.
Ряд клавиш при совместном нажатии пары из них генерируют специальный код, отличный от того, который генерируется при нажатии каждой клавиши в отдельности. Это позволяет значительно увеличить возможности клавиатуры. Вспомним, что для передачи всех возможностей при байтовой системе кодирования могло бы понадобиться 256 клавиш, чего нет ни на одной клавиатуре благодаря указанным совмещениям.
Большинство клавиатур имеют стандартные группы клавиш:
• клавиши пишущей машинки - для ввода букв, цифр и других знаков;
• служебные клавиши, перенацеливающие действия остальных (переключатели регистров, переходы с латинского шрифта на русский и другие);
•функциональные клавиши Ft - F12 (иногда их меньше), назначение которых задает разработчик прикладной программы;
• дополнительные цифровые клавиши для большего удобства в работе.
Важным свойством клавиатуры, благодаря которому пользователь может работать не один час подряд, является эргономичность. Этим термином задается совокупность характеристик, определяющих удобство (в широком смысле слова) устройства.
По отношению к клавиатуре это дизайн, отсутствие бликов, удобное взаиморасположение и размеры клавиш и многое другое.
В состав стандартного оснащения современного персонального компьютера входит мышь - устройство ввода и управления. Конструктивно это коробочка с выступающим внизу шариком, который, поворачиваясь, вращает взаимно перпендикулярные колесики. Благодаря наличию в них специальных прорезей оптическая система мыши способна отслеживать и преобразовывать движение шарика в перемещение курсора на экране компьютера. Две или три клавиши на верхней стороне мыши позволяют отдавать многочисленные команды, определяемые текущей программой. То же делает «перевернутая мышь» - шар (trackball), который монтируется в корпус компьютера или клавиатуры.
Есть еще ряд манипуляторов, служащих для ввода информации: световое перо, джойстик и т.д. Они второстепенны, решают некоторые ограниченные задачи.
Все чаще рядом с компьютером оказывается сканер - устройство для ввода с листа бумаги документов (текстов, чертежей и т.д.). Лучик света с огромной скоростью пробегает по листу, светочувствительными датчиками воспринимается яркость (а иногда и цветность) отраженного света и трансформируется в двоичный код. Сканеры бывают цветными и монохромными, с разной разрешающей способностью, разным размером обрабатываемых изображений, настольными и ручными. Наиболее совершенные из них весьма дороги.
Несколько слов о вводе текстов с помощью сканера. Всякую информацию сканер воспринимает как графическую. Если это текст, то чтобы компьютер осознал его в таком качестве и позволил далее обрабатывать как текст (например, программами типа «редактор текстов»), нужна специальная программа распознавания, позволяющая выделить в считанном изображении отдельные символы и сопоставить им соответствующие коды символов. Это - достаточно сложная задача, но она успешно решается.
Не так давно появились средства речевого ввода, которые позволяют пользователю вместо клавиатуры, мыши и других устройств использовать речевые команды (или проговаривать текст, который должен быть занесен в память в виде текстового файла).Возможности таких устройств достаточно ограничены, хотя они постоянно совершенствуются. Проблема не в том, чтобы записать речь, подвергнуть ее дискретизации и ввести коды в компьютер (при современном уровне техники это несложно), а чтобы распознать смысл речи и представить ее, например, в текстовой форме, допускающей последующую компьютерную обработку. Например, программа «Kurzweil Voice 1.0 for Windows» обеспечивает распознавание (на английском языке) всех речевых команд для навигации в среде «Windows», а в режиме диктовки текста способна распознать до 40 тысяч слов, произносимых в среднем для человека темпе речи (требуя, однако, не менее 16 Мбайт ОЗУ и не менее 50 Мбайт на винчестере лишь для самой себя). Многие специалисты связывают с прогрессом устройств речевого ввода будущее компьютерной техники, считая такие устройства ведущими элементами ее интеллектуализации.
УСТРОЙСТВА ВЫВОДА ИНФОРМАЦИИ
Самым популярным из устройств вывода информации является дисплей - устройство визуального отображения текстовой и графической информации. Дисплей относится к числу неотъемлемых принадлежностей компьютера. Есть и параллельные термины, обозначающие почти то же самое: «видеотерминал», «видеомонитор» (хотя есть и смысловые оттенки: «монитор» - устройство управления чем-то, «терминал» - удаленное устройство доступа).
Дисплеи классифицируются по нескольким разным параметрам, отражающим их назначение в конкретной компьютерной системе и возможности. Бывают дисплеи монохромные и цветные. Монохромный дисплей производит отображение в двух цветах - черном и белом, либо зеленом и черном и т.д. Высококачественный цветной дисплей может воспроизводить десятки основных цветов и сотни оттенков.
Бывают дисплеи графические и алфавитно-цифровые (впрочем, последние, способные отображать лишь ограниченный набор основных символов используемого алфавита, почти исчезли из обычного обихода). Графический дисплей может отображать как символы, так и любое изображение, которое можно построить из отдельных точек в пределах разрешающей способности.
По физическим принципам, лежащим в основе конструкций дисплеев, подавляющее большинство их относится к дисплеям на базе электронно-лучевых трубок и к жидкокристаллическим дисплеям (последние особенно часто встречаются у портативных компьютеров). У первых формирование изображения производится на внутренней поверхности экрана, покрытого слоем люминофора - вещества, светящегося под воздействием электронного луча, генерируемого специальной «электронной пушкой» и управляемого системами горизонтальной и вертикальной развертки. Жидкокристаллический экран состоит из крошечных сегментов, заполненных специальным веществом, способным менять отражательную способность под воздействием очень слабого электрического поля, создаваемого электродами, подходящими к каждому сегменту.
При выводе на экран любого изображения, независимо от того, в растровом или векторном форматах оно зафиксировано в графических файлах, в видеопамяти формируется информация растрового типа, содержащая сведения о цвете каждого пиксела, задающего наиболее мелкую деталь изображения.
Каждый пиксел однозначно связан с долей видеопамяти - несколькими битами, в которых программным путем задается яркость (и, при цветном экране, цветность) свечения этого пиксела. Специальная системная программа десятки раз в секунду считывает содержимое видеопамяти и обновляет содержимое каждого пиксела, тем самым создавая и поддерживая на экране изображение. В п. 4.3 говорилось о том, как при этом взаимодействуют процессоры - центральный и контроллер дисплея.
Основные характеристики дисплеев с точки зрения пользователя таковы: разрешающая способность, число воспроизводимых цветов (для цветного дисплея) или оттенков яркости (для монохромного). Для алфавитно-цифрового дисплея разрешающая способность - число строк на экране и символов в каждой строке. Так, дисплей устаревшего отечественного компьютера ДВК-1 (диалоговый вычислительный комплекс) имел разрешающую способность 24х80 символов. Для графического - это число высвечиваемых точек по горизонтали и вертикали. К примеру, в табл. 4.4 приведены характеристики цветного графического дисплея SVGA (Super Video Grapics Adapter - видеографический адаптер повышенного разрешения) в нескольких из возможных режимах работы.
Таблица 4.4
Характеристики SVGA-монитора
|
Режим |
Разрешающая способность |
Число цветов (оттенков яркости) |
|
Символьный |
25х50 |
256 |
|
51х132 |
256 |
|
|
Графический |
768х1024 |
16 |
|
480х640 |
64 |
Огромную роль при выводе информации играют разнообразные печатающие устройства - принтеры.
Наличие дисплея на современных компьютерах позволяет, работая в интерактивном режиме, экономить огромное количество бумаги, но все равно наступает, как правило, момент, когда необходима, так называемая, «твердая копия» информации - текст, данные, рисунок на бумаге. В процессе эволюции принтеры прошли следующий путь. Первые копировали пишущую машинку, имея ударные клавиши с буквами, цифрами и т.д. Под управлением процессора та или иная клавиша наносила удар по красящей ленте, оставляющей след на бумаге. Таких принтеров давно нет; их прямые наследники - точечно-матричные принтеры ударного типа - располагают перемещающейся вдоль строки печатающей головкой, содержащей от 7 до 24 игл, каждая из которых может независимо от остальных наносить удар по ленте. Это позволяет формировать изображения как букв и цифр, так и любых других символов, а также достаточно сложные рисунки и чертежи. Для хранения и подачи ленты используют специальную пластмассовую коробочку -картридж. Принтеры стали «интеллектуальными», т.е. имеют собственное ОЗУ и электронный блок управления для того, чтобы разгрузить основное ОЗУ и не отнимать в процессе печати время у центрального процессора.
Особенность современного принтера - возможность поддержки многих шрифтов. Часть шрифтов «прошита» в памяти принтера и задается нажатием клавиш на его панели, Еще больше шрифтов являются «загружаемыми», т.е. задаются той программой, которая обращается к устройствам печати. К примеру, широко распространенный графический редактор «Лексикон» позволяет пользователю выбирать между «обычным» шрифтом (так называемый шрифт пишущей машинки), жирным, курсивом (т.е. наклонными символами), жирным курсивом, символами с подчеркиванием и другими шрифтами - в зависимости от версии программы. Следует учесть, что при печати «собственными» шрифтами принтер обычно работает быстрее, так как комбинации ударов игл выбираются из знакогенератора принтера; загружаемые шрифты требуют дополнительного времени на загрузку до начала печати соответствующей программы - знакогенератора; самая медленная печать осуществляется в графическом режиме, который требует постоянной пересылки в принтер информации о текущем режиме работы каждой иглы.
Последний (графический) режим с появлением системы «Windows» стал очень распространенным; он не включает предварительной пересылки шрифтов в память принтера.
Приведем названия наиболее распространенных шрифтов, чаще всего «прошитых» в принтерах: roman - шрифт пишущей машинки; bold-face - полужирный; italic - курсив; condenced - сжатый.
Качество печати текста определяется не только шрифтом и классом принтера, но и числом точек, из которых формируется символ. Наиболее быстрый режим с минимально возможным числом точек и весьма невысоким качеством печати -режим черновой печати (draft); наиболее высококачественный - режим SLQ (Super Letter Quality). На одном и том же принтере соотношение скоростей печати в разных режимах может достигать 1:10.
Существуют ударные точечно-матричные принтеры цветной печати. В них используются 4-цветные ленты, и каждая точка изображения формируется четырьмя последовательными ударами иголки разной силы. Таким образом можно сформировать на бумаге точки всех основных цветов и множества оттенков. Крупнейший производитель точечно-матричных принтеров - фирма «Epson» (Япония).
Все чаще на рабочих местах пользователей персональных компьютеров появляются вместо точечно-матричных струйные или лазерные принтеры. Струйные принтеры вместо головки с иглами имеют головку со специальной краской и микросоплом, через которую эта краска «выстреливается» струйкой на бумагу (и быстро сохнет). Для формирования изображения либо струйка краски может отклоняться специально созданным электрическим полем (так как она электризуется в момент выхода из сопла), либо (чаще) головка имеет столбец из нескольких сопел - наподобие матрицы игл точечно-матричного принтера.
Струйные принтеры могут быть цветными, они смешивают на бумаге красители, порознь распыляемые разными соплами. Изображение, формируемое струйными принтерами, по качеству превосходит аналогичное, получаемое на точечно-матричных. Дополнительное достоинство - меньший уровень шума при работе.
Самые высококачественные изображения на бумаге на сегодняшний день дают лазерные принтеры.
Один из основных узлов лазерного принтера - вращающийся барабан, на внешней поверхности которого нанесен специальный светочувствительный материал. Управляемый электронным блоком луч лазера оставляет на поверхности барабана наэлектризованную «картинку», соответствующую формируемому изображению. Затем на барабан наносится специальный мелкодисперсный порошок - тонер, частички которого прилипают к наэлектризованным участкам поверхности. Вслед за этим к барабану прижимается лист бумаги, на который переходит тонер, после чего изображение на бумаге фиксируется («прижигается») в результате прохождения через горячие валки. Все это происходит с огромной быстротой, благодаря чему лазерные принтеры значительно превосходят обсуждавшиеся выше по скорости работы. Лазерные принтеры -рекордсмены по части количества воспроизводимых шрифтов и качеству рисунков благодаря высочайшей разрешающей способности. Существуют как черно-белые, так и цветные лазерные принтеры. Лазерный принтер работает почти бесшумно. Единственный, но, увы, очень важный параметр, по которому они существенно уступают принтерам ранее описанных типов - стоимость; далеко не всякий может себе позволить приобрести принтер, по стоимости превосходящий точечно-матричный аналог в несколько раз.
Лидирующая фирма в производстве струйных и лазерных принтеров - «Hewlett-Packard» (HP), США, хотя в этой области действуют и другие фирмы.
Трудно сравнивать разные принтеры между собой, так как существует множество моделей с очень различающимися характеристиками. Приведем для примера принтеры разных типов примерно одного функционального класса, предназначенные для малого офиса или дома. Девятиигольчатый точечно-матричный EPSON LX 1050 при печати текста имеет максимальную производительность 200 знаков/с (при использовании встроенных шрифтов в режиме draft), т.е. может отпечатать страницу стандартного текста (порядка 30 строк) с очень скромным качеством за 10 с; высококачественная же печать займет до 2 мин. Струйный HP DeskJet 600 печатает со скоростью около 4 стр/мин с разрешением 600 точек/дюйм (весьма высокое качество печати); по скорости он превосходит указанный матричный примерно в 1,5 раза.
Лазерный HP « LaserJet SL» по приведенным характеристикам такой же, как указанный выше струйный, но по стоимости превосходит его примерно вдвое.
Существуют и принтеры, работающие на других физических принципах, но по распространенности они значительно уступают тем, которые обсуждались выше.
К принтерам близки по назначению плоттеры - специализированные устройства для вывода на бумагу чертежей и рисунков. Рисунок исполняется специальным пером, управляемым электронным блоком; для цветного плоттера необходимо несколько перьев. Плоттер необходим как часть АРМа проектировщика, инженера-конструктора, архитектора. В силу специализированности и высокой стоимости плоттеры не являются устройствами массового распространения.
Своеобразные устройства вывода - синтезаторы звука. Простейшие из них есть в арсенале почти у всех персональных компьютеров и представляют собой обычный малогабаритный динамик, напряжение сигнала на котором с большой частотой изменяется компьютером. Таким способом удается подать простой звуковой сигнал, указывающий на наступление какого-либо события. Многие языки программирования дополняются командами типа ВЕЕР, SOUND, позволяющими программировать серии звуков. Если звукогенератор физически реализован так, что частота звучания поддается регулированию, то можно запрограммировать несложную мелодию, а если есть несколько независимых звукогенераторов, то - и звучание оркестра. Для этого в современных компьютерах устанавливается специальная плата - звуковая карта, - способная преобразовывать аналоговый звуковой сигнал в последовательность двоичных цифр и наоборот. Существуют и синтезаторы речи, назначение которых понятно из названия.
ВАЖНЕЙШИЕ НЕВЫЧИСЛИТЕЛЬНЫЕ АЛГОРИТМЫ (ПОИСК И СОРТИРОВКА)
Одними из важнейших процедур обработки структурированной информации являются сортировка и поиск. Сортировкой называют процесс перегруппировки заданной последовательности (кортежа) объектов в некотором определенном порядке. Определенный порядок (например, упорядочение в алфавитном порядке, по возрастанию или убыванию количественных характеристик, по классам, типам и т.п) в последовательности объектов необходим для удобства работы с этими объектами. В частности, одной из целей сортировки является облегчение последующего поиска элементов в отсортированном множестве. Под поиском подразумевается процесс нахождения в заданном множестве объекта, обладающего свойствами или качествами задаваемого априори эталона (или шаблона).
Очевидно, что с отсортированными (упорядоченными) данными работать намного легче, чем с произвольно расположенными. Упорядоченные данные позволяют эффективно их обновлять, исключать, искать нужный элемент и т.п. Достаточно представить, например, словари, справочники, списки кадров в неотсортированном виде и сразу становится ясным, что поиск нужной информации является труднейшим делом, если не невозможным.
Существуют различные алгоритмы сортировки данных. И понятно, что не существует универсального, наилучшего во всех отношениях алгоритма сортировки. Эффективность алгоритма зависит от множества факторов, среди которых можно выделить основные:
• числа сортируемых элементов;
• степени начальной отсортированности (диапазона и распределения значений сортируемых элементов);
• необходимости исключения или добавления элементов;
• доступа к сортируемым элементам (прямого или последовательного).
Принципиальным для выбора метода сортировки является последний фактор. Если данные могут быть расположены в оперативной памяти, то к любому элементу возможен прямой доступ. Удобной структурой данных в этом случае выступает массив сортируемых элементов. Если данные размещены на внешнем носителе, то к ним можно обращаться лишь последовательно. В качестве структуры подобных данных можно взять файловый тип.
В этой связи выделяют сортировку двух классов объектов: массивов (внутреняя сортировка) и файлов (внешняя сортировка).
Процедура сортировки предполагает, что при наличии некоторой упорядочивающей функции F расположение элементов исходного множества меняется таким образом, что
a1, а2… аn > ak1, ak2…akn
F(ak1) < F(ak2) < F(akn)
где знак неравенства понимается в смысле того порядка, который установлен в сортируемом множестве.
Поиск и сортировка являются классическими задачами теории обработки данных, решают эти задачи с помощью множества различных алгоритмов. Рассмотрим наиболее популярные из них.
Поиск. Для определенности примем, что множество, в котором осуществляется поиск, задано как массив
var a:array[0..N] of item;
где item - заданный структурированный тип данных обладающий хотя бы одним полем (ключом), по которому необходимо проводить поиск.
Результатом поиска, как правило, служит элемент массива, равный эталону, или отсутствие такового.
Линейный поиск. Процедура заключается в простом последовательном просмотре всех элементов массива и сравнении их с эталоном X.
i:=0;
while (i<=N)and(a[i]<>X) do i:=i+1 end.
Часто бывает целесообразнее осуществлять поиск с барьером, вводя дополнительно граничный элемент массива a[N+l]:
a[N+l]:=X;i:=0;
while a[i]<>X do i:=i+l end.
Равенство i = N + 1 означает, что совпадений не было, т.е. что эталонный элемент отсутствует.
Попытайтесь разобраться в чем различие представленных конструкций. Приведем пример программы поиска эталона х в массиве а[0..n].
Программа 42
program poiskl; (*линейный поиск*) const
N=8;
type item= integer;
var a : array[0..n] of item; i :integer; x : item;
begin
(*задание
искомого массива*) for i:=0 to N do
begin writet'Bвeди элемент a[ ',i, ']= '); readln(a[i]);
end;
writeln; write('введи эталон x= '); readln(x);
(* линейный поиск*)
i:=0; while (i<=N)and(a[i]<>X) do begin i:=i+l end;
(*вывод результата*)
if i<=N then write( 'найден элемент на ',i, ' месте ') else write( 'такого элемента в массиве нет ') ;
readin
end.
Поиск делением пополам. В большинстве случаев процедура поиска применяется к упорядоченным данным (телефонный справочник, библиотечные каталоги и пр.). В подобных ситуациях эффективным алгоритмом является поиск делением пополам. В этом методе сравнение эталона Х осуществляется с элементом, расположенным в середине массива и в зависимости от результата сравнения (больше или меньше) дальнейший поиск проводится в левой или в правой половине массива.
L:=0; R:=N; while L<R do
begin
m:=(L+R) div 2;
if a[m]<X then L:=m+l else R:=m;
end;.
Например, пусть эталонный ключ х=13, а в массиве имеются следующие элементы:
а[0]=1; а[1]=3; а[2]=4; а[3]=7; а[4]=8; а[5]=9; а[6]=13; а[7]=20; а[8]=23.
Бинарный процесс поиска показан ниже:
1 3 4 7 8 9 13 20 23 - элементы массива
0 1 2 3 4 5 6 7 8- порядковые номера элементов
L m R
L m R
a[m]=x =>поиск закончен и m = 6
Программа поиска представлена ниже.
Программа 43
program poisk2; (*поиск делением пополам*)
const N=8;
type item= integer;
var a: array[0..n] of item; i, L, R, m:integer; x: item; f:
boolean;
begin
(*задание
искомого массива*)
for i:=0 to N do
begin write( 'введи
элемент a[',i, '1= '); readln(a[i])
end;
writeln; write( 'введи
эталон х= '); readln(x);
(*бинарный поиск*)
L:=0; R:=N; f:=false;
repeat m:=(L+R) div 2; if a[m]=X then f:=true;
if a[m]<X then L:=m+l
else R:=m;
writeln(m,L,R);
until (L>=R)or(f);
(*вывод результата*)
if
f then write('найден элемент на ',m, ' месте') else write('такого элемента в массиве нет ');
readln
end.
Сортировка массивов.
Как и в случае поиска определим массив данных:
var a: array [0.. N] of item
Важным условием сортировки массива большого объема является экономное использование доступной памяти. В прямых методах сортировки осуществляется принцип перестановки элементов «на том же месте». Ниже рассмотрим три группы сортировок: с помощью включения, выбора и обмена.
Сортировка с помощью включения Кто играл в карты, процедуру сортировки включениями осуществлял многократно. Как правило, после раздачи карт игрок, держа карты веером в руке, переставляет карты с места на место стремясь их расположить по мастям и рангам, например, сначала все тузы, затем короли, дамы и т.д. Элементы (карты) мысленно делятся на уже «готовую последовательность» и неправильно расположенную последовательность. Теперь на каждом шаге, начиная с i = 2, из неправильно расположенной последовательности извлекается очередной элемент и перекладывается в готовую последовательность на нужное место.
for i:=2 to N do begin
x:=a[i];
<включение х на соответствующее место готовой последовательности a[l],...,a[i]>
end
Поиск подходящего места можно осуществить одним из методов поиска в массиве, описанным выше. Затем х либо вставляется на свободное место, либо сдвигает вправо на один индекс всю левую сторону. Схематично представим алгоритм для конкретного примера:
|
Исходные элементы |
23 |
34 |
12 |
13 |
9 |
|
i=2 |
23 |
34 |
12 |
13 |
9 |
|
i=3 |
12 |
23 |
34 |
13 |
9 |
|
i=4 |
12 |
13 |
23 |
34 |
9 |
|
i=5 |
9 |
12 |
13 |
23 |
34 |
либо вставляется на свободное место, либо a[j] сдвигается вправо и процесс как бы «уходит» влево.
Программа 44
program sortirov)ca_l;
(*сортировка включением по линейному поиску*) const N=5;
type item= integer;
var a: array[l..n] of item; i, j: integer; х: item;
begin
(*задание искомого массива*)
for i:=l to N do begin write('введи
элемент a[',i,']=');
readln(a[i]) end;
for i:=l to N do begin write(a[i], ' ' );
end;
writeln;
(*алгоритм
сортировки включением*) .for i:=2 to n do begin
x:=a[i]; j:=i; a[0]:=x; (*барьер*)
while x<a[j-l] do
begin
a[j]:=a[j-l); j:=j-l;
end;
a[j]:=x; .
(for k:=l to n do write(a[k.l, ' ') end; writeln;) end;
(*вывод отсортированного массива*) for i:=l to N
do begin
.
write(a[i], ' ') ;
end;
readln;
end.
В рассмотренном примере программы для анализа процедуры пошаговой сортировки можно рекомендовать использовать трассировку каждого прохода по массиву с целью визуализации его текущего состояния. В тексте программы в блоке непосредственного алгоритма сортировки в фигурных скобках находится строка, которая при удалении скобок выполнит требуемое (параметр k
необходимо описать в разделе переменных - var k:integer). Во всех последующих программах сортировки легко осуществить подобную процедуру.
Вернемся к анализу метода прямого включения. Поскольку готовая последовательность уже упорядочена, то алгоритм улучшается при использовании алгоритма поиска делением пополам. Такой способ сортировки называют методом двоичного включения.
Программа 45
program sortirovka_2;
(*сортировка двоичным включением*) const N=5;
type item= integer;
var a: array(l..n] of item; i, j, m, L, R: integer; x: item;
begin
(*задание элементов массива*) for i:=l to N do
begin write('Bведи элемент a[',i,']= '-); readln(a[i]) ;
end;
for i:=l to N do
begin write (a[i], ' ');
end;
writeln;
(*алгоритм сортировки двоичным включением*)
for i:=2 to n do begin
x:=a(i]; L:=l; R:=i;
while L<R do begin
m:=(L+R) div 2; if a[m]<=x then L:=m+l else R:=m;
end;
for j:=i downto R+l do a(j]:=a[j-1];
a[R]:-x;
end;
(* вывод отсортированного массива*)
for i:=l to N do
begin write(a[i], ' ');
end; , readln;
end.
Один из вариантов улучшенной сортировки включением был предложен Д.Шеллом. Его метод предполагает сначала отдельную группировку и сортировку элементов, отстоящих друг от друга на некотором расстоянии, например 4 (четвертная сортировка), после первого прохода перегруппировку элементов таким образом, чтобы каждый элемент группы отстоял от другого на 2 номера, после двойной сортировки на третьем проходе одинарную (обычную) сортировку.
|
Исходные элементы |
44 |
55 |
12 |
42 |
94 |
18 |
6 |
67 |
|
Четвертная сортировка |
44 |
18 |
6 |
42 |
94 |
55 |
12 |
67 |
|
Двойная сортировка |
6 |
18 |
12 |
42 |
44 |
55 |
94 |
67 |
|
Одинарная сортировка |
6 |
12 |
18 |
42 |
44 |
55 |
67 |
94 |
Сортировка с помощью прямого выбора.
Алгоритм прямого выбора является одним из распространенных в силу своей простоты. Сначала определяют минимальный элемент среди всех элементов массива, затем его меняют местами с первым. Далее процесс повторяется с той лишь разницей, что минимальный ищется со второго и меняется со вторым и т.д.
|
1 |
2 |
3 |
4 |
5 |
|
|
12 |
15 |
17 |
11 |
13 |
i=2, min= 11 |
|
11 |
15 |
17 |
12 |
13 |
i=3.min=12 |
|
11 |
12 |
17 |
15 |
13 |
i=4, min=13 |
|
11 |
12 |
13 |
15 |
17 |
i=5,min=15. |
Программа 46
program sortirovka_3;
(*улучшенная сортировка включением - сортировка Шелла*)
const N=8; t=4;
type item= integer;
var a: array[-9..n] of item; i, j, k, s :integer; x: item;
m: l..t; h :array [l..t] of integer;
begin
(*задание искомого массива*)
for i:=l to N do
begin write('введи элемент a[',i,']=')
readln(a[i])
end;
for i:=l to N do begin write(a[i], ' ');
end;
writeln;
(*алгоритм Шелла*)
h[l]:=9; h[2]:=5; h[3]:=3; h[4]:=1;
for m:=l to t do
begin k:=h[m]; s:=-k; (*барьеры для каждого шага*)
for i:=k+l to n do
begin x:=a[i], j:=i—k; if s=0 then s:=-k;- s:=s+l;
a[s]:=x; while x<a[j] do begin a[j+k]:=a(j]; j:=j-k;
end;
a[j+k]:=x
end;
end;
(*вывод отсортированного массива*)
for i:=l to N do begin write(a[i], ' ');
end;
readln;
end.
Программа 47
program sortirovka 4;
(*сортировка прямым выбором*)
const N=5;
type item= integer;
var a: array[l..n] of item; i, j, k: integer; x: item;
begin
(*задание искомого массива*)
for i: =1 to N do
begin write('введи элемент a[', i, ']='); readln(a[i]);
end;
for i:=l to N do begin write(a[i],' ');
end;
writeln;
(*алгоритм прямого выбора*)
for i:=l to n-1 do
begin k:=i; x:=a[i]; (*поиск наименьшего элемента*)
for j:=i+l to n do (*и его индекса из a[i]...a{n]*)
if a[j]<x then begin k:=j; x:=a[k)
end;
a(k]:=a[i]; a[i]:=x;
end;
(*вывод отсортированного массива*)
for i:=l to N do begin write(a[i], ' ');
end;
readln;
end.
Улучшенный метод сортировки выбором с помощью дерева. Метод сортировки прямым выбором основан на поисках наименьшего элемента среди неготовой последовательности. Усилить метод можно запоминанием информации при сравнении пар элементов. Этого добиваются определением в каждой паре меньшего элемента за n/2 сравнений. Далее n/4 сравнений позволит выбрать меньший из пары уже выбранных меньших и т.д. Получается двоичное дерево сравнений после n-1 сравнений у которого в корневой вершине находится наименьший элемент, а любая вершина содержит меньший элемент из двух приходящих к ней вершин.
Одним из алгоритмов, использующих структуру дерева, является сортировка с помощью пирамиды (Дж.Вилльямс). Пирамида определяется как последовательность ключей hL...hR, такая, что *
hi<=h2i и hi<=h2i+l, для i=L,...,R/2.
Другими словами пирамиду можно определить как двоичное дерево заданной высоты h, обладающее тремя свойствами:
• каждая конечная вершина имеет высоту h или h-1;
• каждая конечная вершина высоты h находится слева от любой конечной вершины высоты h-1;
• значение любой вершины больше значения любой следующей за ней вершины. Рассмотрим пример пирамиды, составленной по массиву
27 9 14 8 5 11 7 2 3.
У пирамиды п вершин, их значения можно разместить в массиве а, но таким образом, что следующие за вершиной из a[i] помещаются в a[2i] и a[2i+l]. Заметим, что а[6]=11,а[7]=7, а они следуют за элементом а[3]=14 (рис.3.14).
Рис. 3.14. Пирамида
Очевидно, что если 2i > n , тогда за вершиной a[i] не следуют другие вершины, и она является конечной вершиной пирамиды.
Процесс построения пирамиды для заданного массива можно разбить на четыре этапа:
1) меняя местами а[1] и а[п], получаем 3 9 14 8 5 11 7 2 27;
2) уменьшаем n на 1, т. е. n=n-l, что эквивалентно удалению вершины 27 из дерева;
3) преобразуем дерево в другую пирамиду перестановкой нового корня с большей из двух новых, непосредственно следующих за ним вершин, до тек пор, пока он не станет больше, чем обе вершины, непосредственно за ним следующие;
4) повторяем шаги 1, 2, 3 до тех пор, пока не получим n= I.
Для алгоритма сортировки нужна процедура преобразования произвольного массива в пирамиду (шаг 3). В ней необходимо предусмотреть последовательный просмотр массива справа налево с проверкой одновременно двух условий: больше ли a[i], чем a[2i] и a[2i+l].
Полный текст программы приведен ниже.
Программа 48
program sortirovka_5;
(*улучшенная сортировка выбором - сортировка с помощью дерева*) const N=8;
type item= integer;
var a : array(l..n] of item; k, L, R: integer; x: item;
procedure sift(L,R:integer);
var i, j: integer; x,y: item;
begin i:=L; j:=2*L; x:=a[L]; if (j<R) and (a[j]<a[j+1]) then j:=j+l;
while (j<=R)and(x<a[j]) do begin y:=a[i]; a[i]:=a[j];
а[j]:=y a[i]:=a[j]; i:=j; j:=2*j;
if (j<R)and(a[j]<a(j+l]) thenj:=j+l;
end;
end;
begin
(*задание искомого массива*) for k:=l to N do begin write('введи элемент
a[',k,']=');
readln(a[k]) ;
end;
for k:=l to N do begin write(a[k], ' ');
end;
writeln;
(*алгоритм сортировки с помощью дерева*) (*построение пирамиды*) L:=(n div 2) +1; R:=n; while L>1 do begin L:=L-1; SIFT(L,R);
end;
(*сортировка*) while R>1 do begin x:=a[l]; a[l]:=a[R]; a(R]:=x;
R:=R-1; SIET(1,R);
end;
(*вывод отсортированного массива*) for k:=l to N do begin write(a[k],' ');
end;
readin;
end.
Сортировка с помощью обменов. Характерной чертой алгоритмов сортировки с помощью обмена является обмен местами двух элементов массива после их сравнения друг с другом. В так называемой «пузырьковой сортировке» проводят несколько проходов по массиву, в каждом из которых повторяется одна и та же процедура: сравнение двух последовательно стоящих элементов и их обмен местами в порядке меньшинства (старшинства) Подобная процедура сдвигает наименьшие элементы к левому концу массива. Название этого алгоритма связано с интерпретацией элементов как пузырей в сосуде с водой, обладающих весом соответствующего элемента (при этом массив надо представлять в вертикальном положении). При каждом проходе пузырьки всплывают до своего уровня.
Программа 49
program 5ortirovka_6;
(*сортировка прямым обменом - пузырьковая сортировка*)
const N=5;
type item= integer; var a: array(l,.n] of item; i, j: integer;
x: item;
begin (*задание искомого массива*)
for i:=l to N do begin write('введи элемент a[',i,']= ');
readln(a(i]);
end;
for i:=l to N do begin write(a[i], ' '); „
end;
writeln;
(*алгоритм пузырьковой сортировки*) for i:=2 to n do for j:=n downto i do begin
if a[j-l]>a[j] then begin x:=a [j-1] ;a [j-1] :=a[j]; a[j]:=x;
1 end;
end;
(*вывод отсортированного массива*) for i:=l to N do begin write(a[i], ' ');
end;
readln;
end.
Представленную программу можно легко улучшить, если учесть, что если после очередного прохода перестановок не было, то последовательность элементов уже упорядочена, т.е. продолжать проходы не имеет смысла. Читатель без труда сможет внести коррективы в программу, использовав логическую переменную, которая контролировала бы факт обмена.
Если чередовать направление последовательных просмотров, алгоритм улучшается. Такой алгоритм называют «шейкерной» сортировкой.
Программа 50
program sortirovka_7;
(*сортировка прямым обменом - шейкерная сортировка*) const N=5;
type item= integer;
var a: array[l..n] of item; i, j, k, L, R: integer; x: item;
begin (*задание искомого массива*)
for i:=l to N do begin write('введи элемент
a(',i,']=');
readln(a[i]);
end;
for i:=l to N do begin write(a[i],' end;
writeln;
(*алгоритм шейкерной сортировки*) L:=2; R:=n; k:=n;
repeat
for j:=R downto L do begin
if a[j-l]>a[j] then begin x:=a[j-l];a[j-l]:=a[j];
a(j]:=x; k:=j
end;
end;
L:=k+l;
for j:=L to R do begin
if a[j-l]>a[j] then begin x:=a(j-l];
a[j-l]:=a[j]; a[j]:=x; k:=j end;
end;
R:=k-l;
until L>R;
(*вывод отсортированного массива*)
for i:=l to N do
begin write(a[i],' ');
end; readln;
end.
Пузырьковая сортировка является не самой эффективной, особенно для последовательностей, у которых «всплывающие» элементы находятся в крайней правой стороне. В улучшенной (быстрой) пузырьковой сортировке предлагается производить перестановки на большие расстояния, причем двигаться с двух сторон. Идея алгоритма заключается в сравнении элементов, из которых один берется слева (i = 1), другой -справа (j = n). Если a[i] <= a[j] , то устанавливают j = j - 1 и проводят следующее сравнение. Далее уменьшают j до тех пор, пока a[i] > a[j]. В противном случае меняем их местами и устанавливаем i = i + 1. Увеличение i продолжаем до тех пор, пока не получим a[i] > a[j].
После следующего обмена опять уменьшаем j. Чередуя уменьшение j и увеличение i, продолжаем этот процесс с обоих концов до тех пор, пока не станет i= j. После этого этапа возникает ситуация, когда первый элемент занимает ему предназначенное место, слева от него младшие элементы, а справа - старшие.
Далее подобную процедуру можно применить к левой и правой частям массива и т.д. Очевидно, что характер алгоритма рекурсивный. Для запоминания ведущих левого и правого элементов в программе необходимо использовать стек.
Программа 51
program sortirovka_8;
(*улучшенная сортировка разделением - быстрая сортировка с рекурсией*) const N=8;
type item= integer;
var a: array(l..n] of item; i: integer;
procedure sort(L,R: integer);
var i, j :• integer; x, y: item;
begin
i:=L; j:=R; x:=a[(L+R) div 2];
repeat
while a[i]<x do i:=i+l; while x<a[j] do j:=j-l;
if i<=j then begin y:=a[i]; a[i]:=a[j];
a[j]:=y; i:=i+l; j:=j-1;
end;
until i>j ;
if L<j then SORT(L,j); if i<R then SORT(i.R); ' end;
begin , . (*задание искомого
массива*) for i:=l to N do begin write("Bвeди
элемент a[',i, ']=');
readln(a[i]);
end;
for i:=l to N do begin write(a[i],' ');
end;
writeln;
(*алгоритм быстрой сортировки*) SORT(l,n); (*рекурсивная процедура*) (*вывод отсортированного массива*) for i:=l to N do begin write(a[i],' ');
end;
readln;
end.
Сортировка файлов. Главная особенность методов сортировки последовательных файлов в том, что при их обработке в каждый момент непосредственно доступна одна компонента (на которую оказывает указатель). Чаще процесс сортировки протекает не в оперативной памяти, как в случае с массивами, а с элементами на внешних носителях («винчестере», дискете и т.п).
Понять особенности сортировки последовательных файлов на внешних носителях позволит следующий пример.
Предположим, что нам необходимо упорядочить содержимое файла с последовательным доступом по какому-либо ключу. Для простоты изучения и анализа сортировки условимся, что файл формируем мы сами, используя как и в предыдущем разделе некоторый массив данных.
Его же будем использовать и для просмотра содержимого файла после сортировки. В предлагаемом ниже алгоритме необходимо сформировать вспомогательный файл, который позволит осуществить следующую процедуру сортировки. Сначала выбираем из исходного файла первый элемент в качестве ведущего, затем извлекаем второй и сравниваем с ведущим. Если он оказался меньше, чем ведущий, то помещаем его во вспомогательный файл, в противном сл\чае во вспомогательный файл помещается ведущий элемент, а его замещает второй элемент исходного файла. Первый проход заканчивается, когда аналигичная процедура коснется всех последовательных элементов исходного файла. Ведущий элемент заносится во вспомогательный файл последним. Теперь необходимо поменять местами исходный и вспомогательный файлы. После nil проходов в исходном файле данные будут размещены в упорядоченном виде.
Программа 52
program sortirovka_faila_l;
(сортировка последовательного файла) const N=8;
type item= integer;
var a: array[l..n] of item; i,k: integer; x,y: item;
fl,f2: text; (file of item);
begin
(задание искомого массива} for i:=l to N do begin write('введи элемент а[ ',i,']=');
readin(a[i]);
end;
writein; assign(fl, 'datl.dat'); rewrite(fl);
assign(f2, 'dat2.dat'); rewrite(f2);
(формирование последовательного файла) for i:=l to N do begin writein(fl,a[i]);
end;
(алгоритм сортировки с использованием вспомогательного файла) for k:=l to (n div 2) do
begin (извлечение из исходного файла и запись во вспомогательный) reset(fl); readin(fl,x);
for i:=2 to n do begin readln(fl,y);
if x>y then writein(f2,y) else begin writein(f2,x); x:=y;
end;
end;
writein(f2,x) ;
(извлечение из вспомогательного файла и запись в исходный) rewrite(fl); reset(f2); readin(f2,x);
for i:=2 to n do begin readin(f2,у);
if x>y then writein(fl,y) else begin writein(f1,x); x:=y;
end;
end;
writeln(fl,x); rewrite(f2);
end;
(вывод результата} reset(fl);
for i:=l to N do readin(f1,a[i]);
for i:=l to N do begin write(a[i], ' ');
end;
close(fl); close(f2); readin;
end.
По сути можно в программе обойтись без массива а[1..п]. В качестве упражнения попытайтесь создать программу, в которой не используются массивы.
Многие методы сортировки последовательных файлов основаны на процедуре слияния, означающей объединение двух (или более) последовательностей в одну, упорядоченную с помощью повторяющегося выбора элементов (доступных в данный момент). В дальнейшем (чтобы не осуществлять многократного обращения к внешней памяти), будем рассматривать вместо файла массив данных, обращение к которому можно осуществлять строго последовательно. В этом смысле массив представляется как последовательность элементов, имеющая два конца, с которых можно считывать данные. При слиянии можно брать элементы с двух концов массива, что эквивалентно считыванию элементов из двух входных файлов.
Идея слияния заключается в том, что исходная последовательность разбивается на две половины, которые сливаются вновь в одну упорядоченными парами, образованными двумя элементами последовательно извлекаемых из этих двух подпоследовательностей. Вновь повторяем деление и слияние, но упорядочивая пары, затем четверки и т.д. Для реализации подобного алгоритма необходимы два массива, которые поочередно (как и в предыдущем примере) меняются ролями в' качестве исходного и вспомогательного.
Если объединить эти два массива в один, разумеется двойного размера, то программа упрощается. Пусть индексы i и j фиксируют два входных элемента с концов исходного массива, k и L - два выходных, соответствующих концам вспомогательного массива. Направлением пересылки (сменой ролей массивов) удобно управлять с помощью булевской переменной, которая меняет свое значение после каждого прохода, когда элементы а\, ..., а„ движутся на место Оп+ь ..., а^
и наоборот. Необходимо еще учесть изменяющийся на каждом проходе размер объединяемых упорядоченных групп элементов. Перед каждым последующим проходом размер удваивается. Если считать, что количество элементов в исходной последовательности не является степенью двойки (для процедуры разделения это существенно), то необходимо придумать стратегию разбиения на группы, размеры которых q и г могут не совпадать с ведущим размером очередного прохода.
В окончательном виде алгоритм сортировки слиянием представлен ниже.
Программа 53
program sortirovka_faila_2;
(сортировка последовательного файла слиянием} const N=8;
type item= integer; var a: arrayd. ,2*n] of item;
i, j, k, L, t, h, m, p, q,^r: integer; f: boolean;
begin
(задание искомого массива}
for i:=l to N do begin write( 'введи элемент а[ ',i,']='}!
readln(a[i]) ;
end;
writein;
(сортировка слиянием) f:=true; p:=l;
repeat
h:=l; т^п; if f then begin
i:=l; j:-n;k:=n+l; L:=2*n end else begin k:=l; L:=n;i:=n+l; j:-2*n
end; . repeat
if m>=p then q:=p else q:»m; m:=m-q;
if m>=p then r:=p else r:=m; m:=in-r;
while (q<>0) and (r00) do begin
if a[i]<a(j] then begin a[k]:=a(i]; k:=k+h; i:=i+l;q:=q-l
end else
begin a[k]:=a[j]; k:=k+h; j:=j-l;r:=r-l end;
end;
while r>0 do begin a[k]:=atj]; k:°k+h; j:=j-l; r:»r-l;
end;
while q>0 do begin
a[k]:=a[i]; k:°k+h; i:=i+l; q:=q-l;
end;
h:=-h; t:=k;k:=L; L:=t;
until m=0;
f:=not(f); p:°2*p;
until p>=n;
if not(f) then for i:=l to n do a[i]:=a[i+n] ;
(вывод результата} . for i:=l to N do begin write(a[i], ' ');
end;
readin;
end.
Рассмотренные два предыдущих примера иллюстрируют большие проблемы сортировки внешних файлов, если в них часты изменения элементов, например, удаления, добавления, корректировки существующих.
В подобных ситуациях эффективными становятся алгоритмы, в которых обрабатываемые элементы представляются в виде структур данных, удобных для поиска и сортировки. В качестве структур данных можно отметить, в частности, линейные списки, очереди, стеки, деревья и т.п. О них было рассказано в предыдущем разделе.
ВЕРСИИ БЕЙСИКА
Бейсик характерен необычайным обилием версий, которые иногда настолько отличаются друг от друга, что могли бы считаться разными языками.
Хотя первая официальная публикация по Бейсику создавшей его группы разработчиков Дартмутского колледжа (США) относится к 1967 г., к этому времени уже было создано три «Дартмутских версии»; первая из них относится к 1964 г. После 1967 г. к разработке этого языка подключились крупные фирмы, и были созданы версии для систем с разделением времени, для сетевых информационных систем, для мощных ЭВМ третьего поколения (включая отечественную версию «Бейсик ЕС»), для малых ЭВМ.
Большой толчок развитию Бейсика дало появление персональных компьютеров. На какое-то время Бейсик с его естественной ориентацией на трансляторы интерпретирующего типа оказался доминирующим для «персоналок» языком программирования. Бейсик оказался пригоден для первых учебных и бытовых ЭВМ с малым объемом оперативной памяти и невысоким уровнем системного программного обеспечения. Зачастую Бейсик-интерпретатор выполнял и функции операционной системы (например, бывшая популярной в России в конце 80-х - начале 90-х годов версия MSX-Бейсик учебных компьютеров «Ямаха»).
Бейсик начала 60-х годов был прост и примитивен. Он насчитывал всего порядка двух десятков команд. Несмотря на простоту работы с Бейсиком, интерфейс пользователя оставлял желать лучшего. Вся информация (текст программы, «мусор», результаты работы, сообщения) размещались на скроллирующем экране. В силу несложной процедуры разработки транслятора-интерпретатора Бейсика каждый разработчик персональных компьютеров встраивал (обычно в ПЗУ) свой вариант Бейсика.
Бурное развитие микропроцессорной техники в 70-х, затем в 80-х годах и связанные с этим проблемы совместимости заставили разработчиков задуматься о стандарте Бейсика для персональных компьютеров. Аппаратное и программное развитие позволило существенно расширить возможности языка. Бейсик стал системой программирования со всеми сервисными утилитами и инструментарием программиста.
Наибольшей популярностью для школьного и педвузовского образования приобрел Бейсик-MSX. Для большинства учебных компьютеров (Ямаха, Корвет, УКНЦ) были разработаны трансляторы версии Бейсик-MSX. Описание и практика работы с этим языком достаточно полно раскрыты в существующих популярных учебниках для вузов и школ.
Бейсик последних версий, в основном, отличается интерфейсом. Например, основное меню Турбо-Бейсика расположено в верхней строке экрана и представляет систему ниспадающих подменю, команды которых позволяют выполнять все необходимые действия по составлению, отладке и выполнению программ. В Турбо-Бейсике существуют несколько экранных режимов. Основной исходный экран представляет поле редактирования текста программы. Встроенный текстовый редактор выполняет две функции - редактирования текста и синхронной интерпретации строки. В этой связи строки нумеровать необязательно. Результаты работы программы, комментарии и сообщения интерпретатора представляются в текстовом экране (по умолчанию режим SCREEN 0). При работе с графикой изображения строятся в графическом экране, который имеет несколько режимов (режимы SCREEN n, п=2,3,...). Аналогичные возможности предусмотрены и в QBasic. Следует отметить, что в последних версиях Бейсика предусмотрены управляющие структуры. Введены операторы выбора SELECT CASE, циклические конструкции с пост- и предусловием WHILE-WEND, DO-LOOP-WHILE, DO-WHILE-LOOP, развит аппарат подпрограмм (SUB-CALL).
Особый интерес представляет система помощи - help (подсказок), имеющая контекстную структуру с возможностью копирования примеров из текста подсказок, что позволяет осваивать работу с языком программирования практически самостоятельно.
ВИДЫ БАЗ ДАННЫХ
Дадим основное определение. База данных - это реализованная с помощью компьютера информационная структура (модель), отражающая состояние объектов и их отношения.
Следует учесть, что это определение не является единственно возможным. Информатика в отношении определений чаще всего не похожа на математику с ее полной однозначностью. Если подойти к понятию «база данных» с чисто пользовательской точки зрения, то возникает другое определение: база данных - совокупность хранимых операционных данных некоторого предприятия. Все дело в том, какой аспект доминирует в рассмотрении; в данной главе первое из определений более уместно.
Поскольку основу любой базы данных составляет информационная структура, базы данных делят на три рассмотренные выше типа: табличные (реляционные), сетевые, иерархические.
Опыт использования баз данных позволяет выделить общий набор их рабочих характеристик:
• полнота
- чем полнее база данных, тем вероятнее, что она содержит нужную информацию (однако, не должно быть избыточной информации);
• правильная организация - чем лучше структурирована база данных, тем легче в ней найти необходимые сведения;
• актуальность -
любая база данных может быть точной и полной, если она постоянно обновляется, т.е. необходимо, чтобы база данных в каждый момент времени полностью соответствовала состоянию отображаемого ею объекта;
• удобство для использования - база данных должна быть проста и удобна в использовании и иметь развитые методы доступа к любой части информации.
Соответственно возможностям организации реляционных, иерархических и сетевых информационых структур, существуют и аналогичные виды баз данных. В них данные представлены в формах, адекватных соответствующим структурам. Однако иерархические и сетевые базы данных являются гораздо менее распространенными, чем реляционные и не могут быть реализованы с помощью наиболее популярных СУБД, входящих в состав программного обеспечения ЭВМ, поэтому на них далее останавливаться не будем.
Реляционные базы данных
Наиболее распространенными в практике являются реляционные базы данных. Название «реляционная» (в переводе с английского relation - отношение) связано с тем, что каждая запись в таблице содержит информацию, относящуюся только к одному конкретному объекту.
Всякое отношение должно иметь свое имя. Пусть есть отношение с названием «Альбомы группы». В этом случае структура базы данных, состоящая из одной таблицы, запишется так: Альбомы группы (название альбома, год выпуска, тип альбома, фирма). Однако чаще база данных строится на основе нескольких таблиц, связанных между собой через общие атрибуты. Пусть, например, в базе данных «Рок-энциклопедия» содержатся две таблицы - 2.3, а и 2.3, б.
Таблица 2.3, а
Музыкальные альбомы групп
|
Код альбома |
Код группы |
Название альбома |
Год выпуска |
Тип альбома |
Фирма |
|
25 |
1 |
Help! |
1965 |
Lp (English) |
Pariophone |
|
36 |
2 |
Led Zeppelin 4 |
l97l |
Lp |
Atlantic |
|
35 |
2 |
Led Zeppelin 4 - |
1970 |
Lp |
Atlantic |
|
34 |
3 |
Flash Gordon |
1980 |
Soundtrack |
EMI |
группы
|
Код группы |
Название группы |
Страна |
Дата создания |
Дата распада |
|
1 |
The Bealles |
Англия |
1963 |
I970 |
|
2 3 |
Led Zeppelin 4 Flash Gordon |
Англия Англия |
1989 199I |
- - |
создается для того, чтобы отличать альбомы друг от друга. Это очень важно, так как в таблице могут находиться альбомы с одинаковыми названиями.
Необходимость использования больше одной таблицы станет заметной, если объединить эти таблицы в одну (табл. 2.4).
Таблица 2.4 Объединение таблиц 23
|
Название группы |
Страна |
Дата создания |
Дата распада |
Название альбома |
Год выпуска |
Тип альбома |
Фирма |
|
The Beatles |
Англия |
1963 |
I970 |
With the Beatles |
1963 |
Lp |
Pariophone |
|
The Beatles |
Англия |
1963 |
I970 |
Please, please me |
1963 |
Lp |
Pariophone |
|
The Beatles |
Англия |
1963 |
I970 |
Rubber soul |
1963 |
Lp |
Pariophone |
Из таблицы 2. 4 видно, что при внесении в нее данных об альбомах определенной группы каждый раз приходится дублировать информацию первых четырех полей таблицы. Многократное сохранение в БД одних и тех же данных (название группы, страна, дата создания, дата распада) приведет к неэффективному использованию памяти, к тому же существенно возрастет вероятность ошибок при вводе данных. Разбив же данные по таблицам, можно в значительной степени избежать этих трудностей.
Через связь, определенную между этими таблицами, можно узнать
• сколько альбомов выпустила группа;
• выпускались ли альбомы у фирмы EMI;
• в каком году было выпущено максимальное количество альбомов и т.п.
Реляционные базы данных удобны еще и тем, что для получения ответов на различные запросы существует разработанный математический аппарат, который называется исчислением отношений или реляционной алгеброй. Ответы на запросы получаются путем «разрезания» и «склеивания» таблиц по строкам и столбцам. При этом ясно, что ответы также будут иметь форму таблиц.
Надо отметить, что база данных - это, собственно, хранилище информации и не более того. Однако, работа с базами данных трудоемкая и утомительная. Для создания, ведения и осуществления возможности коллективного пользования базами данных используются программные средства, называемые системами управления базами данных (СУБД).
ВИДЫ И НАЗНАЧЕНИЕ КОМПЬЮТЕРНЫХ ИГР
Игры любят все. Игра является наилучшей средой для обучения любому виду деятельности.
Характерной приметой компьютерной эры стали компьютерные игры. К ним можно относиться по-разному. С одной стороны, они могут приносить пользу как учебные средства; с другой - отнимать время (иногда очень много), отвлекать от работы. Никуда не годится играть в рабочее время, применять для этого свои дискеты, рискуя занести вирус в систему коллективного пользования и т.п. Психологи считают, что игры с изобилием сцен насилия - пусть даже выраженного в предельно условной форме - способствуют формированию у детей не самых лучших качеств. Тем не менее, компьютерные игры широко распространены. Над их созданием трудятся высокопрофессиональные программисты, художники, мультипликаторы; это достаточно процветающая подотрасль индустрии программирования. Как и многие человеческие достижения, компьютерные игры можно использовать во благо и во зло.
Компьютерные игры ориентируются на развитие у игроков определенных знаний, навыков, способностей. Как правило, в компьютерных играх от игрока требуется
• владение средствами управления, быстрота и точность манипуляций;
• быстрая и правильная реакция на происходящие события;
• чувство времени, умение выдерживать заданные временные интервалы;
• способность следить за несколькими объектами одновременно;
• знание географии игрового поля, законов игрового мира;
• знание конкретной предметной области, которая моделируется в игре;
• умение искать закономерности;
• умение предугадывать действия противника;
• знание алгоритма и стратегии выигрыша;
• способность к быстрому и максимально полному перебору основных вариантов;
• память на текущие события;
• использование прошлого опыта, что происходило в предыдущих сеансах игры;
• способность интенсивно работать в течение всего сеанса игры.
В разных играх необходимы разные качества. Привлекательность компьютерных игр определяется следующими факторами:
• интересным сценарием;
• богатым внешним оформлением;
• кажущейся простотой;
• бесконечностью игры (недостижимостью поставленной цели);
• наличием большого числа стратегий;
• разнообразием игровых ситуаций.
В компьютерных играх можно выделить следующие категории:
• игры на мастерство;
• азартные игры;
• логические игры;
• обучающие (дидактические) игры.
Игры на мастерство основаны на управлении игровыми объектами. В азартных играх исход в большей степени зависит от случайности, везения. Логические игры содержат стратегию поведения игрока, зависящую от игровых ходов соперника или от игровой ситуации. В обучающих играх объектом управления становится ученик, а целью - отработка некоторых навыков и усвоение знаний.
По способам реализации игры можно классифицировать по признакам:
· дискретные и игры с режимом реального времени;
· антагонистические и неантагонистические;
· конечные и бесконечные;
· со случайными событиями или детерминированные;
· для одного или двух и более участников;
· игры с разным уровнем сложности.
Самые распространенные компьютерные игры - пошаговые, конечные, детерминированные для двух участников, один из которых компьютер.
По структуре в компьютерных играх можно выделить три блока и три уровня:
· блок игровой среды (правила игры);
· блок взаимодействия с играющим (интерфейс);
· блок оценки игровой ситуации (анализ);
· уровень оперативный (текущее управление клавишами);
· уровень тактический (локальные цели, усложнение игры);
· уровень стратегический (конец игры, фиксация результатов).
Общая структура компютерных игр представлена на рис. 2.31.
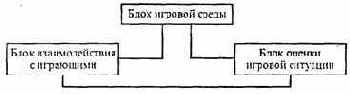
Рис. 2.31. Общая структура компьютерных игр
Блок игровой среды
- это та сцена, тот трехмерный компьютерный мир, в котором есть все, что стоит, лежит, движется, появляется и исчезает в соответствии со смыслом и законами игры.
Блок взаимодействия
- это все то в программе, что позволяет играющему изменять то, что предусмотрено блоком игровой среды.
Блок оценки - это условия для играющего и для объектов игры на игровой сцене. Это подсчет числа очков, описание или показ начальной и конечной игровой ситуации в игре.
Удается выделить три иерархических уровня, которые позволяют правильно построить схему игры: оперативный, тактический и стратегический.
Оперативный уровень - это изменение объектов на игровой сцене посредством нажатия клавиш или управляющего устройства (мышь, джойстик). Результатом действия оперативного уровня должно быть отображение всех перемещений и изменений на экране дисплея.
Тактический уровень включает и оперативный. Действия на этом уровне ведут к достижению некоторой вполне определенной локальной цели. Изменения сложности игры, темпа, уровня происходят на этом этапе.
Стратегический уровень
включает тактический и содержит несколько самостоятельных блоков: ввод на игровую схему всех объектов для определения, задания и визуализации их начальных параметров, проверка критериев окончания игры, фиксации и визуализации результатов всей игры в целом и результатов прошлых игр.
ВИДЫ СТРУКТУР ДАННЫХ
В информатике совокупность взаимосвязанных данных называется информационной структурой, или структурой данных. В нашем примере объектами модели являются музыкальные альбомы. Свойства же этих объектов находятся в столбцах таблицы («Название альбома», «Год выпуска», «Тип альбома», «Фирма»), их называют атрибутами объектов. Таким образом, каждая строка таблицы - есть совокупность атрибутов объекта. Такую строку называют записью, а столбец - полем записи.
Помимо сведений, указанных в атрибутах, табличная организация данных позволяет получить дополнительную информацию. К примеру, нетрудно узнать (в предположении, что наша табл. 2.2 заполнена данными):
• какая группа выпустила больше альбомов за определенный период;
• число альбомов данной группы;
• сколько имеется альбомов типа Soundtrack (музыка к фильму);
• какая фирма выпустила наибольшее число альбомов данной группы.
Табличная организация данных называется также реляционной. Кроме табличной структуры данных существуют другие виды структурной организации данных.
Для иерархических структур (рис.2.22) характерна подчиненность объектов нижнего уровня объектам верхнего уровня. Важно отметить, что в дереве, между верхними и нижними объектами, задано отношение «один ко многим» (т.е. одной группе соответствует много альбомов, одному альбому соответствует много песен).
Рис. 2.22. Пример иерархической организации данных
Несмотря на то, что в атрибутах, описывающих песню, нет названия альбома, глядя на дерево по линиям связи можно сказать, какая песня принадлежит альбому. Благодаря линиям связи можно определить принадлежность альбома группе. Из данной иерархической структуры можно узнать:
• в каком альбоме больше песен;
• число альбомов выпущенных группой;
• есть ли в альбомах одинаковые песни и т.д.
Сетевую структуру данных можно представить в виде схемы, рис. 2.23.
Рис. 2.23. Пример сетевой организации данных
Глядя на рис. 2.23, можно определить, какими инструментами владеет музыкант, является ли он вокалистом. В этом случае есть два уровня взаимосвязанных объектов, но отношение между ними «многие ко многим».
Пусть в этой сетевой структуре данные о музыкантах и «инструментах» состоят из следующих атрибутов: музыкант - ФИО, рост, цвет волос, время рождения; инструмент- название инструмента, какой фирмой изготовлен инструмент.
Тогда схема позволяет ответить на следующие вопросы:
• гитары какой фирмы предпочитает большинство музыкантов;
• какой музыкант владеет наибольшим количеством инструментов и др.
Построение структуры данных происходит в следующем порядке:
• определяются объекты описания;
• определяются структуры этих объектов;
• выбирается тип структуры, отображающий отношения между объектами (табличная, иерархическая, сети);
• строится конкретная информационная структура.
§ ВНЕШНИЕ УСТРОЙСТВА ЭВМ: ФИЗИЧЕСКИЕ ПРИНЦИПЫ И ХАРАКТЕРИСТИКИ
Внешние (или, по другому, периферийные) устройства ЭВМ прошли огромный путь в своем развитии. Существуй машина времени, инженеры-конструкторы и пользователи ЭВМ 50-х годов, увидев принтер, вряд ли поверили бы, что этот миниатюрный настольный аппарат может делать гораздо больше, чем его предок ростом с человека - АЦПУ (авгоматическое цифровое печатающее устройство), и вообще не поняли бы, чем занимается сканер или «мышь». Возможности компьютера в значительной степени определяются номенклатурой и производительностью внешних устройств.
ВНЕШНИЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА
Внешние запоминающие устройства (ВЗУ) обеспечивают долговременное хранение программ и данных. Наиболее распространены следующие типы ВЗУ: накопители на магнитных дисках (НМД); их разновидности - накопители на гибких магнитных дисках (НГМД) и накопители на жестких магнитных дисках (НЖМД); накопители на магнитных лентах (НМЛ); накопители на оптических дисках (НОД).
Соответственно, физическими носителями информации, с которыми работают эти устройства, являются магнитные диски (МД), магнитные ленты (МЛ) и оптические диски (ОД).
Принцип записи информации на магнитных носителях основан на изменении намагниченности отдельных участков магнитного слоя носителя (диска, ленты). Запись осуществляется с помощью магнитной головки: электрические сигналы, возникающие под управлением электронного блока, возбуждают в ней магнитное поле, воздействующее на носитель и оставляющее намагниченные участки на заранее размеченных дорожках. При считывании информации эти намагниченные участки индуцируют в магнитной головке слабые токи, которые превращаются в двоичный код, соответствующий ранее записанному.
Накопители на магнитных дисках включают в себя ряд систем:
• электромеханический привод, обеспечивающий вращение диска;
• блок магнитных головок для чтения-записи;
• системы установки (позиционирования) магнитных головок в нужное для записи или чтения положение;
• электронный блок управления и кодирования сигналов.
НГМД - устройство со сменными дисками (их часто называют «дискетами»). Несмотря на относительно невысокую информационную емкость дискеты, НГМД продолжают играть важную роль в качестве ВЗУ, поскольку поддерживают ряд функций, которые не обеспечивают другие накопители. Среди них отметим
• возможность транспортировки информации на любые расстояния;
• обеспечение конфиденциальности информации (дискету можно положить в карман сразу после окончания сеанса работы).
Дискета - гибкий тонкий пластиковый диск с нанесенным (чаще всего на обе стороны) магнитным покрытием, заключенный в достаточно/тверды и - картонный или пластиковый - конверт для предохранения от механических повреждений.
Информация на диск наносится вдоль концентрических окружностей - дорожек. Каждая дорожка разбита на несколько секторов (обычно 9 или 18) - минимально возможных адресуемых участков. Стандартная емкость сектора - 512 байт. На двухсторонней дискете две одинаковые дорожки по обе стороны диска образуют цилиндр. Процедура разметки нового диска - нанесение секторов и дорожек -называется форматированием. Иногда приходится прибегать к переформатированию диска, на котором уже есть информация; последняя в таком случае практически обречена на уничтожение.
Тип дискеты обычно указывается на ее конверте:
DS (double side) - двухсторонняя;
DD (double density) - двойной плотности;
HD (high density) - высокой плотности.
Возможны сочетания типа DS/DD, DS/HD и др.
Стандартные размеры (диаметры) дискет 133 мм (5,25 дюйма; постепенно выходят из эксплуатации) и 89 мм (3,5 дюйма). Появились, но пока не получили широкого распространения, дискеты диаметром 51 мм.
Важнейшая, с точки зрения пользователя, характеристика дискеты - информационная емкость. Чаще всего она находится в диапазоне от одного до полутора мегабайт, хотя созданы дискеты с емкостью до 10 Мбайт. Специальные дискеты для резервного копирования (так называемые Zip-диски, для работы с которыми нужны особые дисководы) имеют емкость 100 Мбайт и более. Другие важнейшие характеристики - скорость доступа к определенному участку информации и скорость записи или считывания информации - определяются не столько самой дискетой, сколько возможностями НГМД. Доступ к информации осуществляется за время в диапазоне от 0,1 с до 1 с (что очень велико по сравнению с другими типами дисководов), скорость чтения/записи порядка 50 кбайт/с, что по современным представлениям весьма немного.
Жесткий диск
сделан из сплава на основе алюминия и также покрыт магнитным
слоем. Он помещен в неразборный корпус, встроенный в системный блок компьютера. По всем профессиональным характеристикам жесткие диски (и соответствующие накопители) значительно превосходят гибкие: емкость от 20 Мбайт до 10 Гбайт (реально диски с емкостью меньшей, чем 1 Гбайт, давно не выпускаются), время доступа к конкретной записи в диапазоне от 1 до 100 миллисекунд (мс), скорость чтения/записи порядка 1 Мбайта/с.
Скорость вращения дисков велика, обычно 3600 об/мин, что и обеспечивает относительно короткое время доступа. Однако, жесткий диск не предназначен для транспортировки информации, и это не позволило накопителям на жестких дисках вытеснить НГМД.
Первые накопители на оптических дисках появились в начале 70-х годов, но широкое распространение получили значительно позже. Существует несколько разновидностей оптических дисков, предназначенных для устройств, допускающих только чтение (CD-ROM, т.е. Compact Disk Reed Only Memory - компакт-диск только для чтения), для устройств, допускающих хотя бы однократную запись информации на рабочем месте пользователя и для устройств, позволяющих, подобно накопителям на магнитных дисках, многократную перезапись информации. CD-ROM диск, запись на который производится один раз при его создании и не может быть изменена, представляет собой прозрачную поликарбонатную (вид стекла) пластинку, одна сторона которой покрыта тончайшей алюминиевой пленкой, играющей роль зеркального отражателя, поверх которой нанесен защитный слой лака. Информация на ней представляется подобно тому, как на старых граммофонных пластинках - чередованием углублений и пиков, однако не в аналоговом, а в цифровом (двоичном) коде. Этот рельеф создается при производстве механическим путем (контактом с твердой пластинкой - матрицей). Информация наносится вдоль тончайших дорожек (радиальная плотность записи более 6000 дорожек/см, что в несколько десятков раз больше, чем для гибкого диска). Считывание информации осуществляется путем сканирования дорожек лазерным лучом, который по-разному отражается от углублений и пиков (по этому отражению восстанавливается записанный двоичный код). Вдоль дорожек оптического диска со скоростью 200 - 500 раз в минуту пробегает лазерный луч. При создании дисков, позволяющих вести многократную перезапись, доминирует магнито-оптический принцип (CD-МО диски). В основу положен следующий физический принцип: коэффициент отражения лазерного луча от по-разному намагниченных участков диска с особым образом нанесенным магнитным покрытием различен.
Таким образом запись на МО-диски магнитная, а считывание - оптическое (лазерным лучом).
Профессиональные характеристики оптических дисков, в общих чертах таковы: емкость записи и скорость доступа к информации того же порядка, что у жестких дисков. По надежности хранения информации оптические диски в настоящее время не имеют себе равных.
Все вместе взятое и определяет место НОД в современном мире информационных технологий: от очень важных, но все-таки факультативных, устройств они становятся обязательной принадлежностью компьютеров. По мере снижения стоимости оборудования CD-МО диски могут вытеснить гибкие магнитные диски, так как, обладая значительно превосходящими профессиональными характеристиками, обеспечивают все функции ГМД. Заметим, что ситуация в .этой области меняется чрезвычайно быстро.
Накопители на магнитных лентах имели огромное значение для ЭВМ первых поколений. Собственно, поначалу кроме них надежных накопителей информации большой емкости вообще не было. По мере развития ЭВМ НМЛ оттеснялись на периферию в списке ВЗУ, но свое устойчивое место занимают по сей день (хотя пользователям персональных компьютеров это не очень заметно). Ясно, что по скорости доступа к информации НМЛ всегда будут многократно проигрывать дисковым накопителям - ведь для того, чтобы считать информацию на некотором месте ленты, необходимо отмотать предшествующий ее кусок с начала. Однако по-прежнему на лентах хранят большие объемы информации, которая не является оперативной, но требует очень надежного хранения, а также конфиденциальности.
На персональных компьютерах иногда используют специальный кассетный накопитель, размеры которого совпадают с размерами НГМД и который можно вставить на место последнего - так называемый стриммер. Он удобен, например, для переноса информации с жесткого диска одного компьютера на другой, долговременного хранения особо ценных системных и личных программ и данных.
ВНУТРЕННЯЯ ОРГАНИЗАЦИЯ МИКРОПРОЦЕССОРА
Перечислим основные функции микропроцессора:
• выборка команд из ОЗУ;
•декодирование команд (т.е. определение назначения команды, способа ее исполнения и адресов операндов);
• выполнение операций, закодированных в командах;
• управление пересылкой информации между своими внутренними регистрами, оперативной памятью и внешними (периферийными) устройствами;
• обработка внутрипроцессорных и программных прерываний;
• обработка сигналов от внешних устройств и реализация соответствующих прерываний;
• управление различными устройствами, входящими в состав компьютера.
Внутреннее устройство микропроцессоров очень сложно (вспомним три миллиона транзисторов в «Pentium»). Даже если попытаться рассмотреть наиболее общую схему основных функциональных узлов, и то получится достаточно сложная картина. К тому же внутреннее устройство МП сильно зависит от его марки, а стало быть изучение структуры одного процессора не обязательно помогает понять работу другого. Следует признать нецелесообразным для пользователя (и даже, может быть, для программиста) изучение инженерных деталей процессора современной ЭВМ, и ограничиться, как это принято делать, только теми функциональными узлами, которые доступны программно. При таком подходе оказывается, что МП имеют много общего, и становятся отчетливо видны некоторые закономерности их внутреннего устройства. Кроме того, исчезает пугающая сложность и возникает приятное и полезное чувство, что компьютер - это не какая-то там «вещь в себе» и его поведение можно понять.
Итак, что же представляет собой микропроцессор с точки зрения программиста? Рассмотрение начнем в наиболее общем виде, не конкретизируя пока тип МП.
Ответ на поставленный вопрос, как ни странно, будет чрезвычайно прост: для программиста любой процессор состоит из набора регистров памяти различного назначения, которые определенным образом связаны между собой и обрабатываются в соответствии с некоторой системой правил. Конечно, программисту доступна не вся внутренняя память процессора: есть множество рабочих (программно-недоступных) регистров, использующихся только во время выполнения команд и т.п.; их мы рассматривать не будем.
Обсуждение внутренних регистров микропроцессора начнем с наиболее важных: счетчика адреса команд, указателя стека и регистра состояния. Наличие счетчика адреса команд, как уже говорилось выше, было предложено еще в работах фон Неймана. Роль счетчика состоит в сохранении адреса очередной команды программы и автоматическом вычислении адреса следующей. Благодаря наличию программного счетчика в ЭВМ реализуется основной цикл исполнения последовательно расположенных команд программы. Заметим, что не во всех МП счетчик команд программно доступен.
В указателе стека
хранится адрес начала специальным образом организуемого участка памяти стека, описанного в следующем параграфе; роль указателя стека в функционировании процессора достаточно велика.
Наконец, регистр состояния процессора. Для разных МП он может называться по-разному (например, слово состояния процессора, регистр флагов и т.п.), но суть его всегда одна: в этом регистре хранятся сведения о текущих режимах работы процессора. Сюда же помещается информация о результатах выполняемых команд, например, равен ли результат нулю, отрицателен ли он, не возникли ли ошибки в ходе операции и т.п. Использование и анализ информации в этом очень важном регистре происходит побитно; иными словами, каждый бит регистра состояния имеет самостоятельное значение. Содержание регистра состояния МП всегда старается сохранить в первою очередь сразу после значения командного счетчика.
Помимо рассмотренных выше, каждый МП имеет набор рабочих регистров, в которых хранятся текущие обрабатываемые данные или их адреса в ОЗУ. У некоторых процессоров регистры функционально равнозначны (классическим примером служит процессор машин семейства PDP). в других (к ним принадлежит все интел-ловское семейство МП) назначение регистров достаточно жестко оговаривается. В последнем случае выделяется особый регистр, который принято называть аккумулятором.. В нем производятся все основные операции и сохраняется их результат
Завершая разговор о регистрах, укажем на существование определенных связей между ними: информация из одного может передаваться в другой.
Для машин с равноправными регистрами передача данных возможна между любыми регистрами, для остальных - между строго определенными парами. Так или иначе (в худшем случае за несколько машинных команд) информацию из одного регистра МП всегда можно перенести в другой.
Разрядность регистров
МП существенно влияет на возможности всей ЭВМ. Поэтому уточним понятие «разрядность ЭВМ». Оно включает
• разрядность внутренних регистров микропроцессора (m);
• разрядность шины данных (n);
• разрядность шины адреса (k).
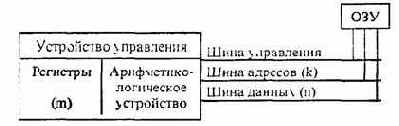
Рис. 4.12. Обмен информацией между процессором и основной памятью
Схема обмена информацией между микропроцессором и ОЗУ представлена на рис. 4.12. Данные поступают из ОЗУ в регистры процессора и наоборот по шине данных; по шине адреса передается информация о месте хранения данных в ОЗУ. Разрядности этих шин могут не совпадать: например, упомянутый выше МП «Intel 8088» характеризовался значениями m/n/k = 16/8/20. Когда говорят, не вникая в детали, «16-разрядная ЭВМ», то имеют в виду значение т. Поскольку объем адресного пространства ОЗУ, контролируемого МП, равен 2k, то понятно стремление увеличить разрядность шины адреса.
ВОСЬМЕРИЧНАЯ И ШЕСТНАДЦАТИРИЧНАЯ СИСТЕМЫ СЧИСЛЕНИЯ
С точки зрения изучения принципов представления и обработки информации в компьютере, обсуждаемые в этом пункте системы представляют большой интерес.
Хотя компьютер «знает» только двоичную систему счисления, часто с целью уменьшения количества записываемых на бумаге или вводимых с клавиатуры компьютера знаков бывает удобнее пользоваться восьмеричными или шестнадцатиричными числами, тем более что, как будет показано далее, процедура взаимного перевода чисел из каждой из этих систем в двоичную очень проста - гораздо проще переводов между любой из этих трех систем и десятичной.
Перевод чисел из десятичной системы счисления в восьмеричную производится (по аналогии с двоичной системой счисления) с помощью делений и умножений на 8. Например, переведем число 58,32(10):
58 : 8 = 7 (2 в остатке),
7 : 8 = 0 (7 в остатке).
0,32 • 8 = 2,56,
0,56 • 8 = 4,48,
0,48-8=3,84,...
Таким образом,
58,32(10) =72,243... (8)
(из конечной дроби в одной системе может получиться бесконечная дробь в другой).
Перевод чисел из десятичной системы счисления в шестнадцатеричную производится аналогично.
С практической точки зрения представляет интерес процедура взаимного преобразования двоичных, восьмеричных и шестнадцатиричных чисел. Для этого воспользуемся табл. 1.6 чисел от 0 до 15 (в десятичной системе счисления), представленных в других системах счисления.
Для перевода целого двоичного числа в восьмеричное необходимо разбить его справа налево на группы по 3 цифры (самая левая группа может содержать менее трех двоичных цифр), а затем каждой группе поставить в соответствие ее восьмеричный эквивалент. Например:
11011001= 11011001, т.е. 11011001(2) =331(8).
Заметим, что группу из трех двоичных цифр часто называют «двоичной триадой».
Перевод целого двоичного числа в шестнадцатиричное производится путем разбиения данного числа на группы по 4 цифры - «двоичные тетрады»:
1100011011001 = 1 1000 1101 1001, т.е. 1100011011001(2)= 18D9(16).
Для перевода дробных частей двоичных чисел в восьмеричную или шестнадцатиричную системы аналогичное разбиение на триады или тетрады производится от точки вправо (с дополнением недостающих последних цифр нулями):
0,1100011101(2) =0,110 001 110 100 = 0,6164(8),
0,1100011101(2) = 0,1100 0111 0100 = 0,C74(16).
Перевод восьмеричных (шестнадцатиричных) чисел в двоичные производится обратным путем - сопоставлением каждому знаку числа соответствующей тройки (четверки) двоичных цифр.
Таблица 1.6 Соответствие чисел в различных системах счисления
|
Десятичная |
Шестнадцатиричная |
Восьмеричная |
Двоичная |
|
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
|
2 |
2 |
2 |
10 |
|
3 |
3 |
3 |
11 |
|
4 |
4 |
4 |
100 |
|
5 |
5 |
5 |
101 |
|
6 |
6 |
6 |
110 |
|
7 |
7 |
7 |
111 |
|
8 |
8 |
10 |
1000 |
|
9 |
9 |
11 |
1001 |
|
10 |
А |
12 |
1010 |
|
11 |
В |
13 |
L011 |
|
12 |
С |
14 |
1100 |
|
13 |
D |
15 |
1101 |
|
14 |
E |
16 |
1110 |
|
15 |
F |
17 |
1111 |
Арифметические действия с числами в восьмеричной и шестнадцатиричной системах счисления выполняются по аналогии с двоичной и десятичной системами. Для этого необходимо воспользоваться соответствующими таблицами. Для примера табл. 1.7 иллюстрирует сложение и умножение восьмеричных чисел.
Рассмотрим еще один возможный способ перевода чисел из одной позиционной системы счисления в другую - метод вычитания степеней. В этом случае из числа последовательно вычитается максимально допустимая степень требуемого основания, умноженная на максимально возможный коэффициент, меньший основания; этот коэффициент и является значащей цифрой числа в новой системе.
Например, число 114(10):
114 - 26 = 114 – 64 = 50,
50 - 25 = 50 – 32 = 18,
18 - 24 = 2,
2 - 21 = 0.
Таким образом, 114(10) = 1110010(2).
114 – 1 • 82 = 114 – 64 = 50,
50 – 6 • 81 = 50 – 48 = 2,
2 – 2 • 8° = 2 – 2 = 0.
Итак, 114(10)= 162(8).
Таблица 1.7 Таблицы сложения и умножения в восьмеричной системе
Сложение Умножение

Контрольные вопросы
1. В чем отличие позиционной системы счисления от непозиционной?
2. Каковы способы перевода чисел из одной системы счисления в другую?
3. В чем заключается преимущество использования восьмеричной и шестнадцатиричной систем счисления в вычислительной технике?
4. Как выглядят таблицы сложения и умножения в шестнадцатиричной системе?
ВВОД-ВЫВОД ДАННЫХ
До сих пор рассматривался ввод и вывод данных в лисповских программах через параметры функций и свободные переменные. Для организации диалога человека с программой в Лиспе существуют специальные функции READ и PRINT.
Для вывода результатов можно использовать функцию PRINT. Это функция с одним аргументом, которая сначала вычисляет значение аргумента, а затем выводит это значение.
Например:
(PRINT (* 2 2))
Результат: 4.
Перед выводом происходит переход на новую строку.
Функция READ читает и возвращает выражение: (READ). Как только интерпретатор встречает такое предложение, вычисления приостанавливаются до тех пор, пока не будет введен какой-либо символ или целиком выражение. Аргументов у функции READ нет, ее использование построено на побочном эффекте, состоящем именно во вводе выражения. Прочитанное выражение можно сохранить для следующего использования и обработки, например, так:
(setq input (read));
прочитанное READ выражение присваивается переменной input.
Лисповские операторы ввода-вывода очень гибки, их можно использовать в качестве аргументов других функций. Для более эстетичного оформления вывода можно использовать функции PRINC, печатающую строку без окаймляющих кавычек и со специальными символами, а также TERPRI, переводящую строку.
Для форматного вывода (в соответствии с некоторым образом) существует функция FORMAT, обладающая гибкими возможностями, описанными в руководствах по языку Лисп.
Помимо стандартных устройств ввода-вывода, может осуществляться обработка файлов на магнитных носителях, загружаться из файлов определения функций и т.д.
и программ) для решения системы
1. Используя принцип проектирования сверху-вниз постройте блок-схему и программ) для решения системы линейных алгебраических уравнений методом Гаусса.
2. Разработайте алгоритм и программу поиска тура коня по другой стратегии, например, по случайному выбору очередного хода из числа возможных.
ЗАКОНЫ ПОДОБИЯ
Рассмотрим эту известную задачу с учетом сопротивления воздуха. Будучи брошенным под углом ? к горизонту с начальной скоростью v0, тело летит, если не учитывать сопротивления воздуха, по параболе, и через некоторое время падает на землю. Напомним элементарное решение этой задачи. Разложим скорость на горизонтальную и вертикальную составляющие:
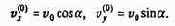
Поскольку движение по вертикали происходит под действием постоянной силы тяжести, то оно является равнозамедленным до достижения верхней точки на траектории и равноускоренным - после нее; движение же по горизонтали является равномерным. Из формул равноускоренного движения vy
= v

= 0, то время достижения верхней точки на траектории
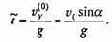
Высота этой точки
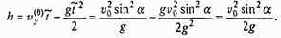
Полное время движения до падения на землю 2


тело пройдет путь
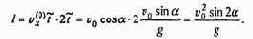
Для нахождения траектории достаточно из текущих значений x
и у исключить t:
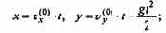
следовательно,
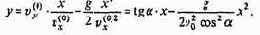
Уравнение (7.11) - уравнение параболы.
Полученные формулы могут, в частности, послужить для тестирования будущей компьютерной программы. При достаточно большой начальной скорости сопротивление воздуха может значительно изменить характер движения. Прежде чем выписывать уравнения, вновь оценим, какая из составляющих силы сопротивления - линейная или квадратичная по скорости - дает больший вклад в эту силу, и нельзя ли одной из этих составляющих пренебречь. Оценку проведем для шарика; по порядку величины оценка не зависит от формы тела. Итак, шарик радиусом r ? 0,1 м, движущийся со скоростью ~ 1 м/с, испытывает в воздухе линейную (стоксову) силу сопротивления
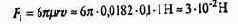
и квадратичную силу сопротивления
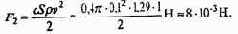
Величины F1 и F2 сопоставимые (как принято говорить, «одного порядка», так как они различаются менее, чем в 5 раз). При увеличении размера тела F2
растет быстрее, чем F1 (F1 ~ r, F2 ~ r2),
при увеличении скорости F2
также растет быстрее, чем F1
(F1 ~ v, F2 ~ v2). Таким образом, если мы моделируем движение брошенного мяча, камня, то необходимо в уравнениях удерживать обе составляющие силы сопротивления, но если мы захотим моделировать полет снаряда, выпущенного из орудия, где скорость полета почти на всем его протяжении сотни метров в секунду, то линейной составляющей силы сопротивления можно пренебречь. Проецируя уравнение

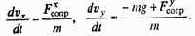
Поскольку в каждой точке траектории сила сопротивления направлена по касательной к траектории в сторону, противоположную движению, то
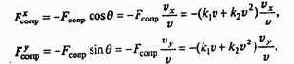
где ? -
угол между текущим направлением скорости и осью х. Подставляя это в уравнение и учитывая, что

получаем уравнения движения в переменных vx, vy.

Поскольку представляет несомненный интерес и траектория движения, дополним систему (7.12) еще двумя уравнениями
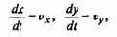
и, решая их совместно с (7.12), будем получать разом четыре функции: vx(t), vy(t), x(t), y(t).
Прежде чем дать пример решения обсуждаемой задачи, покажем очень полезный прием, чрезвычайно популярный в физическом моделировании, называемый обезразмериванием.
При решении конкретных задач мы пользуемся определенной системой единиц (СИ), в которой далеко не все числовые значения лежат в удобном диапазоне. Кроме того, абсолютные значения величин дают мало информации для качественного понимания. Скорость 15 м/с - много это или мало? Все дело в том, по сравнению с чем. Именно в сравнении с чем-то привычным и понятным мы обычно и воспринимаем слова «много» и «мало», даже если делаем это бессознательно. Идея обезразмеривания заключается в переходе от абсолютных значений расстояний, скоростей, времен и т.д. к относительным, причем отношения строятся к величинам, типичным для данной ситуации. В рассматриваемой задаче это особенно хорошо просматривается. В самом деле, при отсутствии сопротивления воздуха мы имеем значения l, h, t, определенные выше; сопротивление воздуха изменит характер движения, и если мы введем в качестве переменных величины
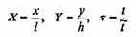
- безразмерные расстояния по осям и время, - то при отсутствии сопротивления воздуха эти переменные будут изменячься в диапазоне от 0 до 1, а в задаче с учетом сопротивления отличия их максимальных значений от единицы ясно характеризуют влияние этого сопротивления. Для скоростей естественно ввести безразмерные переменные, соотнося проекции скорости на оси x и у с начальной скоростью v0:
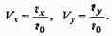
Покажем, как перейти к безразмерным переменным в одном из наших уравнений, например, во втором уравнении системы (7.12). Имеем:
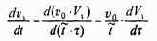
(так как постоянный множитель можно вынести за знак производной). Подставляя это в уравнение, получаем
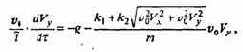
или
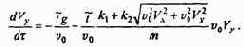
Подставляя
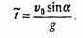
получаем
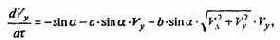
где безразмерные комбинации параметров, входящих в исходные уравнения,
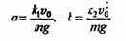
Выполним обезразмеривание во всех уравнениях (7.12), (7.13) (рекомендуем читателям проделать эту процедуру самостоятельно). В результате получим
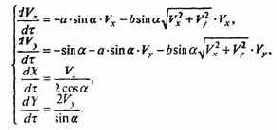
Начальные условия для безразмерных переменных таковы:
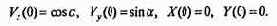
Важнейшая роль обезразмеривания - установление законов подобия. У изучаемого движения есть множество вариантов, определяемых наборами значений параметров, входящих в уравнения (7.12), (7.13) или являющихся для них начальными условиями: k1, k2, m, g, v0, а. После обезразмеривания переменных появляются безразмерные комбинации параметров - в данном случае a, b, ? -
фактически определяющие характер движения. Если мы изучаем два разных движения с разными размерными параметрами, но такие, что а, b
и ? одинаковы, то движения будут качественно одинаковы. Число таких комбинаций обычно меньше числа размерных параметров (в данном случае вдвое), что также создает удобство при полном численном исследовании всевозможных ситуаций, связанных с этим процессом. Наконец, как уже отмечалось, величины Vx, Vy, X, Y, ? физически легче интерпретировать, чем их размерные аналоги, так как они измеряются относительно величин, смысл которых очевиден.
Прежде чем предпринимать численное моделирование, отметим, что при учете лишь линейной составляющей силы сопротивления модель допускает аналитическое решение. Система уравнений (7.14) при b = 0 достаточно элементарно интегрируется и результаты таковы:
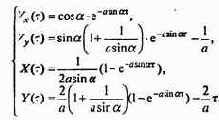
Исключая из двух последних формул время, получаем уравнение траектории:
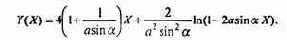
Заметим, что эта формула не из тех, которые привычно визуализируются, например, по сравнению с совершенно отчетливой формулой (7.11), и здесь компьютер может быть полезен в том, чтобы составить ясное представление о влиянии линейной части силы сопротивления на изучаемое движение.
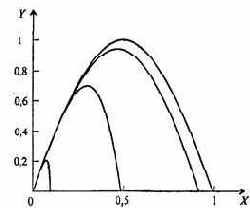
Рис. 7.8. Семейство траекторий при ? = 45°
и значениях ?, равных 0,01; 0,1; 1 и 10 (кривые - справа налево)
На рис. 7.8 приведены траектории четырех движений с разными значениями параметра ?, характеризующего трение. Видно, как сильно оно влияет на движение -
его форму, расстояния по вертикали и горизонтали. Общее исследование при произвольных значениях а и b поможет выполнить приведенная ниже программа.
Фактически представлены две программы: при активизации первого или второго блока. В первом случае она выдает результаты численного моделирования в виде таблицы значений безразмерных скоростей и координат при фиксированном наборе параметров а, b
и ?, значения которых устанавливаются в разделе определения констант. При взятии в фигурные скобки первого блока и активизации второго (т.е. снятия фигурных скобок) программа выдает в графическом режиме семейство траекторий, отличающихся значениями одного из трех безразмерных параметров (в данном случае b).
Программа 148.
Реализация модели «Полет тела, брошенного под углом к горизонту»
Program Pod Uglom;
Uses Crt, Graph;
Type G =
Array[1..4] Of Real;
Const A = 0; В =0.1; (параметры модели)
Al = Pi / 4; (угол - параметр модели}
Н = 0.001; Нрr = 0.1; (шаг интегрирования и шаг вывода результатов)
Var N, I, J, M, L, К : Integer;
Y0, Y : G; Х0, X, Xpr, A1, B1, Cosinus, Sinus : Real; LS : String;
Function Ff(I : Integer; X : Real; Y : G) : Real;
{ описание правых частей дифференциальных уравнений}
Begin
Case I Of
1: Ff:=-A1*Sinus*Y[l]-Bl*Sinus*Sqrt(Sqr(Y(l])+Sqr(Y[2]))*Y[1];
2: Ff:=-Sinus-A1*Sinus*Y[1]-B1*Sinus*Sqrt(Sqr(Y(1])+Sqr(Y[2]))*Y[2];
3: Ff:=Y[1]/(2*Cosinus);
4: Ff:=2*Y[2]/Sinus
End
End;
Procedure Runge_Kut (N: Integer; Var X: Real; Y0: G; Var Y: G; Н: Real);
(метод Рунге-Кутта четвертого порядка)
Var I : Integer; Z, K1, K2,
КЗ, К4 : G;
Procedure Right(X : Real; Y : G; Var F : G) ;
{вычисление правых частей дифференциальных уравнений}
Var I : Integer;
Begin
For I := 1 To N Do F[I] := Ff(I, X, У)
End;
Begin Right(X, Y0, K1); X := X + Н / 2;
For I := 1 To N Do Z[I]:=Y0[I]+H*K1[I]/2; Right(X, Z, K2);
For I := 1 To N Do Z[I]:=YO[I]+H*K2[I]/2; Right(X, Z, КЗ); Х:=Х+Н/2;
For I := 1 To N Do Z[I] := Y0[I] + H * КЗ [I]; Right (X, Z, К4);
For I := 1 To N Do
Y[I]:=Y0[I]+H*(K1[I]+2*K2[I]+2*K3[I]+K4[I])/6;
End;
{следующий блок - для получения численных результатов при одном наборе параметров}
{Begin
Sinus := Sin(Al); Cosinus := Cos(Al); Al := A; Bl := B; ClrScr;
N:=4; X0:=0; Y0[l]:=Cosinus; Y0[2]:=Sinus; Y0[3]:=0; Y0[4]:=0;
WriteLn(' время скорость координаты');
WriteLn; X := Х0; Xpr := 0; Y[4] := Y0[4];
While Y[4] >= 0 Do
Begin
If X >= Xpr Then
Begin
WriteLn ('t=', X : 6 : 3, ' Vx='. Y0[l] : 6 : 3, ' Vy=',
Y0[2] : 6 : 3. ' X=', y0[3] : 6 : 3, ' Y=', Y0[4] : б
: 3) ;
Xpr := Xpr + Hpr
End;
Runge_Kut(N, X, Y0, Y, H); Y0 := Y
End;
WriteLn; WriteLn('для продолжения нажмите любую клавишу');
Repeat Until KeyPressed
End.}
{следующий блок - для изображения траекторий при нескольких наборах параметров)
Begin
DetectGraph (J, M); InitGraph (J, M, '');
L := 1; Al := A; Bl := В; Sinus := Sin(Al); Cosinus := Cos(Al);
While L < 5 Do
Begin
N
:= 4; (Количество уравнений в системе)
Х0 := 0; Y0[l] := Cosinus; (Начальные условия}
Y0[2] := Sinus; Y0[3] := 0; Y0[4] := 0:
SetColor(L); Line(400, 50 + 20 * (L - 1), 440, 50 + 20 * (L - 1));
OutTextXY(450, 50 + 20 * (L - 1), '1 = ');
Str(L, LS); OutTextXY(480, 50+20*(L-l), LS); X:=X0; Y[4]:=Y0[4];
While Y[4] >= 0 Do
Begin
Runge_Kut(N, X, Y0, Y, H); Y0 := Y;
PutPixel(Abs(Trunc(Y0[3]*500)), GetMaxY-Abs(Trunc(Y0[4]*500)), L) ;
End;
Bl := Bl * 10; L := L + 1
End;
OutTextXY(10, 50, 'для продолжения нажмите любую клавишу');
Repeat Until KeyPressed; CloseGraph
End.
Приведем пример. Рассмотрим полет чугунного ядра радиуса R=0,07 м, выпущенного с начальной скоростью v0
= 60 м/с под углом ? = 45° к поверхности Земли. Определим, какое расстояние пролетит ядро, на какую максимальную высоту оно поднимется, а также проследим, как изменяется скорость полета со временем. Будем решать обезразмеренные уравнения, чтобы сократить число параметров. Вычислим значения параметров а и b, после чего решим систему дифференциальных уравнений. Учтем, что плотность чугуна ?чуг = 7800 кг/м3.
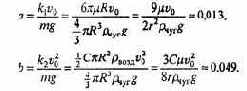
Расчеты повторялись, сначала с шагом 0,1, затем - вдвое меньшим и т.д. (хорошо известный эмпирический метод контроля точности при пошаговом интегрировании дифференциальных уравнений), пока не был получен приемлемый шаг, при котором достигается точность 10-3. Ясно, что расчеты надо проводить до тех пор, пока ядро не достигнет земли, т.е. пока Y не станет равным 0. Результаты моделирования - на рис. 7.9. В рассмотренном выше примере сопротивление среды оказывает незначительное влияние на движение тела. Проведем сравнение движения одного и того же тела без учета сопротивления среды и с его учетом, если среда достаточно вязкая (рис. 7.10).
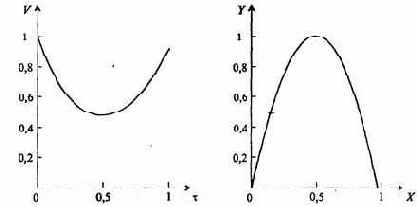
Рис. 7.9. Графики зависимости V(?) и Y(X) при решении задачи о полете ядра.
Безразмерное значение скорости V получается по формуле

Конечное значение скорости V < 1 вследствие сопротивления воздуха.
Траектория движения не является параболой по той же причине
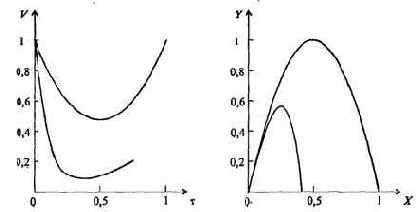
Рис. 7.10. Графики зависимости V(?) и Y(X) при решении задачи о полете тела, брошенного под углом к горизонту, без учета сопротивления воздуха (скорость изменяется от 1 и вновь достигает значения 1; траектория - парабола) и с учетом сопротивления воздуха (конечная скорость меньше 1, и траектория - далеко не парабола) (а = 1, b
= 1)
С помощью приведенной выше программы можно провести полное исследование модели в широком диапазоне значений параметров и составить качественное представление об их влиянии на изучаемое движение. Некоторые результаты иллюстрируются рис. 7.11,7.12.
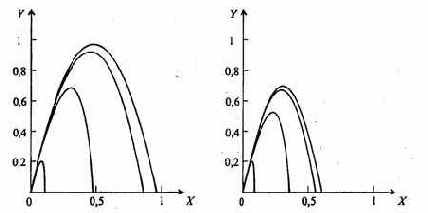
Рис. 7.11. Влияние параметра а на движение тела, брошенного под углом к горизонту, при b = 0,1 (слева) и при b = 1 (справа); ? =
?/4 (а = 0,01; 0,1; 1; 10; кривые на рисунках соответственно располагаются справа налево)
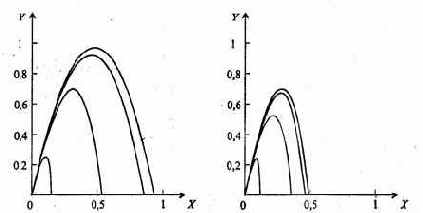
Рис. 7.12. Влияние параметра b на движение тела, брошенного под углом к горизонту, при a = 0,1 (слева) и при а = 1 (справа); ? = ?/4 (b = 0,01; 0,1; 1; 10; кривые на рисунках соответственно располагаются справа налево)