Основы объектно-ориентированного программирования
Компоненты
Пример использует представление точки в двумерной графической системе:
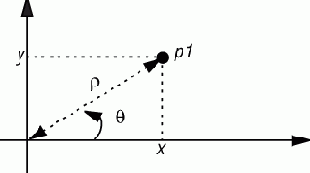
Рис. 7.1. Точка и ее координаты
Для определения типа POINT как абстрактного типа данных потребуется четыре функции-запроса: x, y, ?, ?. (В текстах подпрограмм для двух последних функций будут использоваться имена rho и theta). Функция x возвращает абсциссу точки (горизонтальную координату), y - ординату (вертикальную координату), ? - расстояние от начала координат, ? - полярный угол, отсчитываемый от горизонтальной оси. Значения x и y являются декартовыми, а ? и ? - полярными координатами точки. Другой полезной функцией является distance, возвращающая расстояние между двумя точками.
Далее спецификация АТД будет содержать такие команды, как translate (перемещение точки на заданное расстояние по горизонтали и вертикали), rotate (поворот на определенный угол вокруг начала координат) и scale (уменьшение или увеличение расстояния до начала координат в заданное число раз).
Нетрудно написать полную спецификацию АТД, включающую указанные функции и некоторые ассоциированные аксиомы. Далее в качестве примера приведены две из перечисленных функций:
x: POINT


и одна из аксиом:
x (translate (p1, a, b)) = x (p1) + a
утверждающая, что для произвольной точки p1 и действительных значений a и b при трансляции точки на <a, b> абсцисса увеличивается на a.
Читатель, если пожелает, может самостоятельно завершить спецификацию АТД. В дальнейшей дискуссии подразумевается, что вы понимаете, как устроен данный АТД, вне зависимости от того, написали ли вы его полную формализацию или нет. Сосредоточим внимание на реализации АТД - классе.