Основы объектно-ориентированного программирования
Ингредиенты доказательства корректности цикла
Простой пример вычисления максимума массива иллюстрирует общую схему циклических вычислений, применимую ко многим ситуациям. Вы определяете, что решением некоторой проблемы является элемент, принадлежащий n-мерной поверхности POST. В некоторых случаях POST может содержать ровно один элемент - решение, но обычно может быть более чем одно приемлемое решение проблемы. Циклы полезны, когда нет прямого способа достичь решения "одним выстрелом". Но у вас есть непрямая стратегия, вы можете, например, прицелиться и попасть в m-мерную поверхность INV, включающую POST (для m>n). Инвариантом является то, что поверхность попадания все время содержит POST. Итерация за итерацией приближаемся к POST, сохраняя истинность INV. Следующий рисунок иллюстрирует этот процесс:
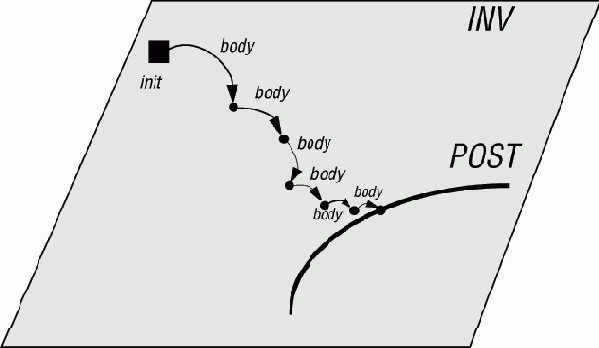
Рис. 11.8. Вычисление цикла (из [М 1990])
Вычисление цикла имеет следующие ингредиенты:
- Цель post, определяемую как свойство, выполняемое в любом допустимом заключительном состоянии. Пример: "Result является максимумом массива". На рисунке цель post представлена множеством состояний POST.
- Инвариант цикла inv, являющийся обобщением цели, так что можно говорить, что цель - это частный случай инварианта. Пример: "Result является максимумом текущей нарезки массива". Инвариант цикла поиска цели, изображенный на рисунке: "Каждая точка лежит на поверхности, содержащей POST.
- Точку инициализации init, о которой известно, что она должна быть в INV, другими словами должна обеспечить выполнение инварианта.
- Преобразование body, начинающееся в INV, но не в POST, вырабатывающее точку более близкую к POST, но все еще остающуюся в INV. Тело цикла функции maxarray является примером подобного преобразования.
- Верхняя граница числа применений body, необходимого для перевода точки из INV в POST. Как будет пояснено ниже, этот параметр необходим для определения варианта.
Последовательные приближения один из главных инструментов численного анализа. Но там эта идея понимается шире. Важная разница состоит в том, что в чистой математике допускаются бесконечные вычисления, последовательность может иметь предел, даже если он не достигается конечным числом приближений.