MathCAD 7.0
Функции создания векторов m различными законами распределения
Функции создания векторов m различными законами распределения
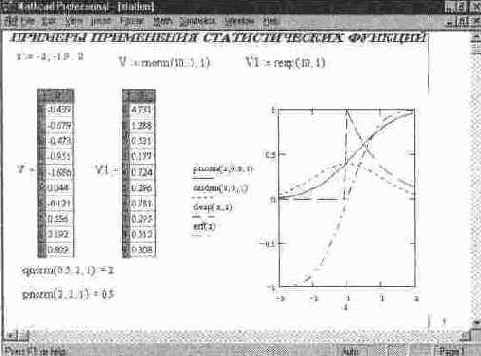
Последняя группа статистических функций служит для создания векторов с определенными законами распределения значений их элементов:
Ф rbeta(m, s1, s2) — бетта-распределение;
rbinom(m, n, p) — биномиальное распределение;
Ф rcauchy(m, /, s) — распределение Коши;
rchisq(m, d) — Хи-квадрат-распределение;
Ф rexp(m, r) — экспоненциальное распределение, rF(m, d1, d2) — распределение Фишера;
Ф rgamma(m, s) — гамма-распределение;
Ф rgeom(m, p) — геометрическое распределение;
Ф rlnorm(m, /л, сг) — логарифмическое нормальное распределение;
Ф rlogis(m, /, s) — последовательное распределение;
Ф mbinom(m, n, p) — негативное биномиальное распределение;
morm(m, m, о) — нормальное распределение;
rpois(m, Я) — распределение Пуассона;
rt(m, d) — распределение Стьюдента;
rumf(m, а, b) — равномерное распределение;
Ф rweibull(m, s) — распределение Вейбулла.