MathCAD 7.0
Полиномиальная регрессия
Рис. 11.25 Полиномиальная регрессия
На практике не рекомендуется делать степень аппроксимирующего поли нома выше четвертой — шестой, поскольку погрешности реализации регрессии сильно возрастают
Функция regress создает единственный приближающий полином, коэффициенты которого вычисляются по всей совокупности заданных точек, т е глобально Иногда полезна другая функция полиномиальной регрессии, дающая локальные приближения отрезками полиномов второй степени, — loess(VX, VY, span). Эта функция возвращает используемый функцией interp(VS,VX,VY,x) вектор VS, дающий наилучшее приближение данных (с координатами точек в векторах VX и VY) отрезками полиномов второй степени Аргумент span>0 указывает размер локальной области приближаемых данных (рекомендуемое начальное значение — 0,75) Чем больше span, тем сильнее сказывается сглаживание данных При больших span эта функция приближается к regress(VX,VY,2)
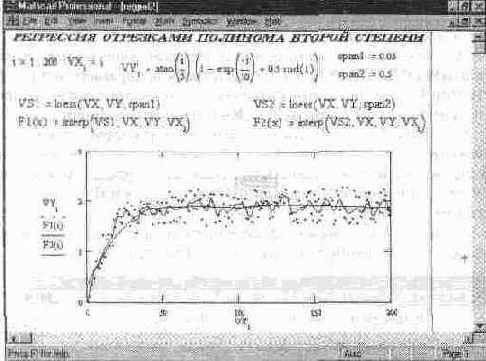
На рис 11 26 показан пример приближения сложной функции со случайным разбросом ее ординат с помощью совокупности отрезков полиномов вто рой степени (функция loess) для двух значений параметра span
На рис 11 26 нетрудно заметить, что при малом значении span, равном 0 05, отслеживаются характерные случайные колебания значений функции, тогда как уже при span=0,5 кривая регрессии становится практически гладкой К сожалению, из-за отсутствия простого описания аппроксимирующей