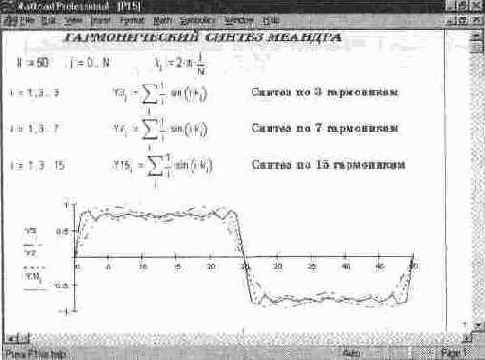
Гармонический синтез меандра

Одним из фундаментальных положений математики, ранее казавшимся абст рактным а затем нашедшим широчайшее практическое применение, является возможность описания любой периодической функции, имеющей конечное число разрывов и непрерывность производных между ними, с помощью три гонометрического ряда Фурье [29, 30]

где k — порядковый номер гармоники, f1 — частота колебания Этот ряд со держит бесконечное число косинусных и синусных составляющих — гармо ник, причем амплитуды этих составляющих а^ и Ь^ являются коэффициента ми Фурье, определяемыми приводимыми несколько позднее интегральными выражениями

Приведенный ряд содержит бесконечное число членов и при таком пред ставлении оказывается бесполезным, поскольку время вычисления в этом случае также равно бесконечности К счастью, амплитуды гармоник для ре альных зависимостей y (t) довольно быстро уменьшаются по мере роста номеpa гармоники k. Поэтому на практике обычно приходится иметь дело с ограниченными по числу гармоник рядами Фурье.

Помимо упомянутой формы ряд Фурье можно представить в виде:

где амплитуда гармоник М^ и их фаза (р^ определяются выражениями:

Преимущество ряда в этой форме в том, что для вычисления каждого члена ряда нужно лишь один раз обращаться к довольно медленному вычислению тригонометрической функции. В дальнейшем будут приведены формулы, позволяющие вычислять коэффициенты Фурье (либо амплитуды и фазы гармоник) для любой функции y (t). Это является задачей спектрального анализа. Здесь же мы рассмотрим обратную задачу — синтеза зависимости y (t) путем вычисления ряда Фурье с ограниченным числом членов.

Теория спектрального анализа и синтеза хорошо развита, и для многих зависимостей y (t) заведомо известны значения коэффициентов Фурье или законы изменения (с частотой или номером гармоники) амплитуд и фаз гармоник. Это позволяет синтезировать наиболее распространенные зависимости y (t).

Содержание раздела

---

---