MathCAD 7.0
Решение дифференциального уравнения первого порядка методом Рунге — Кутта
Решение дифференциального уравнения первого порядка методом Рунге — Кутта
Решение дифференциальных уравнений широко применяется в практике научно-технических расчетов Это связано с тем, что дифференциальные уравнения (и системы из них) описывают поведение различных объектов в динамике, например переходные процессы в электронных схемах или работу часового маятника Линейные дифференциальные уравнения имеют решения в виде специальных функций (скажем, функций Бесселя) Однако многие физические системы нелинейны и описываются нелинейными дифференциальными уравнениями, не имеющими аналитического решения. В этом случае приходится использовать численные методы решения дифференциальных уравнений.
Версия MathCAD 7. 0 PRO содержит мощные средства для реализации численных методов решения дифференциальных уравнений. Поэтому может возникнуть вопрос: а нужно ли создавать свои документы для реализации таких методов? Ответ на него не однозначен. Если ваша цель — решение конкретной задачи, то проще воспользоваться готовыми функциями MathCAD. Они были описаны выше. Однако нередко педагоги и специалисты без должных оснований говорят о трудности реализации в системе MathCAD обычных численных методов. Это неверно! Реализация таких методов в системе MathCAD легка и наглядна. Более того, она позволяет вмешиваться в алгоритмическую реализацию методов решения, что способствует созданию новых или улучшенных методов решения дифференциальных уравнений, ориентированных на решение интересующих пользователя задач.
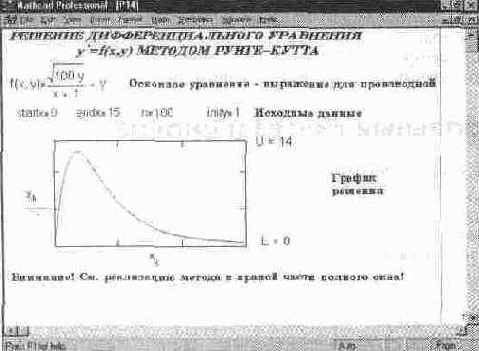
Здесь мы остановимся на реализации решения дифференциального уравнения i/=f (x, y) хорошо известным методом Рунге — Кутта. Пусть h — шаг приращения переменной х, i — индекс, имеющий значения от 1 до N (N — число интервалов решения с шагом h). Метод Рунге — Кутта четвертого порядка дает погрешность решения порядка h (4, что удовлетворяет самым при-щрчивым требованиям к точности численных методов. Он неоднократно подробно описывался в [6, 8, 14]. Его реализация показана на рис. 14. 16.