10.6. Другие спецфункции (Special)

Приведем перечень остальных спецфункций, которые рассчитываются Mathcad встроенным образом. Действие некоторых функций иллюстрируется листингом 10.8, а некоторые полиномы — графиками на рис. 10.11—10.13.

• erf (z) — функция ошибок (см. разд. "Нормальное (Гауссово) распределение" гл. 14)
• erfc(z)=1-erf(z);




• z — скаляр.
• fhyper(а,b,с,х) —Гауссова гипергеометрическая функция;
• mhyper(a,b,x) — конфлюэнтная гипергеометрическая функция;
• а, b, с — параметры;
• х — действительный скаляр, -1<х<1.
• Gamma (z) — гамма-функция Эйлера;
• z — скаляр, |z|<1.
• Gamma (а, х) — неполная гамма-функция порядка а;
• х — действительный положительный скаляр.

Гамма-функция в документе Mathcad отображается греческой буквой Г (листинг 10.8).

• нег(n,х) — полином Эрмита порядка n с аргументом х (рис. 10.10);
• n — порядок (неотрицательное целое число);
• х — скаляр.

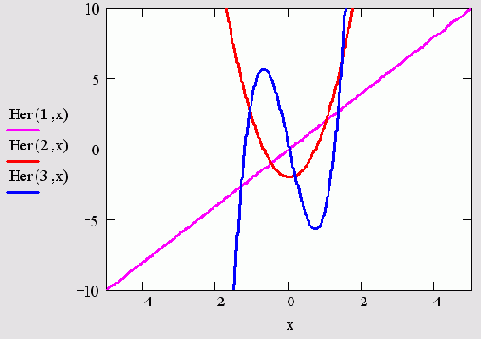
Рис. 10.10. Полиномы Эрмита

• ibeta(a,x,y) — неполная бета-функция для х и у с параметром а;
• а — действительный скаляр, 0<a<i;
• х,у — действительные скаляры, х>0, у>0.
• Jac (n, а, b, х) — полином Якоби степени n в точке х с параметрами а и b;
• Lag(n,x) — полином Лагерра степени n в точке х (рис. 10.11);

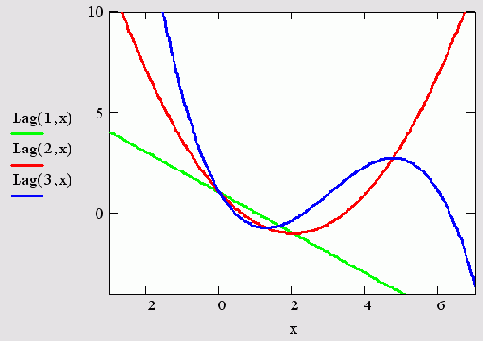
Рис. 10.11. Полиномы Лаггера

• Leg(n,x) — полином Лежандра степени п в точке х (рис. 10.12);
• n — порядок (неотрицательное целое число);
• х - действительный скаляр;
• а,b — действительные скаляры, а>-1, b>-1.
• Tcheb(n,x) — полином Чебышева первого рода степени n в точке х (рис. 10.13);
• Ucheb(n,x) — полином Чебышева второго рода степени n в точке х (рис. 10.13);
• n — порядок (неотрицательное целое число);
• х — действительный скаляр.

Листинг 10.8. Примеры вычисления некоторых спецфункций

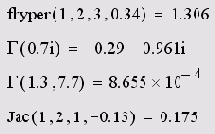
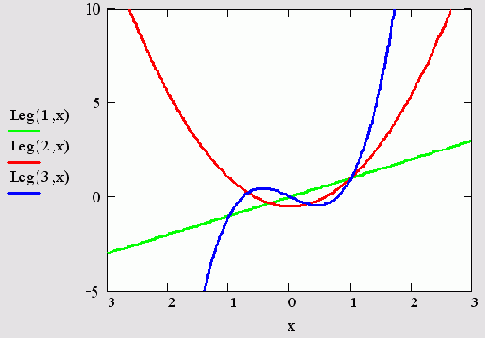
Рис. 10.12. Полиномы Лежандра

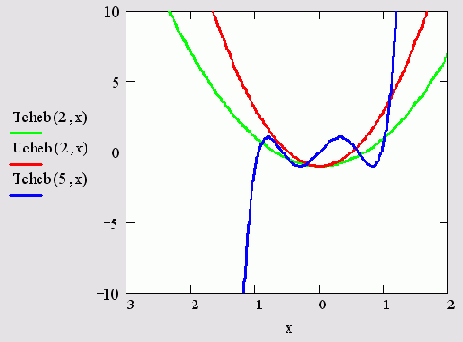
Рис. 10.13. Полиномы Чебышева

Содержание раздела

---

---