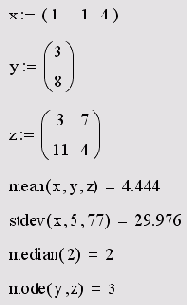Математический редактор MathCAD
14.2.7. Действие статистических функций на матрицы
Все рассмотренные примеры работы статистических функций относились к векторам, элементы которых были случайными числами. Но точно так же все эти функции применяются и по отношению к выборкам случайных данных, сгруппированных в матрицы. При этом статистические характеристики рассчитываются для совокупности всех элементов матрицы, без разделения ее на строки и столбцы. Например, если матрица имеет размерность MXN, то и объем выборки будет равен M-N.
Соответствующий пример вычисления среднего значения приведен в листинге 14.16. В его первой строке определяется матрица данных х размера 4x2. Действие встроенной функции mean матричного аргумента (последняя строка листинга) иллюстрируется явным суммированием элементов матрицы х (предпоследняя строка). Действие прочих встроенных функций на матрицы совершенно аналогично действию их на векторы (листинг 14.17).
Листинг 14.16. Вычисление среднего значения элементов матрицы
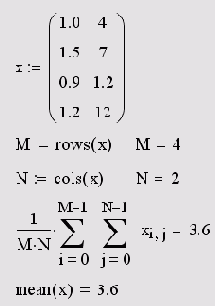
Листинг 14.17. Действие различных статических функций на матрицу
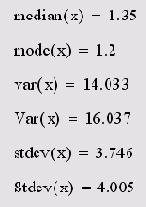
Некоторые статистические функции (например, вычисления ковариации) имеют два аргумента. Они также могут быть матрицами, но, в соответствии со смыслом функции, должны иметь одинаковую размерность.
Большинству статистических функций позволяется иметь в качестве аргументов даже не одну матрицу, а любое количество матриц, векторов и скаляров. Числовые характеристики будут рассчитаны для всей совокупности значений аргументов функции. Соответствующий пример приведен в листинге 14.18.
Листинг 14.18. Статические функции нескольких аргументов