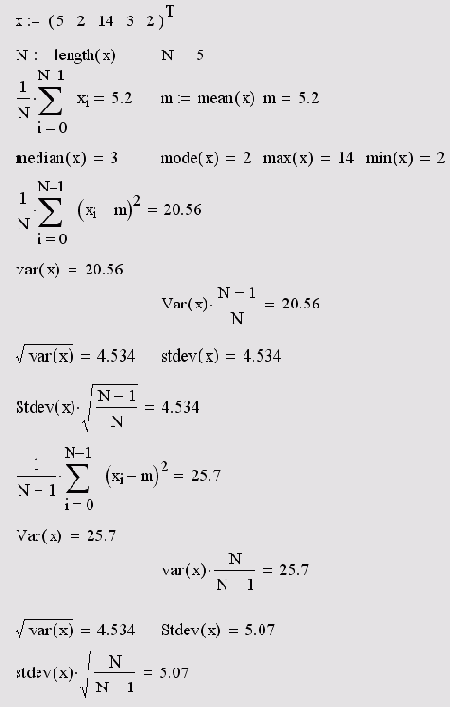Математический редактор MathCAD
14.2.2. Среднее значение и дисперсия
В Mathcad 11 имеется ряд встроенных функций для расчетов числовых статистических характеристик рядов случайных данных.
- mean(x) —выборочное среднее значение;
- median (х) — выборочная медиана (median) — значение аргумента, которое делит гистограмму плотности вероятностей на две равные части;
- var(x) — выборочная дисперсия (variance);
- stdev(x) — среднеквадратичное (или "стандартное") отклонение (standard deviation);
- max(x), mm (x) — максимальное и минимальное значения выборки;
- mode(x) — наиболее часто встречающееся значение выборки;
- var (x) ,stdev(x) — выборочная дисперсия и среднеквадратичное отклонение в другой нормировке;
- х — вектор (или матрица) с выборкой случайных данных.
Пример использования первых четырех функций приведен в листинге 14.10.
Листинг 14.10. Расчет числовых характеристик случайного вектора
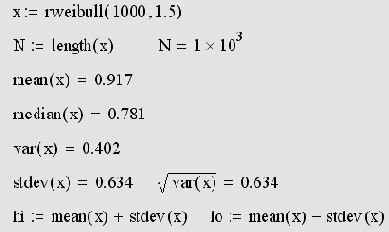
На рис. 14.12 приведена гистограмма выборки случайных чисел, распределенных согласно закону Вейбулла. Пунктирные вертикальные прямые, показанные на графике, рассчитаны в последней строке листинга и обозначают стандартное отклонение от среднего значения. Гистограмма получена с помощью листинга 14.8, рассмотренного в предыдущем разделе. Обратите внимание, что поскольку распределение Вейбулла, в отличие, например, от Гауссова, несимметричное, то медиана не совпадает со средним значением.
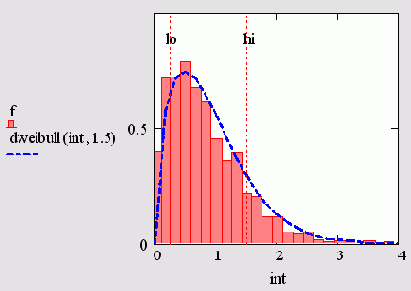
Рис. 14.12. Гистограмма распределения Вейбулла (листинг 14.10)
Определение статистических характеристик случайных величин приведено в листинге 14.11 на еще одном примере обработки выборки малого объема (по пяти данным). В том же листинге иллюстрируется применение еще двух функций, которые имеют смысл дисперсии и стандартного отклонения в несколько другой нормировке. Сравнивая различные выражения, Вы без труда освоите связь между встроенными функциями.
Осторожно относитесь к написанию первой литеры в этих функциях, особенно при обработке малых выборок (листинг 14.11).
Листинг 14.11. Копределению статических характеристик