Математический редактор MathCAD
15.1.5. Многомерная интерполяция
Двумерная сплайн-интерполяция приводит к построению поверхности z(x,y), проходящей через массив точек, описывающий сетку на координатной плоскости (х,у). Поверхность создается участками двумерных кубических сплайнов, являющихся функциями (х,у) и имеющих непрерывные первые и вторые производные по обеим координатам.
Многомерная интерполяция строится с помощью тех же встроенных функций, что и одномерная (см. разд. 15.1.2), но имеет в качестве аргументов не векторы, а соответствующие матрицы. Существует одно важное ограничение, связанное с возможностью интерполяции только квадратных NXN массивов данных.
- interp(s,x,z,v) — скалярная функция, аппроксимирующая данные выборки двумерного поля по координатам х и у кубическими сплайнами;
- s — вектор вторых производных, созданный одной из сопутствующих функций cspline, pspline или lspline;
- х — матрица размерности Nx2, определяющая диагональ сетки значений аргумента (элементы обоих столбцов соответствуют меткам х и у и расположены в порядке возрастания);
- z — матрица действительных данных размерности NXN;
- v — вектор из двух элементов, содержащий значения аргументов х и у, для которых вычисляется интерполяция.
Вспомогательные функции построения вторых производных имеют те же матричные аргументы, что и interp: Ispline (X,Y), pspline (X, У), cspline(X,Y).
Пример исходных данных приведен на рис. 15.10 в виде графика линий уровня, программная реализация двумерной интерполяции показана в листинге 15.6, а ее результат — на рис. 15.11.
Листинг 15.6. Двумерная интерполяция

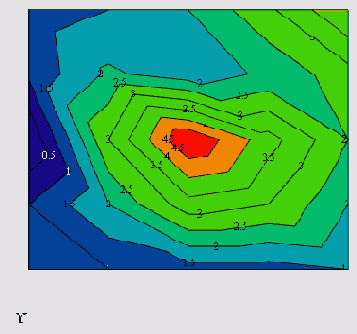
Рис. 15.10. Исходное двумерное поле данных (листинг 15.6)
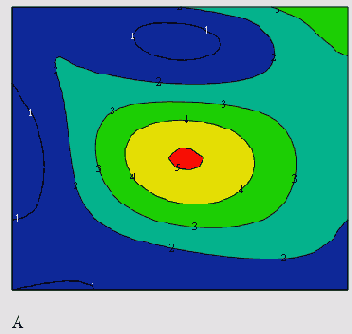
Рис. 15.11. Результат двумерной интерполяции (листинг 15.6)