Математический редактор MathCAD
15.2.1. Линейная регрессия
Самый простой и наиболее часто используемый вид регрессии — линейная. Приближение данных (xi, yi) осуществляется линейной функцией у(х)=b+ах. На координатной плоскости (х,у) линейная функция, как известно, представляется прямой линией (рис. 15.12). Еще линейную регрессию часто называют методом наименьших квадратов, поскольку коэффициенты а и ь вычисляются из условия минимизации суммы квадратов ошибок |b+axi-yi|.
Чаще всего такое же условие ставится и в других задачах регрессии, т. е. приближения массива данных (хi,уi) другими зависимостями у(х). Исключение рассмотрено в листинге 15.9.
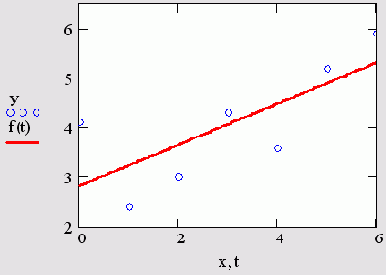
Рис. 15.12. Линейная регрессия (листинг 15.7 или 15.8)
Для расчета линейной регрессии в Mathcad имеются два дублирующих друг друга способа. Правила их применения представлены в листингах 15.7 и 15.8. Результат обоих листингов получается одинаковым (рис. 15.12).
- line(x,y) — вектор из двух элементов (b,а) коэффициентов линейной регрессии ь+а-х;
- intercept (x,y) — коэффициент b линейной рефессии;
- slope(x,y) — коэффициент а линейной рефессии;
- х — вектор действительных данных аргумента;
- у — вектор действительных данных значений того же размера.
Листинг 15.7. Линейная регрессия
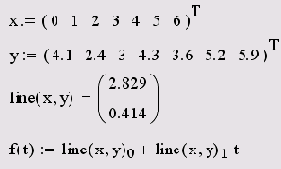
Листинг 15.8. Другая форма записи линейной регрессии

В Mathcad имеется альтернативный алгоритм, реализующий не минимизацию суммы квадратов ошибок, а медиан-медианную линейную рефессию для расчета коэффициентов а и ь (листинг 15.9).
- medfit(x,y) — вектор из двух элементов (b,а) коэффициентов линейной медиан-медианной рефессии b+ах;
- х,у — векторы действительных данных одинакового размера.
Листинг 15.9. Построение линейной регрессии двумя разными иетодами (продолжение листинга 15.7)
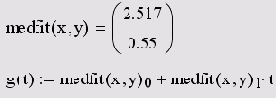
Различие результатов среднеквадратичной и медиан-медианной рефессии иллюстрируется рис. 15.13.
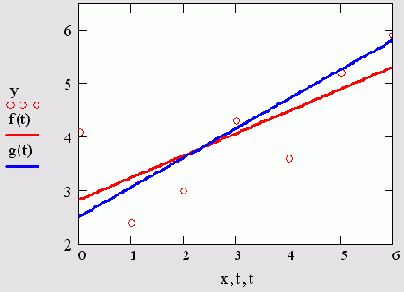
Рис. 15.13. Линейная регрессия по методу наименьших квадратов и методу медиан (листинги 15.7 и 15.9)