Математический редактор MathCAD
5.2.5. Коэффициенты полинома (Polynomial Coefficients)
Если выражение является полиномом относительно некоторой переменной х, заданным не в обычном виде а0+а1х+а2х2+..., а как произведение других, более простых полиномов, то коэффициенты а0+а1+а2 легко определяются символьным процессором Mathcad. Коэффициенты сами могут быть функциями (подчас, довольно сложными) других переменных.
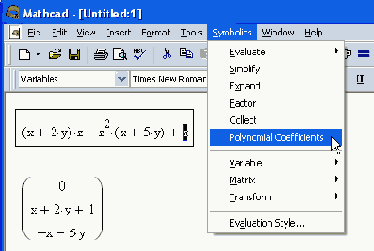
Рис. 5.10. Вычисление коэффициентов полинома
Чтобы вычислить полиномиальные коэффициенты в выражении при помощи меню (рис. 5 10):
- Введите выражение.
- Выделите в нем имя переменной или выражение, для которого требуется рассчитать полиномиальные коэффициенты (в примере на рис. 5.10 это переменная z).
- Выполните команду Symbolic / Polynomial Coefficients (Символика / Коэффициенты полинома).
В результате под выражением появится вектор, состоящий из полиномиальных коэффициентов. Первым элементом вектора является свободный член а0, вторым — а1, и т. д.
Конкретная задача, требующая вычисления полиномиальных коэффициентов, приведена в разделе, посвященном численному отделению корней полинома (см. разд. "Корни полинома" гл. 8).
Чтобы вычислить полиномиальные коэффициенты с помощью оператора символьного вывода:
- Введите выражение.
- Нажмите кнопку Coeffs на панели Symbolic (Символика).
- Введите в местозаполнитель после вставленного ключевого слова coeffs аргумент полинома.
- Введите оператор символьного вывода ->
- Нажмите клавишу <Enter>.
Примеры вычисления коэффициентов полинома приведены в листингах 5.7 и 5.8. Листинг 5.7 показывает расчет коэффициентов для разных аргументов. Последний листинг демонстрирует возможность определения коэффи-щентов не только для отдельных переменных, но для более сложных выражений, входящих в рассматриваемую формулу в качестве составной части.
Листинг 5.7. Вычисление коэффициентов полинома
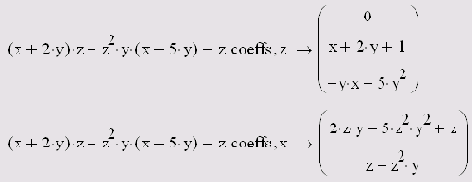
Листинг 5.8. Вычисление полиноминальных коэффициентов для простой переменной и выражения