Математический редактор MathCAD
8.7. Символьное решение уравнений
Некоторые уравнения можно решить точно с помощью символьного процессора Mathcad. Делается это очень похоже на численное решение уравнений с применением вычислительного блока. Присваивать неизвестным начальные значения нет необходимости. Листинги 8.16 и 8.17 демонстрируют символьное решение уравнения с одним неизвестным и системы двух уравнений с двумя неизвестными соответственно.
Листинг 8.16. Символьное решение алгебраического уравнения с одним неизвестным
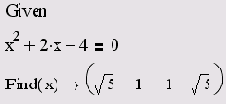
Листинг 8.17. Символьное решение системы алгебраических уравнений
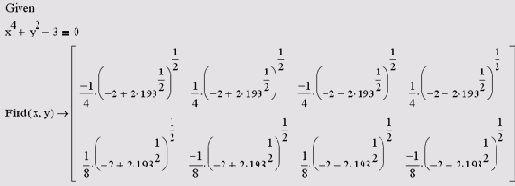
Как видно, вместо знака равенства после функции Find в листингах следует знак символьных вычислений, который можно ввести с панели Symbolic (Символика) или, нажав клавиши <Ctrl>+<.>. He забывайте, что сами уравнения должны иметь вид логических выражений, т. е. знаки равенства нужно вводить с помощью панели Booleans (Булевы операторы). Обратите внимание, что в листинге 8.17 вычислены как два первых действительных корня, которые мы уже находили численным методом (см. разд. 8.3), так и два других мнимых корня. Эти два последних корня чисто мнимые, т. к. множитель, входящий в них.
С помощью символьного процессора решить уравнение с одним неизвестным можно и по-другому:
- Введите уравнение, пользуясь панелью Booleans (Булевы операторы) или нажав клавиши <Ctrl>+<> для получения логического знака равенства, например х2+2(х-4)=0.
- Щелчком мыши выберите переменную, относительно которой Вы собираетесь решить уравнение.
- Выберите в меню Symbolics (Символика) пункт Variable / Solve (Переменная / Решить).
После строки с уравнением появится строка с решением или сообщение о невозможности символьного решения этого уравнения.
В данном примере после осуществления описанных действий появляется вектор, состоящий из двух корней уравнения
Символьные вычисления могут производиться и над уравнениями, в которые, помимо неизвестных, входят различные параметры. В листинге 8.18 приведен пример решения уравнения четвертой степени с параметром а. Как видите, результат получен в аналитической форме.
Листинг 8.18. Символьное решение уравнения, зависящего от параметра
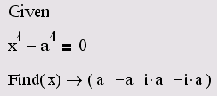
В следующем разделе мы рассмотрим более подробно, как с помощью Mathcad можно численными методами решать подобные задачи.