Математический редактор MathCAD
8.3. Системы уравнений
Рассмотрим решение системы N нелинейных уравнений с M неизвестными
f1(x1, ... ,хм) = 0,
. . . (1)
fn(x1, ... ,хм) = 0,
Здесь f1(x1, ... ,хм) , ..., fn(x1, ... ,хм) — некоторые скалярные функции от скалярных переменных хцх2/ ... /хм и, возможно, от еще каких-либо переменных. Уравнений может быть как больше, так и меньше числа переменных. Заметим, что систему (1) можно формально переписать в виде
f(x)=0, (2)
где х — вектор, составленный из переменных x1,х2, ... ,хм, a f (х) — соответствующая векторная функция.
Для решения систем имеется специальный вычислительный блок, состоящий из трех частей, идущих последовательно друг за другом:
- Given — ключевое слово;
- система, записанная логическими операторами в виде равенств и, возможно, неравенств;
- Find(x1... ,хм) — встроенная функция для решения системы относительно переменных хх,..., хм.
Вставлять логические операторы следует, пользуясь панелью инструментов Boolean (Булевы операторы). Если Вы предпочитаете ввод с клавиатуры, помните, что логический знак равенства вводится сочетанием клавиш <Ctrl>+<=>. Блок Given/Find использует для поиска решения итерационные методы, поэтому, как и для функции root, требуется задать начальные значения для всех х1, ... ,xм. Сделать это необходимо до ключевого слова Given. Значение функции Find есть вектор, составленный из решения пс каждой переменной. Таким образом, число элементов вектора равно число аргументов Find.
В листинге 8.6. приведен пример решения системы двух уравнений.
Листинг 8.6. Решение системы уравнений
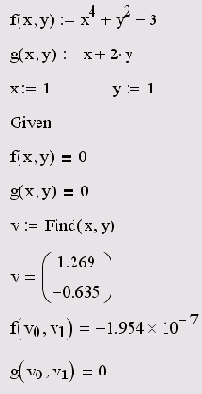
В первых двух строках листинга вводятся функции, которые определяют систему уравнений. Затем переменным х и у, относительно которых она будет решаться, присваиваются начальные значения. После этого следует ключевое слово Given и два логических оператора, выражающих рассматриваемую систему уравнений. Завершает вычислительный блок функция Find, значение которой присваивается вектору v. Следующая строка показывает содержание вектора v, т. е. решение системы. Первый элемент вектора есть первый аргумент функции Find, второй элемент — ее второй аргумент. В последних двух строках осуществлена проверка правильности решения уравнений.
Часто бывает очень полезно проверить точность решения уравнений, вычислив значения образующих их функций в найденных вычислительным процессором корнях, как это сделано в конце листинга 8.6.
Отметим, что уравнения можно определить непосредственно внутри вычислительного блока. Таким образом, можно не определять заранее функции f (x,y) и д(х,у), как это сделано в первых двух строках листинга 8.6, а сразу написать:
Given
х4 + у2 =3
х+ 2 у = 0
Такая форма представляет уравнения в более привычной и наглядной форме, особенно подходящей для документирования работы.
Графическая интерпретация рассмотренной системы представлена на рис. 8.3. Каждое из уравнений показано на плоскости XY графиком. Первое — сплошной кривой, второе — пунктиром. Поскольку второе уравнение линейное, то оно определяет на плоскости XY прямую. Две точки пересечения кривых соответствуют одновременному выполнению обоих уравнений, т. е. искомым действительным корням системы. Как нетрудно убедиться, в листинге найдено только одно из двух решений — находящееся в правой нижней части графика Чтобы отыскать и второе решение, следует повторить вычисления, изменив начальные значения так, чтобы они лежали ближе к другой точке пересечения графиков, например x=-1, y=-1.
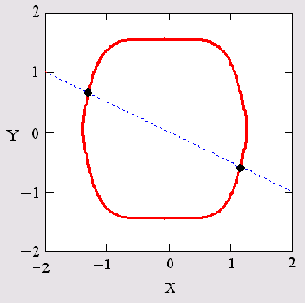
Рис. 8.3. Графическое решение системы двух уравнений
Пока мы рассмотрели пример системы из двух уравнений и таким же числом неизвестных, что встречается наиболее часто. Но число уравнений и неизвестных может и не совпадать. Более того, в вычислительный блок можно добавить дополнительные условия в виде неравенств. Например, введение ограничения на поиск только отрицательных значений х в рассмотренный выше листинг 8.6 приведет к нахождению другого решения, как это показано в листинге 8.7.
Листинг 8.7. Решение системы уравнений и неравенств
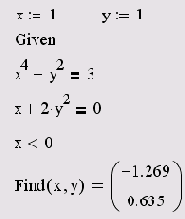
Обратите внимание, что, несмотря на те же начальные значения, что и в листинге 8.6, мы получили в листинге 8.7 другой корень. Это произошло именно благодаря введению дополнительного неравенства, которое определено в блоке Given в предпоследней строке листинга 8.7.
Если предпринять попытку решить несовместную систему, Mathcad выдаст сообщение об ошибке, гласящее, что ни одного решения не найдено, и предложение попробовать поменять начальные значения или значение погрешности.
Вычислительный блок использует константу CTOL в качестве погрешности выполнения уравнений, введенных после ключевого слова Given. Например, если CTOL=0.001, то уравнение х=10 будет считаться выполненным и при х=10.001, и при х=9.999. Другая константа TOL определяет условие прекращения итераций численным алгоритмом (см. разд. 8.4). Значение стоъ может быть задано пользователем так же как и TOL, например, CTOL:=0.01. По умолчанию принято, что CTOL=TOL=0.001, но Вы по желанию можете переопределить их.
Особенную осторожность следует соблюдать при решении систем с числом неизвестных большим, чем число уравнений. Например, можно удалить одно из двух уравнений из рассмотренного нами листинга 8.6, попытавшись решить единственное уравнение g(х,у)=о с двумя неизвестными х и у. В такой постановке задача имеет бесконечное множество корней: для любого х и, соответственно, у=-х/2 условие, определяющее единственное уравнение, выполнено. Однако, даже если корней бесконечно много, численный метод будет производить расчеты только до тех пор, пока логические выражения в вычислительном блоке не будут выполнены (в пределах погрешности). После этого итерации будут остановлены и выдано решение. В результате будет найдена всего одна пара значений (х,у), обнаруженная первой.
О том, как найти все решения рассматриваемой задачи, рассказывается в разд. 8.7.
Вычислительным блоком с функцией Find можно найти и корень уравнения с одним неизвестным. Действие Find в этом случае совершенно аналогично уже рассмотренным в данном разделе примерам. Задача поиска корня рассматривается как решение системы, состоящей из одного уравнения. Единственным отличием будет скалярный, а не векторный тип числа, возвращаемого функцией Find. Пример решения уравнения из предыдущего раздела приведен в листинге 8.8.
Листинг 8.8. Поиск корня уравнения с одним неизвестным с помощью функции Find
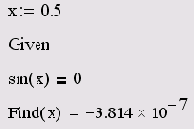
В чем же отличие приведенного решения от листинга 8.1 с функцией root? Оно состоит в том, что одна и та же задача решена различными численными методами. В данном случае выбор метода не влияет на окончательный результат, но бывают ситуации, когда применение того или иного метода имеет решающее значение.