Математические задачи в пакете MathCAD 12
Глава 3.2.1. Дифференцирование в точке
Для того чтобы численно продифференцировать функцию f (х) в некоторой точке, следует использовать оператор численного вывода (вместо символьного):
1. Определите точку х, в которой будет вычислена производная, например,
х:=1.
2. Введите оператор дифференцирования и обычным образом введите имена функции и аргумента в местозаполнители (см. рис. 3.1).
3. Введите оператор = численного вывода результата.
Пример дифференцирования функции f (x)=sin(x) ln(x) приведен в листинге 3.5.
Листинг 3.5. Численное дифференцирование функции в точке
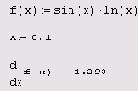
ВНИМАНИЕ!
Не забывайте предварительно определять точку, в которой производится численное дифференцирование, как это сделано во второй строке листинга 3.5. Иначе будет выдано сообщение об ошибке, показанное на рис. 3:4, гласящее, что переменная или функция, входящая в выражение, ранее не определена. Между тем, символьное дифференцирование (см. разд. 3.1) не требует обязательного явного задания точки дифференцирования. В этом случае вместо значения производной (числа или числового выражения) будет выдана аналитическая зависимость (см. листинг 3.1).

Рис. 3.4. Ошибка в применении оператора дифференцирования (не задан аргумент)
ПРИМЕЧАНИЕ
В Mathcad 11 и выше для ускорения и повышения точности численного дифференцирования функций, заданных аналитически, автоматически задействуется символьный процессор. Сначала предпринимается попытка отыскать производные, входящие в выражение, аналитически, а уже затем, если она оказывается неудачной, включается в работу численный метод.