Математические задачи в пакете MathCAD 12
Глава 3.4.1. Частные производные
Примеры отыскания частных производных функции двух переменных приведены в листингах 3.11 и 3.12. В первой строке обоих листингов определяется сама функция, а в последующих (символьным или численным образом) рассчитываются ее производные по обеим переменным —
х и k. Чтобы определить частную производную в точке, необходимо предварительно задать значения всех аргументов, что и сделано в следующих строках листинга 3.12. Обратите внимание, что для символьного поиска производной функции нет необходимости задавать значения всех ее аргументов (третья строка листинга 3.12), а вот для численного дифференцирования (последняя строка листинга) должны быть предварительно определены все аргументы функции, иначе вместо результата появится сообщение об ошибке.
Листинг 3.11. Аналитическое вычисление частных производных
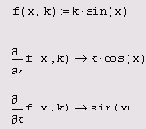
Листинг 3.12.
Символьное и численное вычисления частных производных в точке
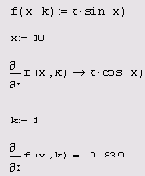
Частные производные высших порядков рассчитываются точно так же, как и обычные
производные высших порядков (см. разд. 3.3). Листинг 3.13 иллюстрирует расчет вторых производных функции по переменным х и у, а также смешанной производной.
Листинг 3.13. Вычисление второй частной производной
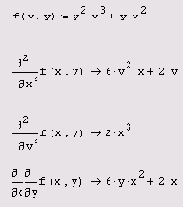
Возможно, вы обратили внимание, что во всех трех листингах 3.11—3.13 оператор дифференцирования записан в традиционной форме частной производной (с округлыми символами дифференциала). Запись оператора не влияет на вычисления, а служит лишь более привычной формой представления расчетов.
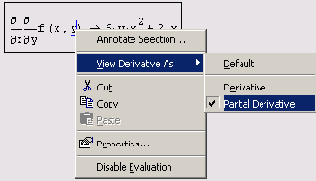
Рис. 3.8. Изменение вида оператора дифференцирования
Для того чтобы изменить вид оператора дифференцирования на представление частной производной, следует:
1. Вызвать контекстное меню из области оператора дифференцирования нажатием правой кнопки мыши.
2. Выбрать в контекстном меню верхний пункт View Derivative As (Показывать производную как).
3. В появившемся подменю (рис. 3.8) выбрать пункт Partial Derivative (Частная производная).
Чтобы вернуть вид производной, принятый по умолчанию, выберите в подменю пункт
Default (По умолчанию) либо, для представления ее в обычном виде, — Derivative (Производная).