Глава 4.1.3.О традиционных алгоритмах интегрирования

Прежде чем перейти к изложению метода численного интегрирования, реализованного в Mathcad, скажем несколько слов об основных принципах численного интегрирования. Исходя из геометрического смысла определенного интеграла функции f (х) как площади фигуры, образованной графиком этой функции и осью х, можно предложить самый простой способ интегрирования "хорошей" функции — применить формулу прямоугольников. С ее помощью площадь упомянутой искомой фигуры подсчитывается как сумма элементарных прямоугольников, множеством которых заменяется подынтегральная функция f (х).

Иллюстрация метода прямоугольников приведена на рис. 4.4. Для подсчета интеграла i интервал интегрирования [а,b] разбивается на N отрезков. На. каждом i-м отрезке f (х) заменяется прямоугольником с шириной h и высотой f (x_i). Площадь каждого из этих элементарных прямоугольников составляет

hf (x_i), а их сумма s может считаться приближением к искомому интегралу I. Несложно показать, что при N->~ множество элементарных прямоугольников стремится к искомой фигуре, образованной подынтегральной функцией, а значение S->I, причем погрешность (отличие s от точного значения i) составляет o(h²).

Можно воспринимать смысл алгоритма прямоугольников в замене исходной подынтегральной функции другой, близкой к ней (в данном случае, кусочно-непрерывной) функцией, интеграл от которой легко подсчитать аналитически. Принцип более точных методов интегрирования как раз и состоит в интерполяции подынтегральной функции f (х) некоторой близкой зависимостью у(х) и расчете интеграла уже от этой функции. Важно, чтобы при этом, во-первых, интеграл от у(х) мог быть точно рассчитан аналитическими методами; и, во-вторых, функция f (х) была бы по возможности ближе к у (х), чтобы уменьшить погрешность.

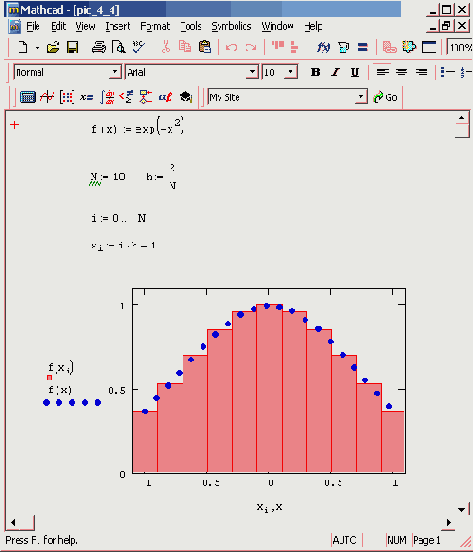
Рис. 4.4. Реализация алгоритма прямоугольников

Очевидно, что наиболее простой алгоритм заключается в интерполяции подынтегральной функции на каждом из N шагов интегрирования f (х) каким-либо полиномом у(х). Известно, что могут быть предложены различные пути построения интерполирующих полиномов, отличающихся, в частности, порядком. Например, полиномы Лагранжа строятся при интерполяции f (х) в n точках на каждом из N элементарных интервалов интегрирования. Семейство классических алгоритмов интегрирования в этом случае называется методами Ньютона—Котеса. Заметим, что при n=1 полиномом является прямая линия, и мы имеем метод трапеций; при n=2 интерполирующим полиномом на каждом шаге интегрирования будет квадратичная парабола, и мы получим алгоритм Симпсона и т. д.

ПРИМЕЧАНИЕ

Дополнительные сведения об алгоритме полиномиальной интерполяции приведены в главе 13.

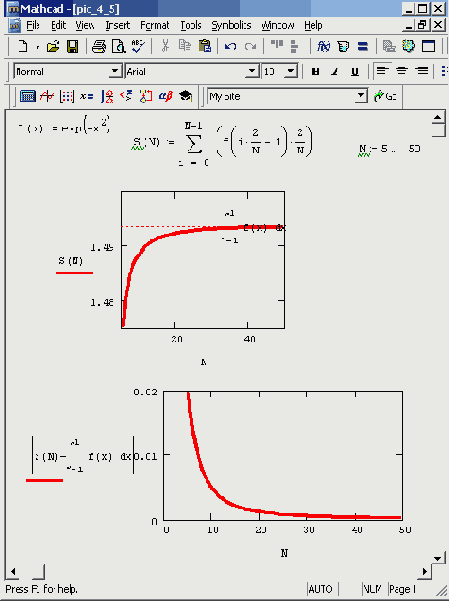
Рис. 4.5. Оценка погрешности алгоритма прямоугольников

Недостатком перечисленных традиционных алгоритмов являются затруднения в количественной оценке погрешности. Аналитические формулы для погрешности включают, помимо множителя ьк, задающего, собственно, порядок аппроксимации метода, сомножитель, характеризующий величину производной (определенного высшего порядка) подынтегральной функции. Оценить ее значение при конкретных расчетах очень сложно, и поэтому, соответственно, сложно вычислить суммарную погрешность алгоритма. В то же время сведения о величине погрешности являются очень важными, и, чаще всего, желательно иметь их количественную оценку, чтобы оптимально выбрать число разбиений интервала интегрирования N.

Для апостериорной оценки погрешности можно, например, применять анализ зависимости s(N), подсчитанной для нескольких значений N (рис. 4.5). Зная, что, с одной стороны, s(N) изменяется по определенному степенному закону N~K, и, с другой, s(N)->i (к точному значению интеграла), можно довольно точно определить погрешность метода. На нижнем графике рис. 4.5 приведена зависимость погрешности от N (правда, в данном случае мы использовали для наглядности графика точное значение интеграла, которое в практических случаях, конечно, неизвестно). Именно с подобной процедурой и связан алгоритм расчета определенных интегралов, использованный в Mathcad, который будет представлен в следующем разделе.

Содержание раздела