Математические задачи в пакете MathCAD 12
Глава 4.4. Интеграл Фурье
Обратимся теперь к характерным проблемам вычислительной математики, связанным с (аналитическим или численным) вычислением интегралов определенного вида. Задачи, о которых мы собираемся рассказать, тесно связаны с алгоритмами обработки данных, поэтому содержание этого раздела будет перекликаться с материалом главы 14 (см. разд. 14.1). Благодаря обширному применению для вычисления таких интегралов разработаны специфические алгоритмы, несравненно более эффективные, чем традиционные (см. разд. 4.1.4), причем некоторые из них имеются в арсенале Mathcad в форме встроенных функций вычислительного процессора и соответствующих операций символьного процессора.
Наиболее широко распространенным интегральным преобразованием является преобразование Фурье, которое представляет функцию f (х) в виде интеграла по гармоническим функциям, называемого интегралом Фурье:
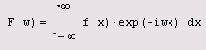
Функция F(CO) называется также преобразованием Фурье, или Фурье-спектром исходной функции f (х). Ее аргумент ш имеет смысл частоты соответствующей гармонической составляющей f (х). Важно отметить, что функция, выражающая преобразование Фурье, комплексна, даже если f(x) является действительной.