Математические задачи в пакете MathCAD 12
Нелинейные алгебраические уравнения
Огромное количество задач вычислительной математики связано с решением нелинейных алгебраических уравнений, а также систем таких уравнений. При этом необходимость решения нелинейных уравнений возникает зачастую на промежуточных шагах, при реализации фрагментов более сложных алгоритмов (к примеру, при расчетах дифференциальных уравнений при помощи разностных схем и т. п.).
Постановка задач выглядит следующим образом. Пусть имеется либо одно алгебраическое уравнение с неизвестным х:
f(x)=0,
(где f(х) — некоторая функция), либо система из N алгебраических уравнений:
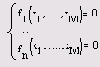
Требуется найти корни, т. е. все значения х (или, в случае системы все м-покомпонентные векторы х), которые переводят уравнение (или, соответственно, систему уравнений) в верное равенство (равенства).
ПРИМЕЧАНИЕ
Решение систем линейных уравнений, у которых все функции имеют вид fi (х)=аi1х1+аi2х2+. . . +ainxN, представляет собой отдельную задачу вычислительной линейной алгебры. Она рассматривается в главе 8.
| Содержание |