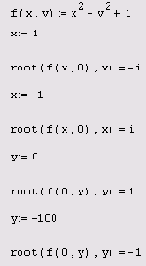Глава 5.2.2. Уравнение с одним неизвестным: функция root

Для решения уравнения с одним неизвестным в Mathcad, помимо вычислительного блока Given/Find, предусмотрена встроенная функция root, которая, в зависимости от типа задачи, может включать либо два, либо четыре аргумента и, соответственно, использует разные алгоритмы поиска корней.

root(f(x),x);
root (f (x) , x, a, b);

f(x) — скалярная функция, определяющая уравнение f(x)=0;

х — имя скалярной переменной, относительно которой решается уравнение;

а, b — границы интервала, внутри которого происходит поиск корня.

Первый тип функции root, аналогично встроенной функции Find, требует дополнительного задания начального значения переменной х, для чего нужно просто перед применением функции root присвоить х некоторое число. Таким образом, присвоение начального значения требует априорной информации о примерной локализации корня, т. к. поиск корня будет производиться вблизи этого числа. Пример работы функции root объясняется листингом 5.13.

Листинг 5.13. Два варианта уравнения методом секущих

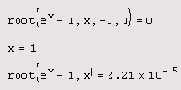
Как вы можете убедиться (первая строка листинга 5.13), для решения уравнения при помощи функции root (f (x) ,x,a,b) не требуется задавать начального приближения, а достаточно указать интервал [а,b]. Поиск корня будет осуществлен в промежутке между а и b альтернативным численным методом (Риддера или Брента). Когда root имеет четыре аргумента, следует помнить о двух ее особенностях. Во-первых, внутри интервала не должно находиться более одного корня, иначе будет найден один из них, заранее неизвестно, какой именно. Во-вторых, значения f (а) и f (b) должны иметь разный знак, иначе будет выдано сообщение об ошибке.

В чем же отличие встроенной функции Find от функции root? Оно состоит в том, что для решения одних и тех же задач используются различные численные алгоритмы (градиентные и метод секущих соответственно). В примерах уравнений с одним неизвестным, которые мы рассматривали до сего момента, выбор метода не влиял на окончательный результат, поскольку фигурировавшие в них функции были "хорошими", т. е. достаточно гладкими для поиска корня одним из градиентных методов, требующих, как известно, вычисления производных. Между тем бывают ситуации, когда применение того или иного метода имеет решающее значение.

Приведем пример простой функции f(x), корни которой удается отыскать только при помощи функции root (листинг 5.14). Она определена в первой строке этого листинга, а ее корень вычислен во второй строке. Из графика, представленного на рис. 5.5, видно, что f (х) имеет особенность в окрестности своего корня, являясь в ней разрывной. В завершающей части листинга 5.14 предпринимается попытка отыскать нулевое значение f (х) посредством вычислительного блока Given/Find, которая оказывается неудачной.

Листинг 5.14. Пример уравнения, которое удается решить только методом секущих

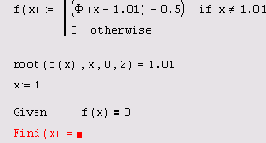
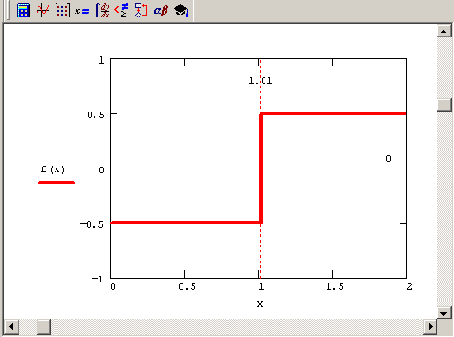
Рис. 5.5. Модельная функция f (х) (продолжение листинга 5.14)

Остается добавить, что f (х) может быть функцией не только х, а любого количества аргументов. Именно поэтому в самой функции root необходимо определить, относительно какого из аргументов следует решить уравнение. Эта возможность проиллюстрирована листингом 5.15 на примере функции двух переменных f (x,y)=x²-y²+1. В нем сначала решается уравнение f (х, 0) =0 относительно переменной х, а потом — другое уравнение f (0, у) =0 относительно переменной у, причем, благодаря удачному подбору начальных значений, вычисляются все корни данного квадратичного уравнения.

Таким образом, в обоих случаях один из аргументов функции f (х) воспринимается как неизвестное, а другой — как параметр. Не забывайте при численном решении уравнений относительно одной из переменных предварительно определить значения остальных переменных. Иначе попытка вычислить уравнения приведет к появлению ошибки "This variable or function is not defined above", в данном случае говорящей о том, что другая переменная ранее не определена.

ПРИМЕЧАНИЕ

Для того чтобы отыскать зависимость корней уравнения, вычисленных по одной переменной, от других переменных, разработаны специальные эффективные алгоритмы. Об одной из возможностей читайте в разд. 5.3.3.

Листинг 5.15. Поиск корней уравнения, зависящего от двух переменных

Содержание раздела