Глава 6.1.1. Локальный экстремум

Для поиска локальных экстремумов имеются две встроенные функции, которые могут применяться как в пределах вычислительного блока, так и автономно:

Minimize (f,x₁, ... ,х_M) — вектор значений аргументов, при которых функция f достигает минимума;
Maximize (f,x₁, ... ,х_M) — вектор значений аргументов, при которых функция f достигает максимума:

f (x1,..., х_M,...)—функция;

x₁,...,х_M — аргументы, по которым производится минимизация (максимизация).

ПРИМЕЧАНИЕ

Вычислительный блок (ключевое слово Given со следующими после него логическими выражениями) обычно используется в задачах на условный экстремум (см. следующий разд.).

В качестве примера рассмотрим задачу численного поиска экстремумов полинома четвертой степени f (х), график которого был приведен на рис. 6.1. Как известно, парабола четвертой степени имеет три точки экстремума, и все они видны на рис. 6.1.

Всем аргументам функции f предварительно следует присвоить некоторые значения, причем для тех переменных, по которым производится минимизация, они будут восприниматься как начальные приближения. Примеры вычисления локальных экстремумов функции одной переменной показаны в листингах 6.1—6.2. Поскольку никаких дополнительных условий в них не вводится, поиск экстремумов выполняется для любых значений х от -oo до oo.

Листинг 6.1. Поиск минимума функции одной переменной (для трех начальных значений x)

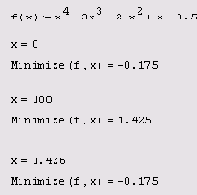
Листинг 6.2. Поиск максимума функции одной переменной

Как видно из листингов, существенное влияние на результат оказывает выбор начального приближения, в зависимости от чего в качестве ответа выдаются различные локальные экстремумы. Очень полезно сопоставить результаты минимизации (листинг 6.1) с графиком функции f(x) (см. рис. 6.1). Как видно, функция Minimize очень уверенно находит глубокий минимум х=-0.75. А вот на второй (плохо выраженный) минимум можно набрести лишь случайно, выбирая определенные начальные значения х. В последнем из трех примеров демонстрируется, что если взять начальное приближение х даже в непосредственной близости от этого локального минимума, численный метод все равно "сваливается" в первый, более глубокий минимум f(х). Попробуйте повторить расчеты, выбирая различные начальные значения, чтобы в этом убедиться.

В листинге 6.2 показаны аналогичные свойства функции Maximize. Если начальное приближение выбрать удачно, то итерационный процесс алгоритма сойдется к максимуму функции, а вот если выбрать его вдали от него, на участке f (х), где неограниченно возрастает (при х->±oo), численный метод вообще не справится с задачей, выдавая сообщение об ошибке. Это происходит, поскольку начальное приближение х=-10 выбрано далеко от области локального максимума, и поиск решения уходит в сторону увеличения f (х), т. е. расходится при х->oo.

ПРИМЕЧАНИЕ

Помните о возможности выбора численного алгоритма минимизации, который осуществляется при помощи контекстного меню (рис. 6.2). Не забывайте также, что, начиная с версии Mathcad 11, имеется возможность управлять параметром Multistart (Сканирование), при помощи которого можно попытаться организовать поиск глобального экстремума (см. разд. 5.3.2). Однако не слишком полагайтесь на эту опцию и, если перед вами стоит задача поиска глобального экстремума, постарайтесь организовать сканирование вручную.

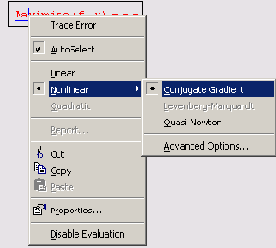
Рис. 6.2. Выбор численного метода минимизации

Содержание раздела