Математические задачи в пакете MathCAD 12
Глава 6.1.2. Условный экстремум
В задачах на условный экстремум встроенные функции минимизации и максимизации должны быть включены в вычислительный блок, т. е. им должно предшествовать ключевое слово
Given. В промежутке между Given и функцией поиска экстремума с помощью булевых операторов записываются логические выражения (неравенства, уравнения), задающие ограничения на значения аргументов минимизируемой функции. Листинги 6.3 и 6.4 содержат примеры поиска условного экстремума на различных интервалах, определенных неравенствами. У вас не должны возникнуть сложности с записью условий в Mathcad, а вот разобраться в скрытой от глаз вычислительной стороне будет полезно. С этой точки зрения поучительно сравнить результаты работы приведенных листингов с листингами 6.1 и 6.2 соответственно.
Листинг 6.3. Поиск условного минимума
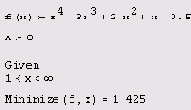
Листинг 6.4. Поиск условного максимума
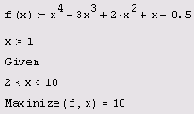
Как видно из листинга 6.3, если ограничить значения х интервалом, расположенным в окрестности правого локального максимума, с поиском которого мы встретили большие сложности при решении задачи на безусловный экстремум, то этот максимум будет без труда найден численным методом. Следует помнить также об одной особенности, иллюстрируемой листингом 6.4. А именно (в случае максимизации), если на границе интервала
f (x) достигает большего значения, нежели на локальном максимуме внутри интервала, то в качестве решения, скорее всего, будет выдано наибольшее значение (т. е. граница интервала).
Конечно, если на рассматриваемом интервале х расположено несколько локальных максимумов, ответ станет еще менее предсказуемым, поскольку будет напрямую зависеть от выбранного начального приближения. Не забывайте о важности его правильного выбора и в случае задач на условный экстремум. В частности, если вместо начального значения х=-1 задать
х=1, то в качестве максимума будет найдена правая граница интервала: Maximize (f,x) =2, что неверно, поскольку максимальное значение достигается функцией
f (х) на левой границе интервала при х=-3. Выбор начального приближения
х=-4 решает задачу правильно, выдавая в качестве результата Maximize(f,x)=-5.