Математические задачи в пакете MathCAD 12
Глава 6.1.5. Аналитическое решение задач на экстремум
Несмотря на то, что, как уже говорилось, разработчиками Mathcad символьное решение задач оптимизации не предусмотрено, пользователь все-таки имеет возможность аналитического исследования экстремумов функций, опираясь на базовые сведения математического анализа. Следует лишь вспомнить о том, что (при выполнении соответствующих условий на непрерывность и гладкость функции) точки экстремума
f(x) характеризуются тем, что в них производная этой функции проходит через нулевое значение. Тип экстремума (максимум или минимум) определяется знаком второй производной в этой точке.
Таким образом, имея в виду данные правила, не представляет особого труда организовать аналитическое решение задачи на экстремум, центральным моментом которого будет решение алгебраического уравнения
f (x)=0. Сразу стоит подчеркнуть, что можно использовать гибрид символьных и аналитических расчетов, когда, например, производная f (x) считается аналитически, а уравнение
f (x)=0 (если символьное решение получить не удается) — численно. В этом случае во всей красе может проявиться мощь
Mathcad, предоставляющего пользователю богатый арсенал как аналитических, так и численных методов.
Приведем несложный пример реализации аналитического поиска экстремумов той же функции (полинома 4-й степени), которая использовалась нами при демонстрации возможностей численных методов (см. разд. 6.1.1). В листинге 6.7, в первой строке, приводится определение
f(x), а затем при помощи символьного процессора осуществляется отыскание корней нелинейного уравнения
f (x)=0. Результатом решения являются все три точки экстремума (последняя строка листинга). На рис. 6.4 показан график функций
f (х) и f (x), и легко убедиться, что экстремумам исходной функции соответствуют нули ее производной.
Листинг 6.7. Аналитический поиск экстремумов функции
одной переменной
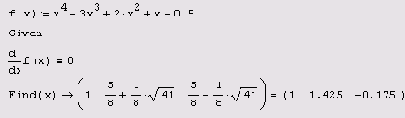
Чтобы завершить анализ f (х) на экстремумы, необходимо определить, какие из найденных точек являются точками минимума, а какие — максимума. Для этого (листинг 6.8) следует просто рассчитать значения второй производной в результатах решения уравнения и определить ее знак.
Листинг 6.8. Анализ типа точек экстремума (продолжение
листинга 6.7)
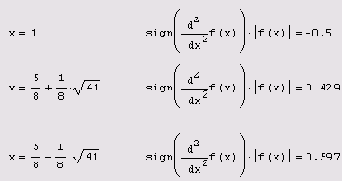
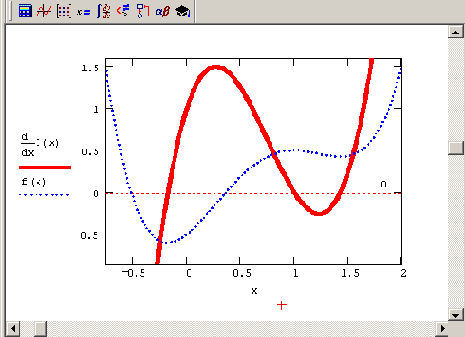
Рис. 6.4. Функция f (x) и ее производная (продолжение листинга 6.7)