Математические задачи в пакете MathCAD 12
Глава 6.3.1. О постановке некорректных задач
Рассмотрим сначала типичную постановку обратных задач, а затем обратимся к обсуждению корректности их постановки.
Обратные задачи
Строго говоря, обратные задачи связаны, как правило, не с отысканием значения корня уравнения (или системы) f (x)=o, а с вычислением неизвестной функции у (х), описываемой уравнением
S[y(x)]=b(x). (6.1)
Здесь A[у] — некоторый функционал (т. е. функция от функции), а
b(х) — известная функция (правая часть уравнения).
Рассмотрим типичную постановку обратных задач на примере так называемой инструментальной задачи. Пусть имеется некоторый сигнал у(х), который подвергается измерению на приборе, условно обозначаемом
S. Физику-исследователю доступно измерение данного сигнала, которое находится на
выходе прибора (дисплее, табло и т.п.). Обозначим это измерение
b(х). Поскольку прибор вносит в сигнал, во-первых, искажения (например, в устройствах типа спектрометров часто измеряются некоторые интегральные характеристики сигнала) и, во-вторых, шумовую компоненту. Формально данную физическую модель можно записать равенством (6.1), в котором оператором s обозначается аппаратная функция, т. е. действие прибора на сигнал
у (х).
Листинг 6.13. Пример моделирования прямой задачи, выражающей линейную
схему измерений
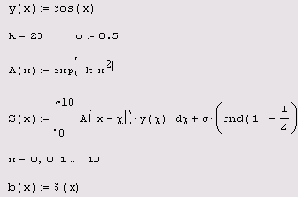
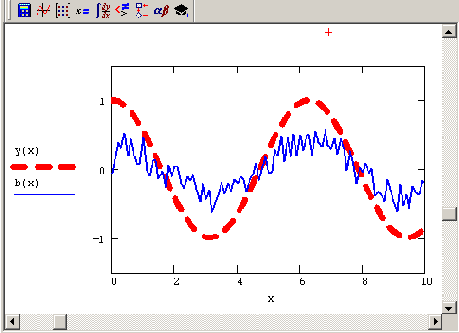
Рис. 6.6. Исходный сигнал и показания прибора (продолжение листинга 6.13)
Согласно изложенной модели, измерения b(х) могут довольно сильно отличаться от исходного сигнала у(х), что иллюстрируется простым примером
листинга 6.13 и рис. 6.6. В первой строке листинга выбирается модельный сигнал у(х), а во второй и третьей — определяется оператор
S[y(x)]. Важно отметить, что использованная структура оператора — интегральная зависимость от сигнала
у (х) в сумме с шумовой компонентой — наиболее типична для инструментальных обратных задач. Читателю будет очень полезно "поиграть" с параметрами задачи
k и сигма (эффективной шириной спектральной характеристики прибора и интенсивностью шума соответственно), чтобы "почувствовать" специфику модели измерений. Несколько примеров расчетов
b(х), согласно листингу 6.13, приведено на рис. 6.7 в виде коллажа нескольких графиков.
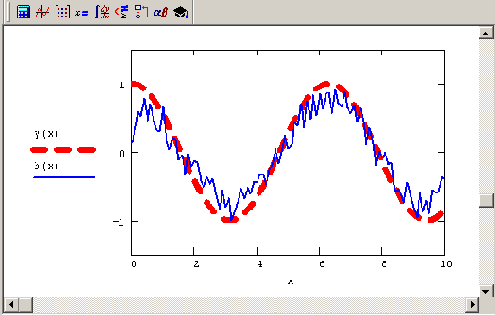
Рис. 6.7. Расчеты показаний прибора (коллаж результатов листинга 6.17 для различных сочетаний параметров k и 0)
ПРИМЕЧАНИЕ 1
Модель измерений, представленная в третьей строке листинга 6.13, описывает, с математической точки зрения, типичное интегральное уравнение, в которое неизвестная функция у(х) входит в виде части подынтегральной функции. Класс обратных задач чаще всего (но не всегда) соответствует как раз интегральным уравнениям.
ПРИМЕЧАНИЕ 2
Неизвестная функция у (х) входит в модель, приведенную в листинге 6.13, линейным
образом (в первой степени под знаком интеграла). В связи с этим рассматриваемая задача является линейной, а саму модель называют часто линейной схемой измерений. Линейность модели проявляется также в том, что ее дискретная форма записывается в виде матричного соотношения (см. листинг 6.14 ниже).
Из сказанного выше понятно, что в практических приложениях весьма актуальна задача восстановления сигнала у(х)
по показаниям прибора b(х) (при наличии определенной дополнительной информации о физике измерения, т. е. об операторе
S, выражающем действие прибора). Таким образом, в отличие от прямой задачи, выражающейся равенством (6.1), обратной задачей является восстановление функции
у (х) по известной b(х).
Обычно сигнал (и, соответственно, его измерение) может зависеть от времени и/или пространственных координат. Эту зависимость мы обозначили как зависимость от х. При использовании численных методов непрерывные зависимости от х дискретизируются, заменяясь соответствующими векторами. Таким образом, задача отыскания неизвестной функции
у(х) заменяется задачей поиска неизвестного вектора Y и может быть записана в матричном виде
S(Y)=B, (6.2)
где вектор у неизвестен, а оператор S (в линейном случае S(Y)=AY, где
А — матрица) и вектор правых частей уравнений в известны. Таким образом, в дискретном случае обратная задача для рассматриваемой математической модели состоит в решении системы (в общем случае, нелинейных) уравнений (6.2). Построенная описанным способом дискретная задача представлена в листинге 6.14. Важно отметить, что, поскольку исходная задача линейна, дискретный вариант ее оператора записывается в виде матрицы
А, а сама задача сводится к системе линейных алгебраических уравнений AY=B.
ПРИМЕЧАНИЕ
Рекомендуем читателю обратиться к соответствующему файлу Mathcad на прилагаемом к книге компакт-диске и сравнить графики сигнала и измерений, соответствующие непрерывной (интегральной) и дискретной (матричной) модели. Будет очень полезным осуществить расчеты для разных значений параметров, в том числе количества точек дискретизации м, а также разобраться, какова структура матрицы
А.
Листинг 6.14. Дискретная форма прямой задачи линейной
модели измерений (продолжение листинга 6.13)
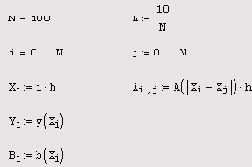
Некорректные задачи
При решении обратных задач важную роль играет их устойчивость. Задача устойчива, если малым флуктуациям правых частей, т. е. вектора в, соответствуют малые флуктуации решения Y. Иными словами, устойчивость по правой части состоит в требовании, чтобы решения близких задач
AY=B и AY=B+σB мало отличались друг от друга. Если задача изначально является неустойчивой, то решать ее нет смысла, поскольку погрешности алгоритмов, накапливающиеся в ходе решения численными методами, неизбежно приведут к тому, что будет найдено неверное решение.
Как правило (в том числе в нашем примере), обратные задачи характеризуются наличием шумов, что может быть символически отражено равенством (если опять-таки предположить, что шум ст входит в схему измерений линейно):
AY+σ=B. (6.3)
Наличие шума коренным образом меняет идеологию решения обратных задач. Если сама задача является устойчивой, то существование шума может эту устойчивость нарушать. Попросту говоря, различные (даже очень сильно отличающиеся) сигналы
Y1 и Y2 могут, будучи искажены шумом, приводить к очень похожим измерениям
В1~B2. Поэтому встает вопрос, можно ли извлечь из измерений полезную информацию о сигнале, если наличие шума делает задачу неустойчивой? Такие задачи называются задачами, поставленными некорректно, и для их решения развиты специальные методы, основанные на привлечении дополнительной априорной информации о решении Y, которые будут рассмотрены ниже. Следует также отметить, что класс некорректных задач шире класса обратных (один из примеров вы найдете в конце разд. 11.1.2).
Сказанное иллюстрирует рис. 6.8, на котором представлена попытка решения задачи листингов 6.13 и 6.14 "в лоб", прямым обращением матрицы А. Реконструкция сигнала путем простого обращения матрицы А оказывается возможной лишь для очень низких значений уровня шума а, а при увеличении шума решение
Y=A-1B оказывается совершенно нефизическим. Очевидно, что для получения осмысленного результата следует применять иные методы.
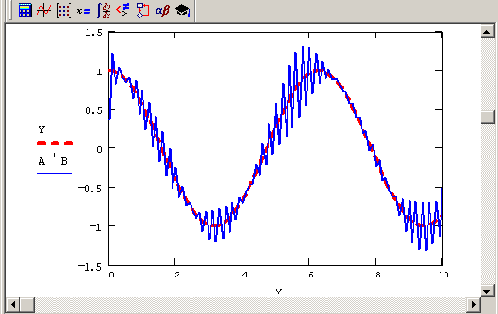
Рис. 6.8. Исходный сигнал и попытка его реконструкции А-1В (продолжение листингов 6.13 и 6.14) для
σ=10-5
ПРИМЕЧАНИЕ
Проблемы, возникающие при попытке обращения матрицы А, связаны с ее плохой обусловленностью. Подход к подобным задачам может быть не обязательно таким, как рассказывается в двух следующих разделах (см. главу 8).