Математические задачи в пакете MathCAD 12
Глава 6.3.3. Регуляризация Тихонова
Говоря о некорректных задачах, нельзя не отметить, что для их решения советским математиком Тихоновым был предложен чрезвычайно эффективный метод, называемый регуляризацией и основанный на привлечении дополнительной априорной информации о решении, которая может быть как качественной, так и количественной. Например, можно искать решение, максимально близкое к некоторому профилю, т. е. к некоторому вектору
Y0. Концепция регуляризации сводится к замене исходной некорректной задачи на задачу о минимизации следующей функции:
Ω(Y,λ) = |АY-B|+λ|Y-Y0|, (6.5)
где λ — малый положительный параметр регуляризации, который необходимо подобрать определенным способом. Отметим, что, если рассматривать не дискретную, а непрерывную задачу (т. е. профиль
у(х) вместо вектора Y), то Ω(у(х),λ) будет представлять собой не функцию, а функционал, исторически называемый функционалом Тихонова.
Минимизируя функцию Ω(Y,λ), можно получить регуляризованное решение
Y (А), зависящее от параметра λ. Из (6.5) хорошо ясен его смысл: при малых
λ ~ 0 проблема поиска функционала близка к (некорректной) исходной задаче, а при больших
А, задача поставлена корректно, но ее решение далеко от решения исходной обратной задачи. А именно, чем больше параметр регуляризации, тем ближе решение к априорной оценке
Y0. Очевидно, что на практике необходимо выбирать промежуточные
λ.. Можно показать, что в линейном случае задача о минимизации функционала
Ω(Y,λ) может быть сведена к следующей системе линейных алгебраических уравнений (решению линейных систем посвящена глава 8):
(ATA+λI)Y=ATB+λY0. (6.6)
ПРИМЕЧАНИЕ
В общем (нелинейном) случае минимизация Ω(Y,λ) должна производиться по всем компонентам вектора
Y, что представляет собой довольно громоздкую вычислительную задачу. Как уже отмечалось, поиск глобального экстремума
осложняется не только благодаря многомерности задачи, но и из-за возможности существования нескольких локальных минимумов.
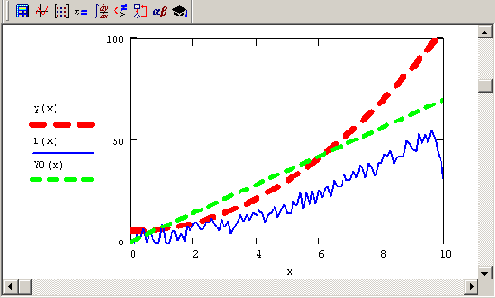
Рис. 6.10. Исходный сигнал Y, его априорная оценка 0 и измерения В (продолжение листинга 6.16)
Приведем в качестве примера применения регуляризации (листинг 6.16) решение некорректной линейной задачи интерпретации измерений, которая решалась нами ранее другими способами в листингах 6.13—6.15. В качестве модельного сигнала будем использовать квадратичную параболу, а в качестве априорной оценки — линейный профиль
Y0 (рис. 6.10). Сделаем мы это для того, чтобы соблюсти честность, пытаясь подогнать регуляризованное решение не к исходной (вообще говоря, неизвестной) модели, а к иной зависимости. В результате решения (в последней строке листинга) системы линейных уравнений (6.6), зависящей от А. как от параметра, получается зависимость регуляризованного решения (вектора
Y) от X. Соответствующая невязка системы уравнений
δ(λ) = |AY(λ)-B|, также являющаяся функцией
X, показана на рис. 6.11.
Листинг 6.16. Регуляризация некорректной линейной задачи
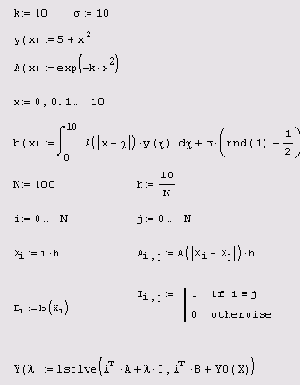
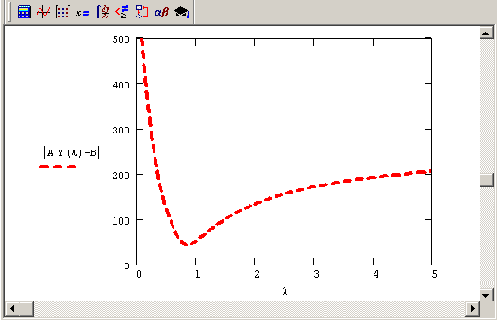
Рис. 6.11. Невязка δ(λ), даваемая регуляризованным решением Y(λ) задачи (6.6)
(продолжение листинга 6.16)
Для реконструкции можно использовать такое значение λ, которое соответствует глобальному минимуму зависимости
δ(λ). Иными словами, необходимо решить еще одну задачу на минимум, но уже другой функции
δ(λ) (листинг 6.17). Подчеркнем, что само определение этой функции подразумевает вложенную минимизацию функционала Тихонова (6.5), которую мы, правда, оформили посредством решения системы линейных уравнений (6.6). Таким образом, для построения реконструкции сигнала (она показана на рис. 6.12) нам пришлось решить две задачи минимизации.
ПРИМЕЧАНИЕ
Часто применяют и другой способ определения А, называемый принципом невязки. Он подразумевает выбор параметра регуляризации, с которым невязка приблизительно равна сумме погрешностей измерений (т. е. заданий правой части) и аппроксимации (погрешности, заложенной в матрице
А).
Листинг 6.17. Квазиоптимальный выбор параметра регуляризации
(продолжение листинга 6.16)
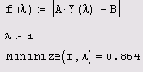
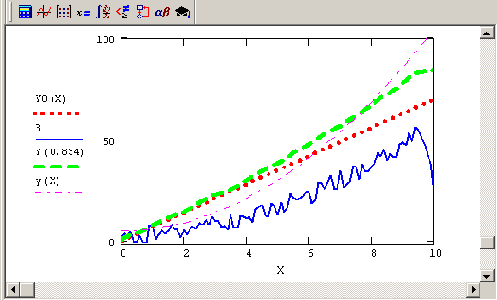
Рис. 6.12. Исходный сигнал Y и его регуляризованная реконструкция (продолжение листинга 6.17)