Математические задачи в пакете MathCAD 12
Глава 7.1.1. Транспонирование
Транспонированием называют операцию, переводящую матрицу размерности MxN в матрицу размерности
NxM, делая столбцы исходной матрицы строками, а строки — столбцами. Несколько примеров транспонирования приведены в листинге 7.1. Ввод символа транспонирования (transpose) осуществляется с помощью панели инструментов
Matrix (Матрица) или нажатием клавиш <Ctrl>+<!>. He забывайте, что для вставки символа транспонирования матрица должна находиться между линиями ввода.
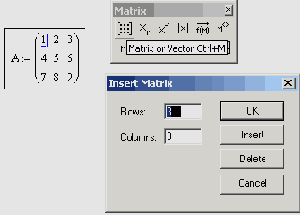
Рис. 7.1. Ввод матриц и основные операции над ними осуществляются при помощи панели Matrix
ПРИМЕЧАНИЕ
Все матричные и векторные операторы, о которых пойдет речь, допустимо использовать как в численных, так и в символьных расчетах. Мощь символьных операций заключается в возможности проводить их не только над конкретными числами, но и над переменными. Смело используйте символьный процессор в качестве мощного математического справочника, когда вы хотите вспомнить какое-либо определение из области линейной алгебры. Именно по этой причине мы прибегаем к примерам символьных расчетов в большинстве иллюстраций к данному разделу.
Листинг 7.1. Транспонирование векторов и матриц
