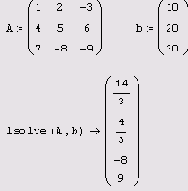Математические задачи в пакете MathCAD 12
Глава 8.1.2. Функция lsolve
Альтернативой способу решения СЛАУ, введенному в предыдущем разделе, является применение встроенной функции
isolve. Для этого система уравнений должна быть записана в матричной форме
Аx=b:
- isolve (А, b) — вектор решения системы линейных алгебраических уравнений:
- А — матрица коэффициентов системы;
- b — вектор правых частей.
ПРИМЕЧАНИЕ
В функции isolve запрограммирован численный метод LU-разложения (см. разд. 8.3.3), основанный на алгоритме последовательных исключений Гаусса. Он состоит в преобразовании матрицы А линейной системы к треугольному виду, т. е. к форме, когда все элементы ниже главной диагонали матрицы являются нулевыми (с/и. разд. 8.3.1). Точнее, исходная СЛАУ
Ах=b заменяется эквивалентной системой с другой матрицей А* и другим вектором правых частей
b*, но имеющей то же решение, что и исходная система. Очень важно заметить, что результат, выдаваемый методом Гаусса, является точным (конечно, с поправкой на неизбежно присутствующие ошибки численного округления, которые, в случае хорошо обусловленной матрицы А, являются ничтожными). Таким образом, в противоположность применению вычислительного блока
Given/Find (в основе которого лежит приближенный итерационный алгоритм), функция
isolve не нуждается в присвоении начальных значений вектору x.
Применение функции isolve показано в листинге 8.4. При этом матрица А может быть определена любым из способов, необязательно явно, как во всех примерах этого раздела. В последней строке листинга осуществляется вычисление нормы невязки, которая оказывается равной нулю. Заметим, что встроенную функцию
isolve допускается применять и при символьном решении СЛАУ (листинг 8.5). В последнем случае в уравнениях допускается использовать параметры (т. е. имена переменных, которым не присвоены никакие значения).
Листинг 8.4. Численное решение СЛАУ
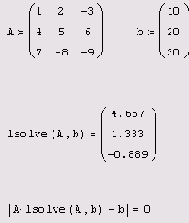
Листинг 8.5. Символьное решение СЛАУ (продолжение
листинга 8.4)