Математические задачи в пакете MathCAD 12
Глава 8.2.2. Недоопределенные системы
Альтернативным рассмотренному в предыдущем разделе классу СЛАУ с прямоугольной матрицей размера
MxN, (при M<N) является случай, когда количество уравнений меньше количества неизвестных. Как несложно сообразить, такие системы либо имеют бесконечное число решений, либо не имеют решения вовсе. Решение несовместной системы можно искать в смысле минимизации нормы невязки по методу наименьших квадратов (см. разд. 8.2.1 и 8.2.3). Ниже в этом разделе будут разобраны задачи, имеющие бесконечное множество решений.
О постановке задач
Пример аналитического решения системы двух уравнений с тремя неизвестными при помощи символьного процессора приведен в листинге 8.11.
Листинг 8.11. Аналитический поиск семейства решений
недоопределенной СЛАУ
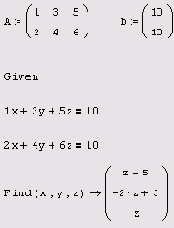
Приведенную простую систему двух уравнений нам удалось без труда решить аналитически, однако для решения недоопределенных систем, состоящих из большого числа уравнений, необходимо уметь использовать численные алгоритмы.
Рассмотрим в качестве еще одного модельного примера единственное уравнение с двумя неизвестными x0-2x1=l0. Хорошей визуализацией, подчеркивающей специфику данной задачи, будет график геометрического места его решений на плоскости (x0,xi) (рис. 8.4). Заметим, что на этом и на следующем рисунке мы использовали обозначение (для корректного построения графика) x0=z. Очевидно, что решений уравнения бесконечно много, и все они находятся на прямой линии
x1=(x0-10) /2.
Как и в предыдущем примере (листинг 8.11), нам удалось решить задачу аналитически, и опять-таки число решений получилось бесконечным. Для того чтобы получить возможность осмысленного численного решения подобных (уже не настолько тривиальных) задач, необходимо выделить из бесконечного множества решений одно, оправданное с математической точки зрения, и предложить алгоритм его поиска. Эта проблема решается посредством привлечения понятия нормального псевдорешения.
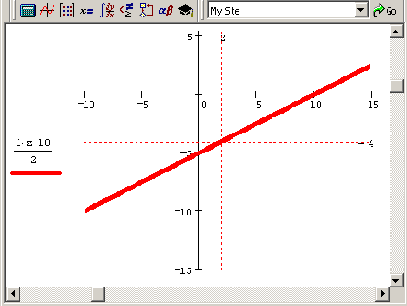
Рис. 8.4. График всех решений уравнения x0-2x1=10
Нормальное псевдорешение
Способ выбора одного решения из бесконечного множества, изображенного на рис. 8.4, подсказывает, по аналогии с переопределенными СЛАУ (см. разд. 8.2. Т), сам физический смысл задачи, которую можно интерпретировать как м измерений с
N неизвестными (M<N). Для того чтобы получить разумное единственное решение задачи, необходимо "доопределить" ее, добавив некоторые априорные соображения о значении неизвестного вектора х.
Если априорной информации о примерной величине вектора х нет, единственным образом решить СЛАУ невозможно. Однако если о неизвестном векторе хоть что-то можно сказать, данная информация позволит доопределить систему уравнений и получить решение, учитывающее как систему, так и априорную информацию. Иными словами, следует ввести в задачу определенные ожидания о величине вектора х. Математически, не теряя общности, можно полагать ожидаемое значение вектора
х нулевым, поскольку перейти от любого х к нуль-вектору можно простым линейным преобразованием переменных, которое изменит только вектор правой части
b.
Таким образом, вполне логично объявить решением недоопределенной СЛАУ такое из решений, которое ближе всего находится к нулевому вектору, т. е. обладает минимальной нормой
|х| -min. Это решение называют нормальным псевдорешением СЛАУ, и искать его следует, минимизируя норму
вектора х на предварительно полученном семействе решений СЛАУ. Иными словами, решение недоопределенной СЛАУ сводится к условной минимизации функции
|х| (рис. 8.5). Геометрический смысл нормального псевдорешения (в рассматриваемом случае одного уравнения с двумя неизвестными) очевиден: это точка, лежащая на пересечении прямой семейства всех решений и перпендикуляра к этой прямой, восстановленного из начала координат. На рис. 8.4 нормальное псевдорешение выделено пунктирными линиями.
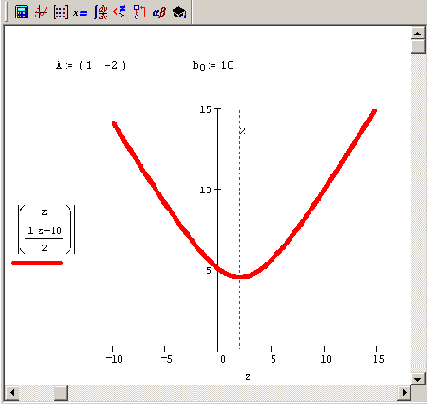
Рис. 8.5. График функции f (x0) = |х| при условии, что xc-2xi=10
Принимая во внимание введенную технику решения недоопределенных СЛАУ, можно предложить для этих задач простой и понятный алгоритм, опирающийся на встроенную функцию
Minimize. В листинге 8.12 решена задача численного отыскания псевдорешения рассматриваемого единственного уравнения (рис. 8.5), а в листинге 8.13 — решение недоопределенной системы двух уравнений с тремя неизвестными, которая исследовалась аналитически в листинге 8.11 (см. предыдущий разд.). Как уже отмечалось, смысл обоих листингов заключается в минимизации нормы искомого вектора при условии, что выполнена система равенств
Aх=b. Графики функции f (х) = |х|, при условии выполнения СЛАУ из листингов 8.12 и 8.13, изображены на рис. 8.5 и 8.6 соответственно.
Листинг 8.12. Поиск нормального псевдорешения уравнения
x0-2xi=10
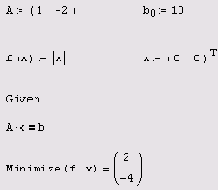
ПРИМЕЧАНИЕ
Возвращаясь к примеру с грушами и яблоками (см. разд. 8.2), можно интерпретировать недоопределенную СЛАУ из листинга 8.12 как единственное измерение, которого недостаточно для однозначного определения веса одной груши и одного яблока. Однако если учесть априорную оценку об этих весах (пусть даже весьма грубую), это позволит отыскать решение, которое будет осмысленным. Конечно, в этом случае следует выбрать соответствующий вектор априорной оценки (в третьей строке листинга 8.12) и, кроме того, добавить дополнительное условие на положительную определенность неизвестных, как в листинге 8.10 (см. раза. 8.2.2).
Листинг 8.13. Поиск нормального псевдорешения
недоопределенной СЛАУ
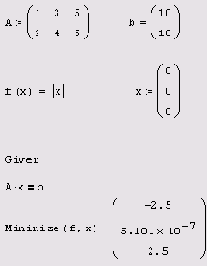
ПРИМЕЧАНИЕ
Если недоопределенная СЛАУ не имеет бесконечного множества решений, а является несовместной, то способ, предложенный в листинге 8.13, использовать нельзя, т. к. условие заведомо невыполнимо. Подход к решению таких задач заключается в поиске компромиссного решения, минимизирующего как норму невязки, так и норму решения (см. разд. 8.2.3).
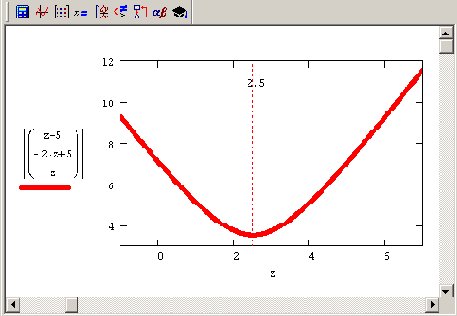
Рис. 8.6. График функции f (х2) = |х| при условии выполнения СЛАУ из листинга 8.13