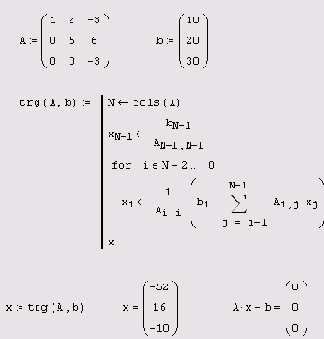Математические задачи в пакете MathCAD 12
Глава 8.3.1. СЛАУ с треугольной матрицей
Начнем разговор о решении СЛАУ посредством матричных разложений с простого, но исключительно важного частного случая, а именно, систем с треугольной матрицей, т. е. такой матрицей, по одну из сторон от диагонали которой находятся одни нули. В листинге 8.17 приведен пример верхнетреугольной
L матрицы (первая строка листинга), а также ряд формул, по которым за N операций рассчитывается решение соответствующей линейной системы. Из этого примера ясно, что сведение задачи общего вида к СЛАУ с треугольной матрицей практически решает эту задачу, поскольку гарантировано получение результата за минимальное число операций.
ПРИМЕЧАНИЕ 1
Подчеркнем, что мы нарочно оформили расчет решения треугольной СЛАУ в виде пользовательской функции trg (A,b), для чего нам пришлось применить элементы программирования. Мы так поступили, чтобы иметь впоследствии возможность применять ее в качестве подпрограммы решения СЛАУ посредством различных матричных разложений, включая листинг 8.17 в последующие листинги. Более того, несложно модифицировать листинг 8.17 для решения нижнетреугольных систем, определив, таким образом, еще одну функцию
itrg (А,
b) (вы найдете соответствующий листинг на компакт-диске).
ПРИМЕЧАНИЕ 2
Алгоритм решения СЛАУ с треугольной матрицей называют иногда прямым ходом решения СЛАУ (часто подразумевая, что до него выполнены определенные преобразования, именуемые обратным ходом) либо просто подстановкой. В частности, решение еще одного часто встречающегося типа систем с трехдиагональной матрицей сводится к прямому и обратному ходу алгоритма, называемого прогонкой (см. разд. 11.2.2).
Листинг 8.17. Решение СЛАУ с треугольной матрицей (прямой
ход)