Математические задачи в пакете MathCAD 12
Глава 8.3.4. QR-разложение
Среди матричных разложений особую роль играют ортогональные преобразования, обладающие свойством сохранения нормы вектора. Напомним из курса линейной алгебры, что матрица
Q называется ортогональной, если QTQ=I, где I — единичная матрица. Свойство сохранения нормы вектора при ортогональных преобразованиях, т. е.
|Qx|=|x|, дает рецепт поиска псевдорешения вырожденных СЛАУ, а именно, замену исходной задачи минимизации невязки с "плохой" матрицей
|Аx-b| задачей |QT(Ax-b)|, в которой матрица уже будет "хорошей" благодаря специальному построению матрицы
Q. Таким образом, ортогональные разложения используются при решении любых систем (в том числе с прямоугольной матрицей А, причем как переопределенных, так и недоопределенных).
Одним из важнейших вариантов ортогональных разложений некоторой матрицы А является QR-разложение вида
A=QR, где Q — ортогональная матрица, а R — верхняя треугольная матрица:
- qr (A) — QR-разложение:
- А — вектор или матрица любого размера.
Результатом действия функции qr (А) является матрица, составленная из матриц Q и R соответственно (подобно рассмотренному в предыдущем разделе LU-разложению). Выделить матрицы QR-разложения несложно при помощи встроенной функции выделения подматрицы submatrix (листинг 8.22).
Листинг 8.22. QR-разложение сингулярной матрицы
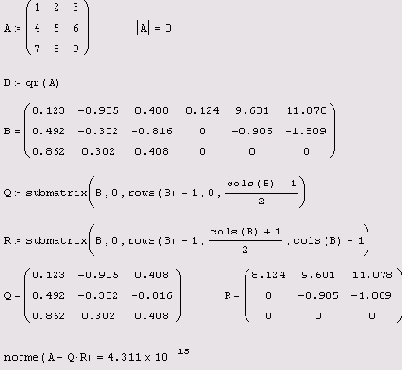
Если бы исходная СЛАУ Aх=b не была вырожденной, то можно было сразу записать:
QTQ-Rx=QTb, откуда следует (благодаря ортогональности матрицы
Q): Rx=QTb. Так как матрица к — треугольная, решение данной системы получается по формулам прямого хода. Если использовать нашу пользовательскую функцию решения треугольной системы (см. разд. 8.3. Т), то результат исходной СЛАУ запишется в виде одной строки кода: trg(R,QTb) (соответствующий пример решения невырожденной СЛАУ вы найдете на компакт-диске).
Обратимся теперь к проблеме решения СЛАУ с сингулярной квадратной NxN или прямоугольной
NxM матрицей А. Если ее ранг равен k (он может быть меньше N и м, как в листинге 8.22, где
N=M=S, a k=2), то получающаяся треугольная матрица R имеет следующую структуру:
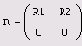
где R1 — верхняя треугольная матрица, a R2 — просто некоторая матрица, а нули обозначают, в общем случае, нулевые матрицы соответствующих размеров.
Если система вырожденная, то она имеет бесконечное множество псевдорешений (векторов, минимизирующих норму невязки). При помощи QR-разложения можно сразу выписать одно из них (правда, не обладающее минимальной нормой). В нашем примере последняя строка матрицы
R содержит одни нули, поэтому последняя компонента вектора псевдорешения х может быть абсолютно любой. Если положить
х2=0, то остальные компоненты х определятся из треугольной СЛАУ R1x=QTb, как это проиллюстрировано листингом 8.23.
Листинг 8.23. Поиск одного из псевдорешений вырожденной
СЛАУ посредством QR-разложения (продолжение
листинга 8.22 )
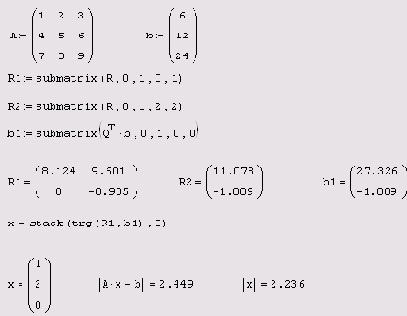
Для того чтобы выбрать из всего множества псевдорешений (минимизирующих невязку исходной СЛАУ) нормальное псевдорешение (т. е. обладающее минимальной нормой), необходимо решить соответствующую задачу минимизации (см. разд. 8.2.3). Если построено QR-разложение, сделать это намного легче. Если произвольную компоненту решения обозначить переменной
у: х2=у, то она определится из соответствующей задачи оптимизации (листинг 8.24, 1—3 строки), а остальные составляющие самого решения
х — из треугольной СЛАУ R1x=QTb-R2y. В последней строке листинга выводится полученное нормальное псевдорешение, а также его норма и соответствующая норма невязки (которые полезно сравнить с результатом прошлого листинга). Вспомогательный рис. 8.13 помогает понять структуру минимизируемой функции из листинга 8.24.
Листинг 8.24. Нормальное псевдорешение вырожденной СЛАУ
(продолжение листингов 8.22 и 8.23)

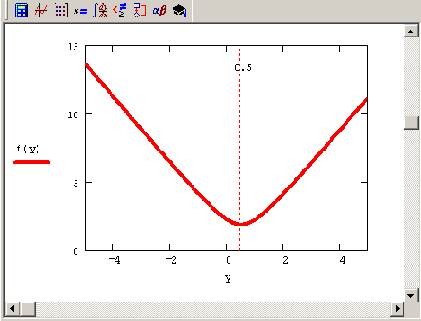
Рис. 8.13. Норма псевдорешения в зависимости от у (продолжение листинга 8.24)
Резюмируя практические аспекты применения QR-разложения, надо отметить, что алгоритмы решения СЛАУ на его основе практически одинаковы как для хорошо обусловленных, так и для сингулярных систем.
ПРИМЕЧАНИЕ
На прилагаемом к книге компакт-диске вы найдете дополнительные примеры построения QR-разложения как для квадратной, так и прямоугольной матрицы А.