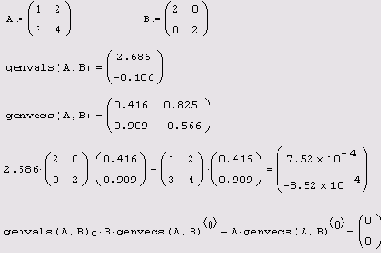Математические задачи в пакете MathCAD 12
Глава 8.4. Собственные векторы и собственные значения матриц
Завершим главу, посвященную решению СЛАУ, еще одной задачей вычислительной линейной алгебры — задачей отыскания собственных векторов х и собственных значений А, матрицы А, т. е. решения матричного уравнения
Ах=λх. Такое уравнение имеет решения в виде собственных значений
λ1,λ2, ... и соответствующих им собственных векторов
x1,x2,... Для решения таких задач на собственные векторы и собственные значения в Mathcad встроено несколько функций, реализующих довольно сложные вычислительные алгоритмы:
- eigenvais (A) — вычисляет вектор, элементами которого являются собственные значения матрицы А;
- eigenvecs (A) — вычисляет матрицу, содержащую нормированные собственные векторы, соответствующие собственным значениям матрицы А. n-й столбец вычисляемой матрицы соответствует собственному вектору n-го собственного Значения, вычисляемого eigenvais;
- eigenvec(A,λ) — вычисляет собственный вектор для матрицы А и заданного собственного значения А.:
- А — квадратная матрица.
Применение этих функций иллюстрирует листинг 8.27. В его конце приведена проверка правильности нахождения первого из собственных векторов и собственных значений, причем подстановка результата в выражение Аx=λx проведена дважды — сначала на числовых значениях х и λ, а потом путем перемножения соответствующих матричных компонентов.
Листинг 8.27. Собственные векторы и собственные значения матрицы
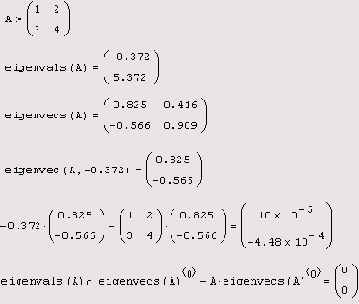
Помимо рассмотренной проблемы поиска собственных векторов и значений иногда рассматривают более общую задачу, называемую задачей на обобщенные собственные значения:
Ах=λBх. В ее формулировке помимо матрицы А присутствует еще одна квадратная матрица в. Для задачи на обобщенные собственные значения имеются еще две встроенные функции, действие которых аналогично рассмотренным (листинг 8.28):
- genvais (А,В) — вычисляет вектор v собственных значений, каждый из которых удовлетворяет задаче на обобщенные собственные значения;
- genvecs (А, B) — вычисляет матрицу, содержащую нормированные собственные векторы, соответствующие собственным значениям в векторе v, который вычисляется с помощью genvals. В этой матрице i-й столбец является собственным вектором х, удовлетворяющим задаче на обобщенные собственные значения:
Листинг 8.28. Поиск обобщенных собственных векторов и собственных значений
- А, B — квадратные матрицы.