Глава 9.1.2. Фазовый портрет динамической системы

Модели, основанные на задачах Коши для ОДУ, часто называют динамическими системами, подчеркивая, что, как правило, они содержат производные по времени t и описывают динамику некоторых параметров. Проблемы, связанные с динамическими системами, на самом деле весьма разнообразны и зачастую не сводятся к простому интегрированию ОДУ. Некоторые из них мы обозначим в данном разделе, отметив, что для изучения динамических систем центральным моментом является анализ фазовых портретов, т. е. решений, получающихся при выборе всевозможных начальных условий.

Решение ОДУ часто удобнее изображать не в виде графика у₀ (t), y₁(t), ..., как на рис. 9.1, а в фазовом пространстве, по каждой из осей которого откладываются значения каждой из найденных функций. При таком построении графика аргумент t будет присутствовать на нем лишь параметрически. В рассматриваемом случае двух ОДУ (мы свели к ним в предыдущем разделе дифференциальное уравнение осциллятора второго порядка) фазовое пространство является координатной плоскостью, а решение представляет собой кривую, или, по-другому, траекторию, выходящую из точки, координаты которой равны начальным условиям (рис. 9.2). В общем случае, если система состоит из N ОДУ, то фазовое пространство является N-мерным. При N>3 наглядность теряется, и для визуализации фазового пространства приходится строить его различные проекции или прибегать к другим специальным приемам (например, отображению Пуанкаре).

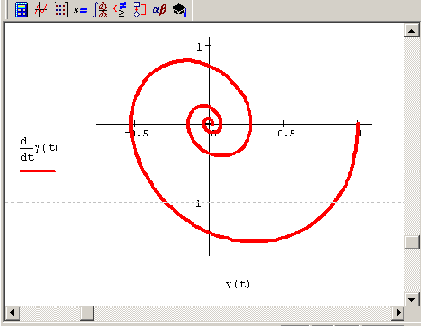
Рис. 9.2. Решение уравнения w²у' '+βу'+у=0 на фазовой плоскости (продолжение листинга 9.1)

Как правило, решение задач Коши для ОДУ и их систем — задача хорошо разработанная и с вычислительной точки зрения довольно простая. На практике чаще встречаются другие, более сложные задачи, в частности, исследование поведения динамической системы в зависимости от начальных условий. При этом в большинстве случаев бывает необходимым изучить только асимптотическое решение ОДУ, т.е. y(t->∞), называемое аттрактором. Очень наглядным образом можно визуализировать такую информацию на фазовой плоскости, во многом благодаря тому, что существует всего несколько типов аттракторов, и для них можно построить четкую классификацию.

С одной стороны, каждое решение будет выходить из точки, координаты которой являются начальными условиями, но, оказывается, для большинства ОДУ целые семейства траекторий будут заканчиваться в одних и тех же аттракторах (стационарных точках или предельных циклах). Множество решений, вычисленное для всевозможных начальных условий, образует фазовый портрет динамической системы. С вычислительной точки зрения задача исследования фазового портрета часто сводится к обычному сканированию семейств решений ОДУ при разных начальных условиях.

ПРИМЕЧАНИЕ

Для рассматриваемого примера модели гармонического осциллятора имеется единственная стационарная точка (аттрактор), на которую "накручивается" решение, из каких бы начальных условий оно ни выходило. В теории динамических систем аттрактор такого типа называется фокусом.

Дальнейшее усложнение задач анализа фазовых портретов связано с их зависимостью от параметров, входящих в систему ОДУ. В частности, при плавном изменении параметра модели может меняться расположение аттракторов на фазовой плоскости, а также могут возникать новые аттракторы и прекращать свое существование старые. В первом случае, при отсутствии особенностей, будет происходить простое перемещение аттракторов по фазовой плоскости (без изменения их типов и количества), а во втором — фазовый портрет динамической системы будет коренным образом перестраиваться. Критическое сочетание параметров, при которых фазовый портрет системы качественно меняется, называется в теории динамических систем точкой бифуркации.

Поясним понятие бифуркации на примере той же модели осциллятора, которая зависит от двух параметров (ш и р). При р>о существует единственная стационарная точка типа фокуса (см. рис. 9.2), которая в точке бифуркации Р=о вырождается в аттрактор типа центр, характеризующийся тем, что решения ОДУ представляют собой циклы, совершаемые вокруг этой точки с амплитудой, которая существенно зависит от начальных условий (рис. 9.3). Для надежного исследования фазового портрета практически всегда необходимо решить систему ОДУ большое количество раз с самыми разными начальными условиями (и, возможно, с разным набором параметров модели), чтобы посмотреть, к каким аттракторам сходятся различные траектории.

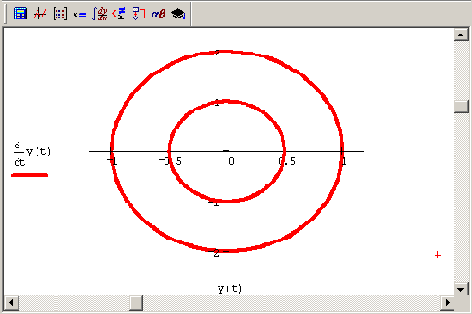
Рис. 9.3. Решение уравнения со2-у' '+у=0 для различных начальных условий (коллаж графиков)

Резюмируя содержание вводного раздела главы, перечислим еще раз типичные постановки задач, характерные для динамических систем:

решение одной задачи Коши для ОДУ;
исследование фазового портрета (поиск аттракторов);
отыскание зависимости положения аттракторов в фазовом пространстве от параметров модели и фиксация бифуркационных значений параметров.

В дальнейших разделах этой главы при рассказе о возможностях Mathcad мы будем в первую очередь описывать решение первой (базовой) задачи, для которой предусмотрен целый арсенал средств. А именно: вычислительный блок для решения ОДУ (см. разд. 9.2), несколько встроенных функций для решения систем ОДУ (см. разд. 9.3), в том числе жестких, которые не поддаются решению стандартными методами (см. разд. 9.4). Приемы, которые автор рекомендует в качестве идиом решения остальных задач, будут рассмотрены эпизодически, на конкретных примерах классических динамических систем вычислительной физики, химии и биологии (см. разд. 9.5 и 9.4.3), связанных с динамическими системами. В частности, программа для визуализации фазового портрета рассмотрена в конце главы, на примере модели брюсселятора (см. разд. 9.5.4). Сводка алгоритмов с рекомендациями по их применению в зависимости от типа задачи приведена конспективно, без детального разбора (см. разд. 9.3.4).

Содержание раздела