Глава 9.4.2. Функции для решения жестких ОДУ

Решение жестких систем дифференциальных уравнений можно осуществить только с помощью встроенных функций, аналогичных по действию семейству рассмотренных выше функций для обычных ОДУ:

Radau(y0,t0,t1,M,F) — алгоритм RADAUS для жестких систем ОДУ;
stiffb(y0,t0,1,M,F, J) — алгоритм Булирша—Штера для жестких систем ОДУ;
stiffr (y0, t0, t1,M, F, J) — алгоритм Розенброка для жестких систем ОДУ:

у0 — вектор начальных значений в точке to;

t0,t1 — начальная и конечная точки расчета;

M — число шагов численного метода;

F — векторная функция F(t, у) размера 1xN, задающая систему ОДУ;

J — матричная функция j(t,y) размера (N+1)xN, составленная из вектора производных функции F(t,y) no t (правый столбец) и ее якобиана (N левых столбцов).

Как вы можете заметить, для двух последних функций серьезным отличием от функций, решающих нежесткие системы, является добавление к стандартному набору параметров дополнительной матричной функции, задающей якобиан системы ОДУ. Решение выдается в виде матрицы, по форме идентичной аналогичным функциям решения нежестких задач Коши.

ПРИМЕЧАНИЕ

Встроенная функция Radau, которая не требует явного задания якобиана системы уравнений, появилась в версии Mathcad 2001I, а остальные две — в Mathcad 2001.

Решение жесткой задачи из предыдущего раздела при помощи функции Radau приведено в листинге 9.9. Результат показан в виде графика на рис. 9.14 вместе с графиком решения менее жесткой задачи (для которого применялся листинг 9.8). Как вы видите, хватило всего пяти точек разбиения интервала интегрирования жесткого ОДУ, чтобы метод с ним справился. Специфика применения других встроенных функций, требующих дополнительного задания якобиана, будет рассмотрена в следующем разделе на примере уравнения химической кинетики.

Листинг 9.9. Решение жесткого ОДУ алгоритмом RADAUS

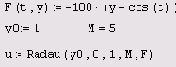
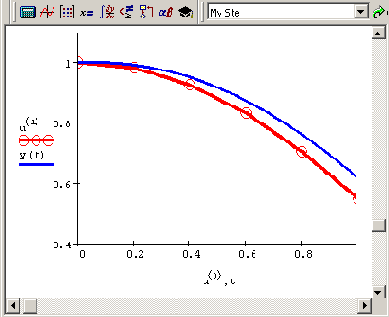
Рис. 9.14. Решение жесткого ОДУ методом RADAUS (продолжение листингов 9.8 и 9.9)

В заключение приведем соответствующие встроенные функции, которые применяются для решения жестких систем ОДУ не на всем интервале, а только в одной заданной точке t1.

radau(y0, t0, t1, асc, F, k, s) — метод RADAUS.
stiffb(y0,t0,t1,acc,F, J, k, s) — метод Булирша—Штера.
stiffr (y0,t0, t1, acc, F, J, k, s) — метод Розенброка.

Имена этих функций пишутся со строчной буквы, а их действие и набор параметров полностью аналогичны рассмотренным нами ранее для функций, относящихся к решению в заданной точке нежестких систем (см. разд. 9.3.2). Отличие заключается в специфике применяемого алгоритма и необходимости задания матричной функции якобиана J(t,y) (для двух последних функций).

Содержание раздела