Математические задачи в пакете MathCAD 12
Глава 10.5.3. Разностные схемы
Решение краевых задач при помощи разностных схем связано с необходимостью разработки собственного алгоритма для каждой конкретной задачи. Как вы помните (см. разд. 10.4), в случае линейных уравнений в результате построения разностной схемы система алгебраических сеточных уравнений также получалась линейной. Это автоматически означало, что она имеет единственное решение, которое в большинстве случаев могло быть найдено стандартными численными методами. В ситуации, когда исходные дифференциальные уравнения нелинейны, система разностных уравнений тоже является нелинейной, и их решение существенно усложняется, хотя бы потому, что оно не является единственным. Поэтому подход к построению разностных схем нелинейных уравнений должен быть специфическим, но наградой за него станет решение задач, с которыми не справляется алгоритм стрельбы (например, жестких).
Подробная разработка алгоритмов и соответствующих программ Mathcad выходит далеко за пределы данной книги, поэтому мы конспективно представим один из приемов решения нелинейных краевых задач, сводящийся к их линеаризации. В общих чертах подход заключается в следующем. Предположим, что некоторое приближение (обозначим его
Y(х) и у(х)) к решению нелинейной задачи (10.9) нам известно, и можно считать, что
Y->Y+Z и
y->y+z, где z и z — близкие к нулю функции х. Тогда, пользуясь их малостью (по сравнению с
Y0 и у0), можно разложить нелинейные слагаемые в уравнениях (10.9) в ряд Тейлора по
z и z. Получим:
Y'+Z' = -aY + ry + ε(Y2 + Yy) - aZ + rz + 2εY(Z + z);
(10.10)
y'+z' = ay - rY - ε(y2 + Yy) + az - rz - 2εy(Z + z)
.
Теперь, поскольку Y(x) и у(х) являются приближением к решению исходной задачи, то можно считать, что они (приблизительно) удовлетворяют и уравнению, и граничным условиям. Тогда, вычитая (10.9) из (10.10), получим краевую задачу для
z (х) и z (х):
Z' = -aZ + rz + 2εY(Z + z);
z' = az - rZ - 2εy(Z + z) ; (10.11)
Z(0) = z(0) = Z(l) = z(l) = 0.
Это и есть та самая новая задача для "маленьких" функций z (х) и
z (х), которую надо решить, и которая, благодаря малости z и z, является линейной. Вся беда в том, что мы не знаем "больших" функций
Y(x) и у(х), а они, увы, входят в задачу (10.11). Тем не менее рецепт получения этих функций напрашивается сам собой: если нелинейность исходных ОДУ не слишком сильная, то в качестве
Y и у можно взять решение линейной краевой задачи, т. е. задачи (10.9) с
ε(х)=0 (см. разд. 10.4.1).
Сказанное иллюстрируют листинги 10.9 и 10.10, первый из которых решает линейную краевую задачу (являясь, фактически, небольшой модификацией листинга 10.7 из разд. 10.4.2), а второй решает линеаризованную задачу (10.11), учитывая результат листинга 10.9. В листинге 10.9 матрица о и вектор правых частей в являются разностной аппроксимацией ОДУ (ее первые N строк аппроксимируют первое уравнение, а оставшиеся
N строк — второе). Такой же смысл и точно такую же структуру имеют матрица с и вектор правых частей с для второй (линеаризованной) задачи (10.11). Для решения сеточных уравнений
Dу=B и Cz=G используется (конечно, весьма неэкономично) встроенная функция
isolve, реализующая алгоритм Гаусса.
Важно привлечь внимание читателя к последним строкам листинга 10.9. В них осуществляется интерполяция полученного решения системы сеточных уравнений для того, чтобы в нелинейной задаче (в листинге 10.10) можно было использовать непрерывные "большие" функции из линейной задачи. В последней строке листинга 10.10 осуществляется сложение "больших" и "маленьких" функций (результатов листингов 10.9 и 10.10) для получения полного решения нелинейной задачи (10.9), которое изображено на рис. 10.12.
Не будем давать дополнительных комментариев к Mathcad-программам, надеясь, что
читатель, заинтересовавшийся нелинейным примером со световыми пучками и эффектом
разогрева светом среды, сам разберется в листингах, тем более что техника разработки разностных схем была нами детально разобрана раньше (см. разд. 10.4).
Листинг 10.9.Решение линейной (приближенной)
краевой задачи

Листинг 10.10. Решение линеаризованной задачи (продолжение
листинга 10.9)

Последний важный момент, который следует обозначить, связан с решением задач, обладающих значительной нелинейностью. Решение, приведенное в листингах 10.9, 10.10 и на рис. 10.12, согласно самой постановке, должно не сильно отличаться от решения линейной краевой задачи, поскольку функции
z(x) и z(x) малы по сравнению с Y(x) и у(х). Если же нелинейность сильная, то решение может сильно отличаться от
Y и у, и линеаризация (10.11) будет просто неправильной. В этом случае следует слегка усложнить алгоритм решения нелинейной краевой задачи.
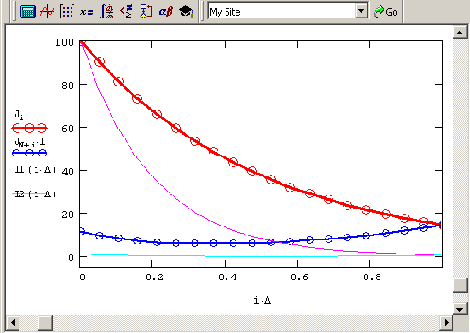
Рис. 10.12. Решение нелинейной краевой задачи разностным методом (продолжение листингов 10.9 и 10.10)
Обозначим полученное в результате решение, как и в листинге 10.10, вектором J(ε), подчеркивая тем самым его зависимость от параметра нелинейности. Очевидно, что
J(0) есть решение линейной задачи. Для того чтобы решить задачу с сильной нелинейностью, т. е. довольно большим
ε=ε1, можно организовать продолжение по
ε как по параметру. Иными словами, используя в качестве начального приближения
J (0), можно решить задачу для другого, малого
ε=Дε, получив
J(Aε), затем, взяв это J(ε)
в качестве приближенного решения, получить J(2Aε) и т. д. малыми шагами добраться до желаемого
ε1.
ПРИМЕЧАНИЕ
Упрощенную реализацию этого алгоритма вы найдете на компакт-диске, прилагаемом к книге. Она связана с выводом во внешний файл данных результата задачи из листинга 10.10 и считыванием из него же этих данных в качестве входной информации для следующей итерации. В качестве нулевой итерации используется решение линейной задачи, выводимое предварительно в файл из усовершенствованного листинга 10.9.