Глава 13.1.2. Кубическая сплайн-интерполяция

В большинстве практических приложений желательно соединить экспериментальные точки не ломаной линией, а гладкой кривой. Лучше всего для этих целей подходит интерполяция кубическими сплайнами, т. е. отрезками кубических парабол (рис. 13.4):

interp(s,x,y,t) — функция, аппроксимирующая данные векторов х и у кубическими сплайнами:

s — вектор вторых производных, созданный одной из сопутствующих функций cspline, pspline или lspline;

х — вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;

у — вектор действительных данных значений того же размера;

t — значение аргумента, при котором вычисляется интерполирующая функция.

Сплайн-интерполяция в Mathcad реализована чуть сложнее линейной. Перед применением функции interp необходимо предварительно определить первый из ее аргументов — векторную переменную s. Делается это при помощи одной из трех встроенных функций тех же аргументов (х, у):

ispline (х, у) — вектор значений коэффициентов линейного сплайна;
pspiine(x,y) — вектор значений коэффициентов квадратичного сплайна;
cspline (х, у) — вектор значений коэффициентов кубического сплайна:

х, у — векторы данных.

Выбор конкретной функции сплайновых коэффициентов влияет на интерполяцию вблизи конечных точек интервала. Пример сплайн-интерполяции приведен в листинге 13.2.

Листинг 13.2. Кубическая сплайн-интерполяция

Смысл сплайн-интерполяции заключается в том, что в промежутках между точками осуществляется аппроксимация в виде зависимости A(t)=at³+bt²+ ct+d. Коэффициенты а, b, с, d рассчитываются независимо для каждого промежутка, исходя из значений у* в соседних точках. Этот процесс скрыт от пользователя, поскольку смысл задачи интерполяции состоит в выдаче значения A(t) в любой точке t (рис. 13.4).

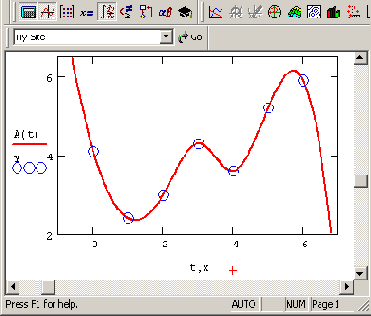
Рис. 13.4. Сплайн-интерполяция (продолжение листинга 13.2)

Чтобы подчеркнуть различия, соответствующие разным вспомогательным функциям cspline, pspline, ispline, покажем результат действия листинга 13.2 при замене функции cspline в предпоследней строке на линейную ispline (рис. 13.5). Как видно, выбор вспомогательных функций существенно влияет на поведение A(t) вблизи граничных точек рассматриваемого интервала (0,6) и особенно разительно меняет результат экстраполяции данных за его пределами.

В заключение остановимся на уже упоминавшейся в предыдущем разделе распространенной ошибке при построении графиков интерполирующей функции (см. рис. 13.3). Если на графике, например, являющемся продолжением листинга 13.2, задать построение функции А<Х) вместо A(t), то будет получено просто соединение исходных точек ломаной (рис. 13.6). Так происходит потому, что в промежутках между точками вычисления интерполирующей функции не производятся.

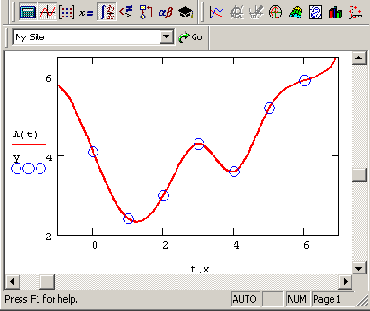
Рис. 13.5. Сплайн-интерполяция с выбором коэффициентов линейного сплайна lspline

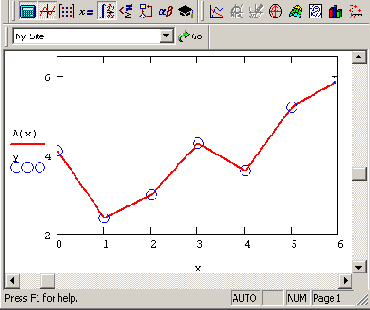
Рис. 13.6. Ошибочное построение графика сплайн-интерполяции (продолжение листинга 13.2)

Содержание раздела