Математические задачи в пакете MathCAD 12
Глава 13.1.3. Полиномиальная сплайн-интерполяция
Более сложный тип интерполяции — так называемая интерполяция В-сплайнами. В отличие от обычной сплайн-интерполяции (см. разд. 13.1.2), сшивка элементарных В-сплайнов производится не в точках
хi а в других точках
ui, координаты которых предлагается ввести пользователю. Сплайны могут быть полиномами 1, 2 или
3 степени (линейные, квадратичные или кубические). Применяется интерполяция В-сплайнами точно так же, как и обычная сплайн-интерполяция, различие состоит только в определении вспомогательной функции коэффициентов сплайна.
- interp(s,x,y,t) — функция, аппроксимирующая данные векторов х и у с помощью В-сплайнов.
- bspiine (x,y,u,n) — вектор значений коэффициентов В-сплайна:
- s — вектор вторых производных, созданный функцией bspline;
- х — вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;
- у — вектор действительных данных значений того же размера;
- t — значение аргумента, при котором вычисляется интерполирующая функция;
- u — вектор значений аргумента, в которых производится сшивка В-сплайнов;
- n — порядок полиномов онлайновой интерполяции (1, 2 или з).
ПРИМЕЧАНИЕ
Размерность вектора и должна быть на 1, 2 или 3 меньше размерности векторов
х и у. Первый элемент вектора и должен быть меньше или равен первому элементу вектора
х, а последний элемент и — больше или равен последнему элементу х.
Интерполяция В-сплайнами иллюстрируется листингом 13.3 и рис. 13.7.
Листинг 13.3. Интерполяция В-сплайнами

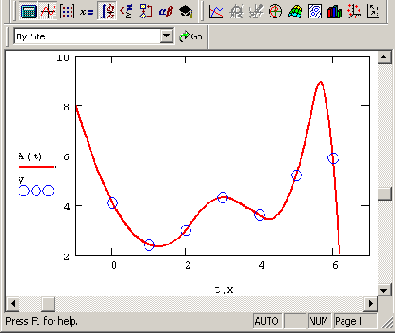
Рис. 13.7. В-сплайн-интерполяция (продолжение листинга 13.3)