Глава 13.2.2. Полиномиальная регрессия

В Mathcad реализована регрессия одним полиномом, отрезками нескольких полиномов, а также двумерная регрессия массива данных.

Полиномиальная регрессия

Полиномиальная регрессия означает приближение данных (x_i,y_i) полиномом k-й степени A(x)=a+bx+cx²+dx³+.. .+hx^k (рис. 13.16). При k=i полином является прямой линией, при k=2 — параболой, при k=3 — кубической параболой и т. д. Как правило, на практике применяются k<5.

ПРИМЕЧАНИЕ

Для построения регрессии полиномом k-й степени необходимо наличие, по крайней мере, (k+1) точек данных.

В Mathcad полиномиальная регрессия осуществляется комбинацией встроенной функции regress и полиномиальной интерполяции (см. разд. 13.1.2):

regress (х, у, k) — вектор коэффициентов для построения полиномиальной регрессии данных;
interp(s,x,y, t) — результат полиномиальной регрессии:

s=regress(х,у,k);

x — вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;

у — вектор действительных данных значений того же размера;

k — степень полинома регрессии (целое положительное число);

t — значение аргумента полинома регрессии;

ВНИМАНИЕ!

Для построения полиномиальной регрессии после функции regress вы обязаны использовать функцию interp

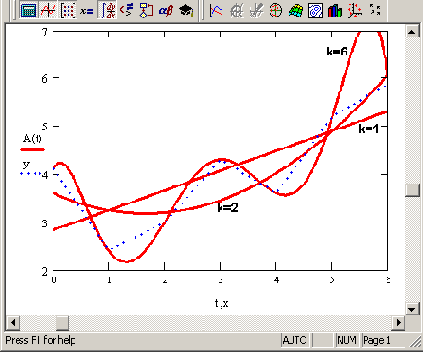
Рис. 13.16. Регрессия полиномами разной степени (коллаж результатов листинга 13.10 для разных k)

Пример полиномиальной регрессии квадратичной параболой приведен в листинге 13.10.

Листинг 13.10. Полиномиальная регрессия

Регрессия отрезками полиномов

Помимо приближения массива данных одним полиномом имеется возможность осуществить регрессию сшивкой отрезков (точнее говоря, участков, т. к. они имеют криволинейную форму) нескольких полиномов. Для этого имеется встроенная функция loess, применение которой аналогично функции regress (листинг 13.11 и рис. 13.17):

loess (х, у, span) — вектор коэффициентов для построения регрессии данных отрезками полиномов;
interp(s,x,y,t) — результат полиномиальной регрессии:

s=loess(х,у,span);

х — вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;

у — вектор действительных данных значений того же размера;

span — параметр, определяющий размер отрезков полиномов (положительное число, хорошие результаты дает значение порядка span=0.75).

Параметр span задает степень сглаженности данных. При больших значениях span регрессия практически не отличается от регрессии одним полиномом (например, span=2 дает почти тот же результат, что и приближение точек параболой).

Листинг 13.11. Регрессия отрезками полиномов

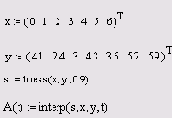
СОВЕТ

Регрессия одним полиномом эффективна, когда множество точек выглядит как полином, а регрессия отрезками полиномов оказывается полезной в противоположном случае.

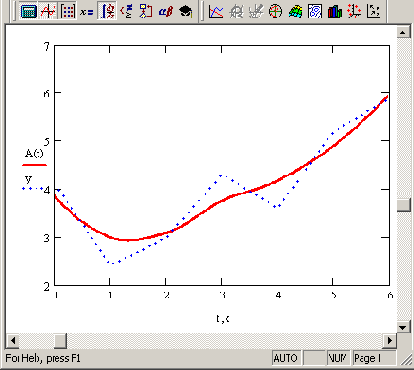
Рис. 13.17. Регрессия отрезками полиномов (продолжение листинга 13.11)

Двумерная полиномиальная регрессия

По аналогии с одномерной полиномиальной регрессией и двумерной интерполяцией (см. разд. 13.1.5), Mathcad позволяет приблизить множество точек Z_i,j(x_i,y_j) поверхностью, которая определяется многомерной полиномиальной зависимостью. В качестве аргументов встроенных функций для построения полиномиальной регрессии должны стоять в этом случае не векторы, а соответствующие матрицы.

regress (x,z,k) — вектор коэффициентов для построения полиномиальной регрессии данных.
loess (x, z, span) — вектор коэффициентов для построения регрессии данных отрезками полиномов.
interp(s,x,z,v) — скалярная функция, аппроксимирующая данные выборки двумерного поля по координатам х и у кубическими сплайнами.

s — вектор вторых производных, созданный одной из сопутствующих функций loess или regress.

х — матрица размерности Nx2, определяющая пары значений аргумента (столбцы соответствуют меткам х и у).

z — вектор действительных данных размерности N.

span — параметр, определяющий размер отрезков полиномов.

k — степень полинома регрессии (целое положительное число).

v — вектор из двух элементов, содержащий значения аргументов х и у, для которых вычисляется интерполяция.

ВНИМАНИЕ!

Для построения регрессии не предполагается никакого предварительного упорядочивания данных (как, например, для двумерной интерполяции, которая требует их представления в виде матрицы NxN). В связи с этим данные представляются как вектор.

Двумерная полиномиальная регрессия иллюстрируется листингом 13.12 и рис. 13.18. Сравните стиль представления данных для двумерной регрессии с представлением тех же данных для двумерной сплайн-интерполяции (см. листинг 13.6) и ее результаты с исходными данными (см. рис. 13.12) и их сплайн-интерполяцией (см. рис. 13.13).

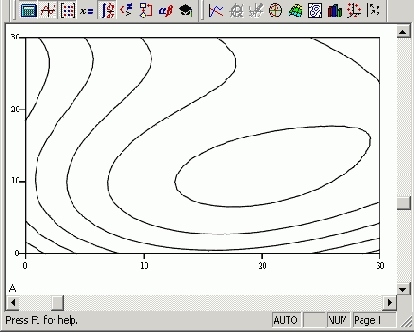
Рис. 13.18. Двумерная полиномиальная регрессия (продолжение листинга 13.12)

Листинг 13.12. Двумерная полиномиальная регрессия

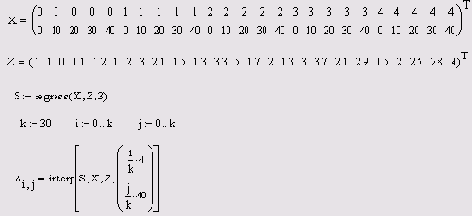
ПРИМЕЧАНИЕ

Обратите внимание на знаки транспонирования в листинге. Они применены для корректного представления аргументов (например, z, в качестве вектора, а не строки).

Содержание раздела