Математические задачи в пакете MathCAD 12
Глава 14.1.1. Фурье-спектр действительных данных
Преобразование Фурье имеет огромное значение для различных математических приложений, и для него разработан очень эффективный алгоритм, называемый БПФ (быстрое преобразование Фурье). Рассмотрим сначала наиболее типичную для физического эксперимента ситуацию расчета Фурье-спектра действительного сигнала, для которой алгоритм БПФ реализован в нескольких встроенных функциях Mathcad, различающихся нормировками:
- fft (у) — вектор прямого преобразования Фурье;
- FFT (у) — вектор прямого преобразования Фурье в другой нормировке:
- у — вектор действительных данных, взятых через равные промежутки значений аргумента.
ВНИМАНИЕ!
Аргумент прямого Фурье-преобразования, т. е. вектор у, должен иметь ровно
2n элементов (n— целое число). Результатом является вектор с
1+2n-1 элементами. Если число данных не совпадает со степенью
2, то необходимо дополнить недостающие элементы нулями, иначе вместо решения появится сообщение об ошибке.
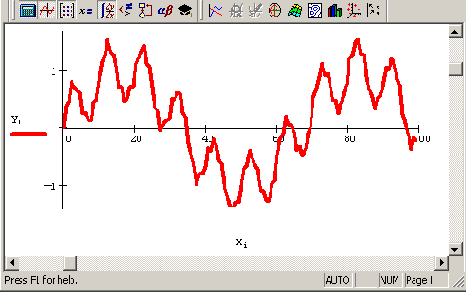
Рис. 14.1. Исходные модельные данные (продолжение листинга 14.1)
Чтобы смысл преобразования Фурье был более понятен, используем в качестве модельных данных дискретизацию детерминированного сигнала,, равного сумме трех синусоид (рис. 14.1). Листинг 14.1 демонстрирует расчет Фурье-спектра по
N=128 точкам, причем предполагается, что интервал дискретизации данных yi равен
Δ. В середине листинга применяется встроенная функция
fft, а его оставшаяся часть предназначена для корректного пересчета соответствующих значений частот
Ωi (они вычисляются в последней строке листинга). Обратите внимание, что результаты расчета представляются в виде модуля Фурье-спектра (рис. 14.2), поскольку сам спектр является комплексным. Очень полезно сравнить полученные амплитуды и местоположение пиков спектра (рис. 14.3) с определением синусоид в листинге 14.1.
Листинг 14.1. Быстрое преобразование Фурье
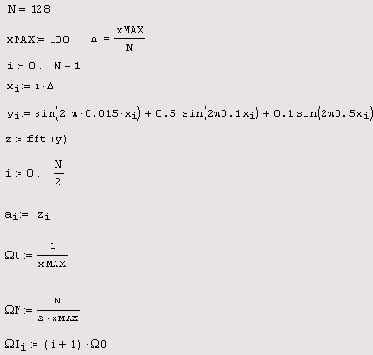
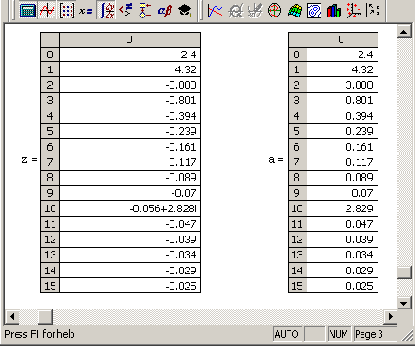
Рис. 14.2. Матрица-результат вычисления Фурье-спектра данных (продолжение листинга 14.1)
Исключительно важными представляются два параметра, заданные в предпоследней строке листинга 14.1, называемые соответственно граничной частотой и частотой Найквиста. Граничная частота
Ω0 определяет нижнюю, а частота Найквиста
ΩN — верхнюю границу аргумента вычисленного спектра, как показано маркерами на рис. 14.3. Кроме того, важно, что интервал дискретизации Фурье-спектра также равен
Ω0, а общее число вычисляемых
точек спектра составляет N/2 (в нашем примере N/2=64). Последние утверждения иллюстрируются маркерами на рис. 14.4, изображающем график Фурье-спектра вблизи нижней границы частот.
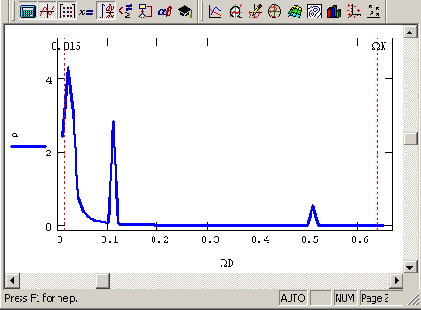
Рис. 14.3. График Фурье-спектра данных (продолжение листинга 14.1)
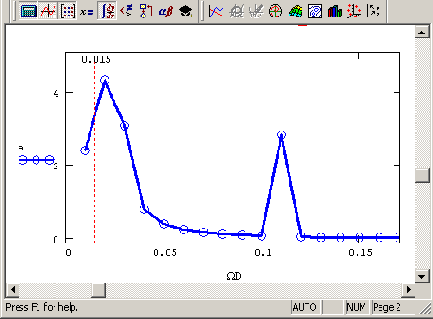
Рис. 14.4. Низкочастотная область Фурье-спектра (продолжение листинга 14.1)