Глава 14.1.4. Пример: артефакты дискретного Фурье-преобразования

При численном нахождении преобразования Фурье следует очень внимательно относиться к таким важнейшим параметрам, как объем выборки (в терминах листинга 14.1, xМАХ) и интервал дискретизации (Δ). Соотношение этих двух величин определяет диапазон частот (Ω_0,Ω_N), для которых возможно вычисление значений Фурье-спектра. В этой связи хотелось бы обратить внимание на три типичные опасности, которые могут подстерегать неподготовленного исследователя при расчете дискретного Фурье-преобразования и быть для него весьма неожиданными.

Влияние конечности интервала выборки

Во-первых, следует обратить внимание на само определение преобразования Фурье как интеграла с бесконечными пределами. Его численное отыскание подразумевает принципиальную ограниченность интервала интегрирования (просто в силу конечности объема выборки). Поэтому самым очевидным несоответствием будет поиск, вообще говоря, другого интеграла, отличного от интеграла Фурье. Влияние конечности интервала выборки проявляется главным образом на искажении его низкочастотной области. В качестве примера приведем Фурье-спектр гармонической функции с частотой 0.015. Для его расчета достаточно заменить в листинге 14.1 четвертую строку на равенство y_i:=sin(2π0.915x_i). Соответствующий Фурье-спектр изображен на рис. 14.7 (сверху — в обычном, а снизу — в более крупном масштабе) и демонстрирует не совсем правильное поведение в низкочастотной области. Как видно, спектр содержит довольно широкий максимум вместо одиночного пика, как было в случае средних частот сигнала на рис. 14.3.

ПРИМЕЧАНИЕ 1

Если быть точным, вместо спектра некоторой функции f (х) дискретное преобразование Фурье подразумевает вычисление спектра другой функции f (х)Ф(х), где Ф(х) — это функция-ступенька, равная единице в пределах расчетного интервала и нулю за его пределами. В частотной области это соответствует операции свертки означенных двух функций, что, конечно, искажает (неизвестный) точный спектр f (х). Для борьбы с проявлением конечности интервала выборки используются специальные методы, основанные на применении техники спектральных окон.

ПРИМЕЧАНИЕ 2

Из сказанного ясно, почему исследователя не должна смущать необходимость дополнения массива исходных данных нулями до размера 2" (чтобы можно было использовать алгоритм БПФ). По самому определению дискретного Фурье-преобразования, исходная функция и так предполагается равной нулю за пределами расчетного интервала, что приводит к неминуемым искажениям.

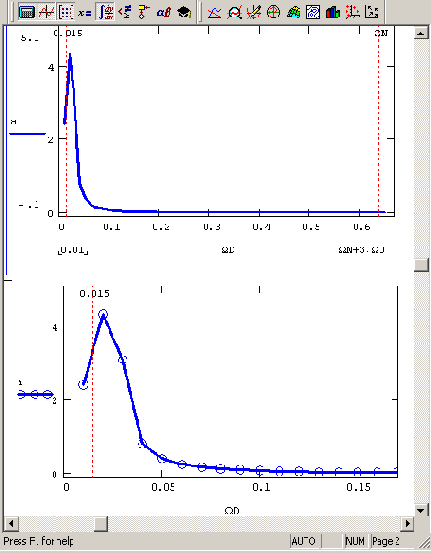
Рис. 14.7. Иллюстрация влияния конечности выборки на расчет низкочастотной части Фурье-спектра

Сдвиг ноль-линии

Еще одним, наиболее ярким, проявлением вредного влияния конечности интервала выборки может служить расчет Фурье-преобразования суммы гармонического сигнала и константы (рис. 14.8). Для того чтобы получить данный рисунок, достаточно еще слегка (по сравнению с рис. 14.7) модифицировать строку листинга, касающуюся определения компонент вектора у, добавив к нему i: y_i:=sin(2π0.915x_i)+1.

Сравнивая рис. 14.7 и 14.8, несложно догадаться, почему так разительно изменился вид спектра в низкочастотной области. Пугающий рост спектра на левом крае частотного интервала объясняется совокупностью двух факторов: конечности выборки и добавлением к сигналу ненулевой постоянной составляющей (так называемым сдвигом ноль-линии). Сумма сигнала и константы определяет соответствующее влияние на вычисленный спектр, который также оказывается (просто в силу линейности операции интегрирования) суммой спектров сигнала и ступенчатой функцией (равной той самой константе внутри расчетного интервала и нулю за его пределами).

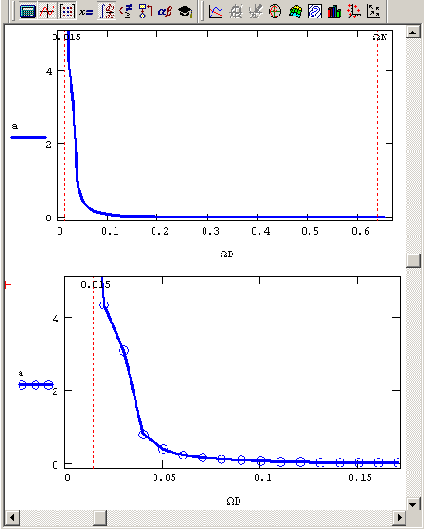
Рис. 14.8. Фурье-спектр суммы гармонического сигнала и константы (влияние конечности выборки)

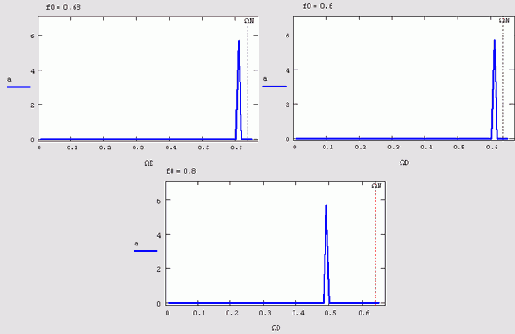
Рис. 14.9. Расчеты Фурье-спектров гармонических сигналов с разной частотой ("маскировка частот")

Избавиться от искажений, вызванных сдвигом ноль-линии, довольно просто. Достаточно (до Фурье-преобразования) вычислить среднее значение выборки и затем вычесть его из каждого элемента выборки. Если после этой операции вычислить Фурье-спектр, то он окажется примерно таким, как показано на рис. 14.7.

Маскировка частот

Еще один классический пример ошибочного расчета Фурье-спектра связан с возможным присутствием в сигнале гармоник с частотой, превышающей частоту Найквиста, в данном примере Ω_N=0.б4 (см. разд. 14.1.Г). Иллюстрация эффекта, называемого "маскировкой частот", приведена на рис. 14.9, который содержит расчет спектров трех различных синусоидальных сигналов с разной частотой f0. Первый спектр сигнала с частотой, меньшей частоты Найквиста, вычислен верно, а вот два остальных спектра показывают, что в случае превышения частоты Найквиста в спектре начинают присутствовать "лишние" пики. Появление артефактов спектра связано с тем, что дискретных отсчетов начинает не хватать для того, чтобы прописать высокочастотные гармоники с достаточной информативностью.

ПРИМЕЧАНИЕ

Напоминаем, что все листинги, имеющиеся в книге, а также документы Mathcad с расчетами всех рисунков, вы найдете на прилагаемом компакт-диске.

Содержание раздела