Математические задачи в пакете MathCAD 12
Глава 14.1.5. Пример: спектр модели сигнал/шум
Пока мы использовали в качестве примера детерминированный сигнал, представляющий собой сумму трех синусоид. Несмотря на единство термина "дискретное преобразование Фурье", прикладное применение спектрального анализа можно довольно четко разделить на две категории.
- Сигнал, подвергающийся спектральному анализу, получен в условиях пренебрежимо малой погрешности, т. е. его можно, фактически, считать детерминированным. Такая ситуация характерна для экспериментальной оптики и (разного рода) спектроскопии. В этом случае для большинства задач анализа сигналов бывает вполне достаточно использовать простые спектры Фурье, рассмотренные выше (см. разд. 14.1.1—14.1.3).
- Сигнал, полученный в присутствии значительной шумовой компоненты, которая существенно искажает его структуру. В этом случае следует говорить о смеси (к счастью, чаще всего аддитивной) "полезный сигнал + шум", причем в большинстве случаев заранее известна некоторая информация о статистике шумовой компоненты. Данная ситуация очень часто встречается в экспериментальной геофизике и радиофизике. В этом случае подходить к интерпретации спектров следует с вероятностной точки зрения. Как раз этому вопросу мы и посвятим данный пример.
Фурье-спектр
Внесем минимальное добавление в расчеты листинга 14.1, а именно добавим к его четвертой строке (в которой определяется
yi) еще одно (четвертое) слагаемое: псевдослучайную величину
σrnd(1), где значение 1/σ характеризует отношение сигнал/шум. Явный вид изменений, которые следует внести в листинг 14.1, приведен на рис. 14.10, наряду с графиком сигнала
у(х). Расчет Фурье-спектра данного сигнала (в соответствии с алгоритмом, представленным выше, см. листинг 14.1) показан на рис. 14.11. Как видно, присутствие шумовой компоненты может значительно искажать спектр сигнала и затруднять его интерпретацию.
ПРИМЕЧАНИЕ
Максимальное значение спектра на левом крае частотного интервала является ни чем иным, как проявлением искажающего влияния конечности выборки и сдвига ноль-линии (см. разд. 14.1.3), произошедшим из-за внесения шума с математическим ожиданием, равным
0.5.
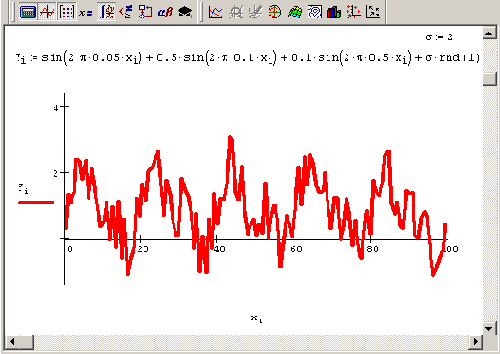
Рис. 14.10. Модель сигнал / шум
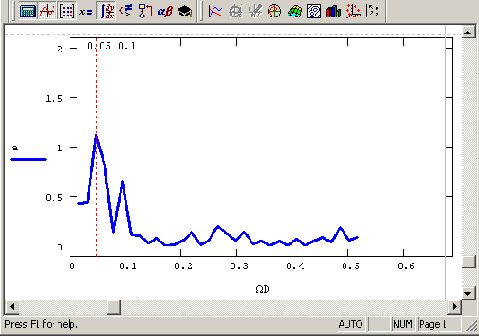
Рис. 14.11. График Фурье-спектра данных
Спектр мощности
В силу стохастичности исходных данных, представляющих сумму полезного сигнала и шума, сами вычисленные значения спектра Фурье носят также случайный характер. В этой связи необходимо знать, с какой погрешностью они рассчитываются. Однако из курса математической статистики известно, что для обычного Фурье-преобразования случайного сигнала (в частности, нормального) не найдено оценок для погрешности. Это слабое место Фурье-спектров делает их практически неприменимыми для анализа случайных сигналов, а вместо них надо применять так называемые спектры мощности (или, по-другому, энергетические спектры), для которых указанные оценки существуют.
Не углубляясь в теорию математической статистики, приведем пример вычисления спектра мощности сигнала (рис. 14.10), основанный его определении. Как известно, спектром мощности сигнала называют Фурье-преобразование его корреляционной функции. Таким образом, алгоритм расчета спектра мощности сводится к следующему: во-первых, вычислению автокорреляционной функции (рис. 14.12); во-вторых, ее прореживанию и (или) сглаживанию (в целях уменьшения влияния конечности выборки); и, наконец, в-третьих, расчету ее Фурье-преобразования. Результат вычисления спектра мощности (листинг 14.3) в соответствии с приведенным сценарием показан на рис. 14.13.
ПРИМЕЧАНИЕ 1
Аналогичным образом, через Фурье-преобразование взаимной корреляционной функции, определяются взаимные спектры мощности двух выборок.
ПРИМЕЧАНИЕ 2
Еще один способ вычисления спектров мощности, не требующий расчета функции корреляции, приведен ниже (см. разд. 14.3.6).
ПРИМЕЧАНИЕ 3
Методика расчета в Mathcad корреляционной функции случайного процесса обсуждалась в главе 12 (см. разд. 12.3.3).
Листинг 14.3. Расчет спектра мощности для модели сигнал/шум
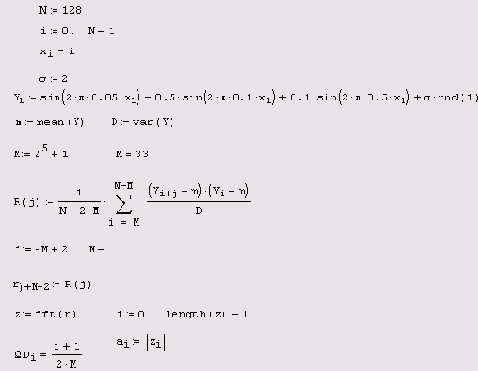

Рис. 14.12. Автокорреляционная функция
модельной зависимости сигнал / шум
(продолжение листинга 14.3)
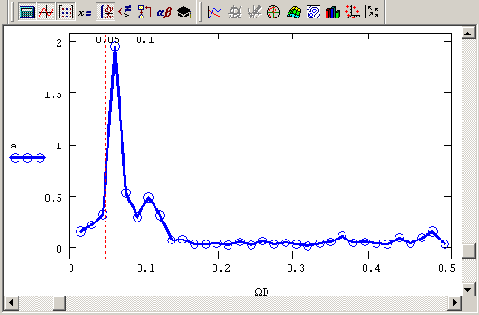
Рис. 14.13. График спектра мощности данных
модельной зависимости сигнал / шум
(продолжение листинга 14.3)