Математические задачи в пакете MathCAD 12
Глава 14.3.5. Спектральная фильтрация
Альтернативой всем представленным до сих пор алгоритмам, в частности, методу полосовой фильтрации (см. предыдущий разд.) является фильтрация на основе интеграла Фурье. Пока мы использовали для подавления в сигнале тех или иных частотных диапазонов определенные процедуры, основанные на арифметических преобразованиях. Между тем, для той же цели (правда, с большими вычислительными затратами) можно применять методы Фурье-анализа. Действительно, если вычислить спектр сигнала, удалить из него (или существенно уменьшить) определенные частоты, а затем выполнить обратное преобразование Фурье, то результатом будет фильтрованный сигнал.
Пример фильтрации на основе преобразования Фурье приведен в листинге 14.11. В качестве модельного сигнала использовалась смесь двух гармонических сигналов и равномерно распределенного шума (рис. 14.24). Фурье-спектр данных
z, вычисленный при помощи встроенной функции fft, показан на рис. 14.25. Листинг 14.11 отличается от листинга 14.1 (см. разд. 14.1. Г), главным образом, последними двумя строками, в которых, собственно, и определяется явный вид спектрального фильтра
w(Ω), или, по-другому, спектральное окно. Обратное Фурье-преобразование спектра произведения спектрального окна
w(Ω) и Фурье-спектра сигнала
z, представляющее собой результат фильтрации, показано на рис. 14.24 сплошной кривой.
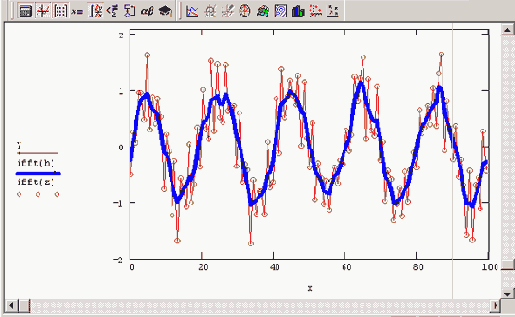
Рис. 14.24. Исходный модельный сигнал (кружки)
и результат его фильтрации на основе Фурье-преобразования
(продолжение листинга 14.11)
Листинг 14.11. Фильтрация на основе преобразования Фурье
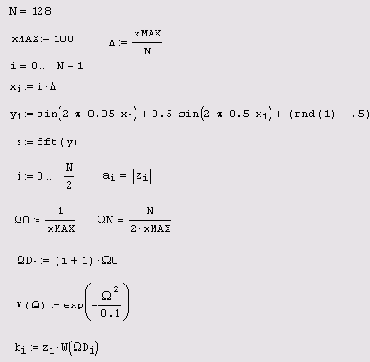
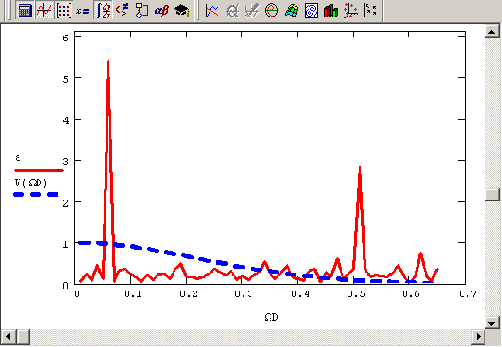
Рис. 14.25. Фурье-преобразование модельного сигнала
и спектральное окно-фильтр
(продолжение листинга 14.11)